又称正轴等角圆柱投影。圆柱投影的一种，由荷兰地图学家墨卡托（G. Mercator）于1569年创拟。为地图投影方法中影响最大的。
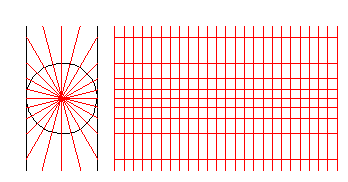
设想一个与地轴方向一致的圆柱切于或割于地球，按等角条件将经纬网投影到圆柱面上，将圆柱面展为平面后，得平面经纬线网。投影后经线是一组竖直的等距离平 行直线，纬线是垂直于经线的一组平行直线。各相邻纬线间隔由赤道向两极增大。一点上任何方向的长度比均相等，即没有角度变形，而面积变形显著，随远离标准 纬线而增大。该投影具有等角航线被表示成直线的特性，故广泛用于编制航海图和航空图等。
墨卡托投影在切圆柱投影与割圆柱投影中，最早也是最常用的是切圆柱投影。

 

(http://baike.baidu.com/view/301981.htm)

 

公式参数

 

a -- 椭球体长半轴

b -- 椭球体短半轴

f -- 扁率 (a-b) /a

e -- 第一偏心率  

e’-- 第二偏心率  

N -- 卯酉圈曲率半径

 

R -- 子午圈曲率半径

 

B -- 纬度，L -- 经度，单位弧度(RAD)

 -- 纵直角坐标,  -- 横直角坐标，单位米(M)

 

椭球体参数

我国常用的3 个椭球体参数如下（源自“全球定位系统测量规范 GB/T 18314-2001”）：

 

椭球体	长半轴 a（米）	短半轴b（米）
Krassovsky（北京54 采用）	6378245	6356863.0188
IAG 75（西安80 采用）	6378140	6356755.2882
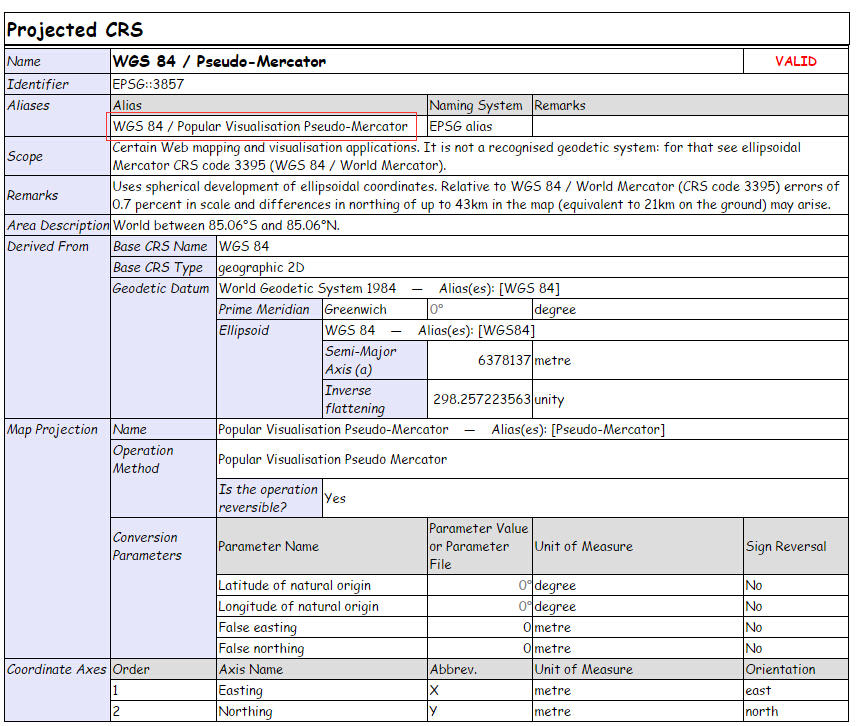
WGS 84	6378137	6356752.3142

 

 

墨卡托投影正反解公式

墨卡托投影正解公式：（B,L）→(X,Y)，标准纬度B0，原点纬度 0，原点经度L0

 

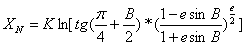
墨卡托投影反解公式：(X,Y) →（B,L），标准纬度B0，原点纬度 0，原点经度L0

 

 

公式中EXP 为自然对数底，纬度B 通过迭代计算很快就收敛了。

 

程序实现

 

投影的实现封装于一个类class MercatorProj中。

类中定义若干私有变量，保存相关参数

 

 int __IterativeTimes;      //反向转换程序中的迭代次数
double __IterativeValue;  //反向转换程序中的迭代初始值
double __A;    //椭球体长半轴,米
double __B;    //椭球体短半轴,米
double __B0; //标准纬度,弧度
double __L0; //原点经度,弧度

 

以上参数的设定由如下几个public函数完成

//设定__A与__B
void MercatorProj::SetAB(double a, double b)
{if(a<=0||b<=0){return;}__A=a;__B=b;
}
//设定__B0
void MercatorProj::SetB0(double b0)
{if(b0<-PI/2||b0>PI/2){return;}__B0=b0;
}
//设定__L0
void MercatorProj::SetL0(double l0)
{if(l0<-PI||l0>PI){return;}__L0=l0;
}
//构造函数中赋予参数默认值
MercatorProj::MercatorProj()
{__IterativeTimes=10;     //迭代次数为10__IterativeValue=0;        //迭代初始值__B0=0;__L0=0;__A=1;__B=1;
}/*******************************************
投影正向转换程序
double B: 维度,弧度
double L: 经度,弧度
double& X:     纵向直角坐标
double& Y:      横向直角坐标
*******************************************/
int MercatorProj::ToProj(double B, double L, double &X, double &Y)
{double f/*扁率*/,e/*第一偏心率*/,e_/*第二偏心率*/,NB0/*卯酉圈曲率半径*/,K,dtemp;double E=exp(1);if(L<-PI||L>PI||B<-PI/2||B>PI/2){return 1;}if(__A<=0||__B<=0){return 1;}f =(__A-__B)/__A;dtemp=1-(__B/__A)*(__B/__A);if(dtemp<0){return 1;}e= sqrt(dtemp);dtemp=(__A/__B)*(__A/__B)-1;if(dtemp<0){return 1;}e_= sqrt(dtemp);NB0=((__A*__A)/__B)/sqrt(1+e_*e_*cos(__B0)*cos(__B0));K=NB0*cos(__B0);      Y=K*(L-__L0);X=K*log(tan(PI/4+B/2)*pow((1-e*sin(B))/(1+e*sin(B)),e/2));return 0;
}
/*******************************************
投影反向转换程序
double X: 纵向直角坐标
double Y: 横向直角坐标
double& B:     维度,弧度
double& L:     经度,弧度
*******************************************/
int MercatorProj::FromProj(double X, double Y, double& B, double& L)
{double f/*扁率*/,e/*第一偏心率*/,e_/*第二偏心率*/,NB0/*卯酉圈曲率半径*/,K,dtemp;double E=exp(1);if(__A<=0||__B<=0){return 1;}f =(__A-__B)/__A;dtemp=1-(__B/__A)*(__B/__A);if(dtemp<0){return 1;}e= sqrt(dtemp);dtemp=(__A/__B)*(__A/__B)-1;if(dtemp<0){return 1;}e_= sqrt(dtemp);NB0=((__A*__A)/__B)/sqrt(1+e_*e_*cos(__B0)*cos(__B0));K=NB0*cos(__B0);      L=Y/K+__L0;B=__IterativeValue;for(int i=0;i<__IterativeTimes;i++){B=PI/2-2*atan(pow(E,(-X/K))*pow(E,(e/2)*log((1-e*sin(B))/(1+e*sin(B)))));}return 0;
}

另需几个常量和函数：

//圆周率
const double PI=3.1415926535897932;
//角度到弧度的转换
double DegreeToRad(double degree)
{return PI*((double)degree/(double)180);            
}
//弧度到角度的转换
double RadToDegree(double rad)
{return (180*rad)/PI;            
}测试主函数：double b0,l0;double latS,lgtS,latD,lgtD;b0=30;l0=0;latS=60;lgtS=120;m_mp.SetAB(6378137, 6378245,6378140); // WGS 84m_mp.SetB0(DegreeToRad(b0));m_mp.SetL0(DegreeToRad(l0));m_mp.ToProj(DegreeToRad(latS),DegreeToRad(lgtS),latD,lgtD);cout<< latD<<”:”<< lgtD<<endl;
// 7248377.351067:11578353.630128latS=123456;lgtS=654321;m_mp.FromProj(latS,lgtS,latD,lgtD);latD=RadToDegree(latD);lgtD=RadToDegree(lgtD);cout<< latD<<”:”<< lgtD<<endl;
// 1.288032: 6.781493

参考材料： 

1、《常用地图投影转换公式》 青岛海洋地质研究所 戴勤奋

2、百度百科

 

 原文链接：墨卡托投影实现