废话
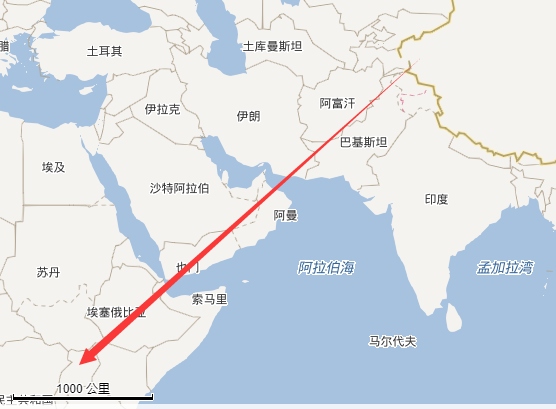
为啥一堆人都说墨卡托投影是从圆心向圆柱面发射线, 反正我觉得不是那样, 不然公式显然就不对了(也可能是我马虎), 后来去wiki查了一下, 找到了公式的推导.
公式
x = R ( λ − λ 0 ) , y = R ln [ tan ( π 4 + φ 2 ) ] . {\displaystyle x=R(\lambda -\lambda _{0}),\qquad y=R\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\varphi }{2}}\right)\right].} x=R(λ−λ0),y=Rln[tan(4π+2φ)].
其中 λ \lambda λ是经度, ϕ \phi ϕ是纬度(即投影前的坐标); x , y x,y x,y是投影后的坐标; R R R是球的半径; λ 0 \lambda_0 λ0是y轴所在经度
大概感觉是这样(即废话里说的)(但是这个不精确, 不然公式就不是这样了):
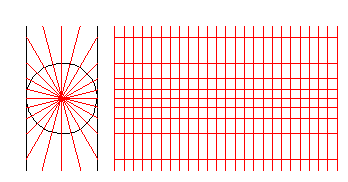
左图为侧视图, 中间的球就是原来的坐标系, 两个竖线代表了一个圆柱, 是投影后的坐标系. 右图是圆柱展开后, 最终的坐标系.
赤道成为 x x x轴, 并且在x轴上(经度与x坐标)是成比例的(这个是标准的