实验原理及内容

说明：这部分内容主要包括：

1、形式化描述实验中所使用的数据结构和存储结构，给出函数之间的调用关系和数据传递方式；

2、给出核心算法的C++或Java等语言的源代码，并加上详细注释，分析算法的时间复杂度；

3、给出测试数据及运行结果、实验相关结论等。

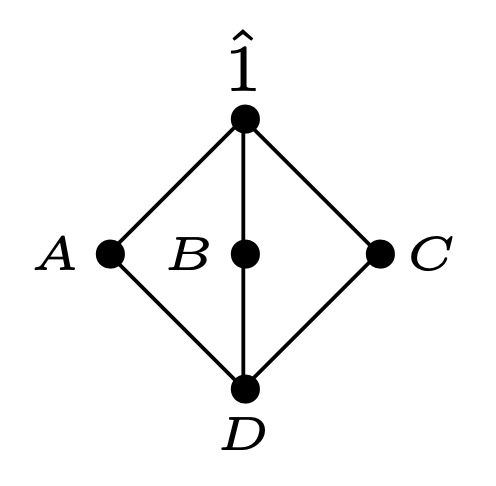
这次题目要求是根据整除关系建立偏序关系，集合由一个正整数的因子所构成，所以该偏序集中的最大下界为1，最小上界为该正整数，所以该偏序集是一个格。又因为是整除关系，则“交”即为求两者的最大公约数，“并”即为求两者的最小公倍数，故而满足分配律，因此这个偏序集是个分配格。

判断这个集合是否为有补格，根据定理可以先判断元素数是否为2的倍数，不过编程起来更加复杂，于是我就采用逐个求补元的方法。如果对于某个元素找完了所有的元素也没找到补元，则不满足有补性，否则就为有补格，又因为是分配格，所以也是布尔格。 

对于所有可能的偏序集，有一个特例即{1}，这个偏序集最小上界等于最大下界等于1，1的补元是他本身。他也是个有补格，要特殊考虑。

 

#include <iostream>
#include <cstdlib>
#include <string>
using namespace std;
//辗转相除法求最大公约数 
int GYS(int a ,int b)
{int temp;if(a<b){temp=a;a=b;b=temp;
}
while(temp=a%b)
{a=b;b=temp;
};
return b;
};
//根据最大公约数求最小公倍数 
int GBS(int a,int b)
{return a*b/GYS(a,b);
};
int main()
{int n,m,i,j,k;int a[20];a[0]=1;//第一个元素肯定是1 j = n = 1;//j代表数组a[]的下标，n标记元素个数 //do{cout<<"请输入一个正整数：";cin>>m;for(i=2;i<=m/2;i++)//求给定正整数的因子：{if(m%i==0){//若是能被给定正整数整除，即加入数组a[]   a[j++]=i;n++;}}if(m!=1){//最后把该正整数加入数组a[]，1不重复加入  a[j]=m;n++;}cout<<"因子有：";for(i=0;i<n;i++){cout<<a[i]<<" ";}cout<<endl;int flag=0;for(i=0;i<n;i++){for(j=n-1;j>=0;j--){if(GBS(a[i],a[j])==m && GYS(a[i],a[j])==1){cout<<a[i]<<"有补元素"<<a[j]<<"。\n";break;}if(j==0){flag=1;}}}if(!flag){cout<<"因为所有成员都有补元素，所以这是一个有补格。"<<endl;}else{cout<<"因为不是所有成员都有补元素，所以不是一个有补格。"<<endl;}flag=0;//已知肯定是分配格， 这里只是进一步确信，flag标记是否有反例for(i=0;i<n;i++){for(j=0;j<n && j!=i;j++){for(k=0;k<n && k!=j && j!=i;k++){if(GYS(a[i],GBS(a[j],a[k]))!=GBS(GYS(a[i],a[j]),GYS(a[i],a[k]))){flag=1;cout<<"因为"<<a[i]<<"∧("<<a[j]<<"∨"<<a[k]<<")!=("<<a[i]<<"∧"<<a[j]<<")∨("<<a[i]<<"∧"<<a[k]<<"),所以这不是一个布尔格。\n";//验证a∧(b∨c)==(a∧b)∨(a∧c) break;}if(GBS(a[i],GYS(a[j],a[k]))!=GYS(GBS(a[i],a[j]),GBS(a[i],a[k]))){flag=1;cout<<"因为"<<a[i]<<"∨("<<a[j]<<"∧"<<a[k]<<")!=("<<a[i]<<"∨"<<a[j]<<")∧("<<a[i]<<"∨"<<a[k]<<"),所以这不是一个布尔格。\n";//验证a∨(b∧c)==(a∨b) ∧ (a∨c) break;}}if(flag)break;
}if(flag){break;}if(!flag){cout<<"因为所有成员都满足分配性，所以这是一个分配格。\n";break;}
}
}

运行结果：

​​​​​​​