偏序关系的定义
偏序关系就是自反,反对称,传递的序偶集合。其中满足偏序的集合我们一般称为A,偏序关系一般称为R。
A*A产生的序偶有很多,所以我们使用<A,R>去表示满足某个偏序关系的A中元素的子集。
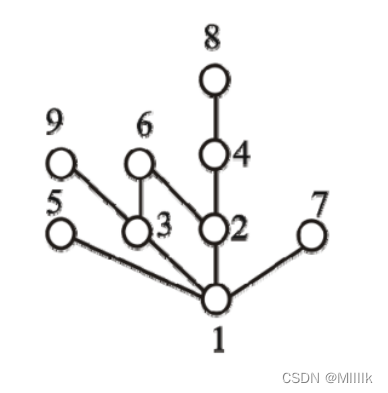
如果使用图像画这个偏序集的画一般使用哈斯图对图像进行化简:
被偏序的元素放在哈斯的底部,偏序的元素放在上层,自反的圆圈不画,箭头的指向也不画,传递的图像也不画。
最大元如何确定
最大元的定义:最大元定义的意思是:是否存在一个元素,使得其他的元素都与其是偏序关系
注意这里的定义是“一个元素”,也就是说如果有存在两个元素对其他所有元素都有偏序关系,那么就不存在最大元。当然这只是一个为了方便的说法,如果要深究一下应该是这样的,我们从偏序关系的定义出发,自反,反对称,传递,其实这样的关系定义,我们在画图的时候注定就是一个树形结构的图形,所以将偏序关系的哈斯图对应到现实生活的话,就是几个步骤的连续执行。最大元的意思就是是否存在一个最终的目标。
最小元的定义:最小元定义的意思是:是否存在一个元素,使得它与其他元素都形成被偏序关系
什么是被偏序关系?,被偏序关系就是反的偏序关系,比如2被1整除,那么1整除2就是差不多这样的一个东西。如果将定义理解为现实生活的例子就是在一系列的步骤中,是否唯一存在一个起点去作为其他步骤的延申。
极大元的定义是:是否存在这样的元素,若有一个元素与其形成偏序关系,那么这个元素只能是自己
上面的最大元强调的是唯一元素,而这里的极大元强调只有自己是自己的偏序关系对象,也就是说只要满足这个条件就是一个极大元,那么假设一个哈斯图最终有两个终结点,所以这个哈斯图并没有最大元,但是因为这两个终结点都是可以与其他元素组成偏序关系,所以这两个终结点就是两个极大元。
极小元的定义是:是否存在这样的元素,若有一个元素与其形成被偏序关系,那么这个元素只能是自己
极小元的定义和最大元的定义其实是类似的。就比如一个哈斯图有两个起点,只有自己是自己的被偏序关系对象,那么这个元素就是一个极小元
我们发现极大和极小元并不考虑不能够对比的情况,最大和最小元都需要能够对集合B(集合A的子集)都具备偏序关系或者被偏序关系。所以就经常会出现最大元和最小元都不存在的情况,但是极小元以及极大元主要考虑是是否有其他的元素可以与其组成偏序关系或者被偏序关系,如果没有那么它就是极小或者极大元,所以这就是为什么在哈斯图上的单独节点又是极大元也是极小元。
如果用方便的视角想要直接找出极小元和极大元,比如要找极大元,就看它上面还有没有元素与其相连,如找极小元就看它下面有没有元素与其相连。
如果找最大元,就看有没有唯一的最终目的点,如果找最小元就看有没有唯一的起始点。
上界与上确界如何找
只要属于A元素的其中一个元素对集合B任意的元素都有偏序关系,那么就称这个元素是一个上界元素
上界元素中第一个出现的,或者说最小的称为上确界

我们来分析一下上面的几个题目:
第一个{6,12},因为12,24,36都与6和12具备整除的关系,所以12,24,36都是上界元素,因为12是最先出现,最小的,所以它是上确界
第二个{2,3},因为2或者3都不能满足与{2,3}中的任意元素有整除关系,所以2与3不是上界元素,但是6,12,24,36都与{2,3}又整除关系,所以它们都是上界元素,因为6是最先出现,最小的,所以它是上确界
第三个无,因为24和36都不能与{24,36}中的任意元素有整除关系,所以24和36不是上界元素,而且24和36的上面已经没有任何的元素了,这就意味着没有任何元素与24或者36有偏序关系,所第三个例子就没有任何的上界元素,因为没有任何上界元素,所以就没有任何上确界
第四个{2,3,6,12}和上面三个同理
下界与下确界如何找
只要属于A元素的其中一个元素对集合B任意的元素都有被偏序关系,那么就称这个元素是一个下界元素
下界元素中第一个出现,或者说最最大的就称为下确界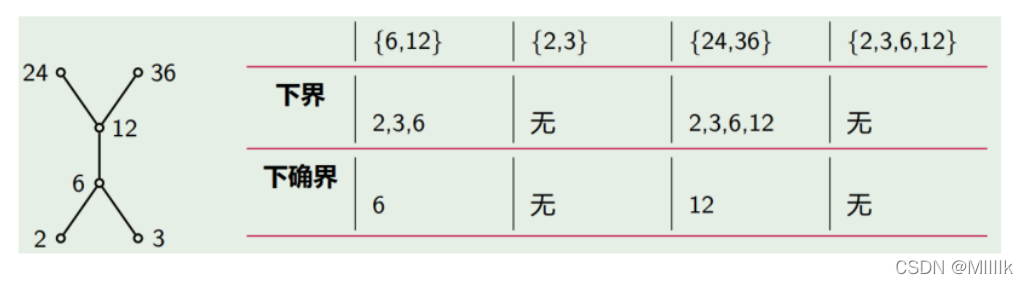
第一个{6,12},因为2,3,6与6和12都有被偏序关系,所以2,3,6都是下界元素,而且因为6是最先出现,而且是最大的下界元素,所以6是下确界
第二个无,因为2,3都不能与{2,3}中的任意元素有被偏序关系,所以说2和3都不是下界元素,因为没有下界元素,所以就没有下确界
其他两个同理
特殊的例题

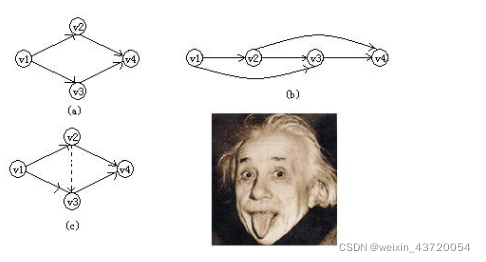
B{x1,x2}
B的最大元:因为在B中没有唯一的终点,所以B没有最大元
B的最小元:因为B中没有唯一的起点,所以B没有最小元
B的极大元:因为B中的x1和x2不能与其他任何的元素有偏序关系,所以x1和x2就是两个极大元
B的极小元:因为B中的x1和x2不能与其他任何元素有被偏序关系,所以x1和x2就是两个极小元
B的上界:因为在上图中B中的元素上没有任何的元素与其有偏序关系,而且x1与x2之间也没有任何的偏序关系,所以x1与x2并不是上界元素,
B的下界:从上图可知x3与x4与x1和x2都有被偏序关系,所以x3和x4是B的下界元素。
B的下界元素是以同样的次序,都是最先出现的,所以B并没有下确界
C{x3,x4}
C与B同理