等价关系偏序关系全序关系

article/2025/8/27 16:49:04

等价关系

$A\neq \varnothing$ , 并且 $R\in A\times A$ , 如果 R是自反，对称，传递的，称R为A上的等价关系。

偏序关系

$A\neq \varnothing$ ，并且 $R\in A\times A$ ,

如果 R是自反: $xRx$ (每个元素都和自身有关系)；

反对称：如果有 $xRy,yRx$ ，则 $x=y$ ,否则 $xRy,yRx$ ，不能同时存在；

传递的：如果有 $xRy,yRz,$ 必须有 $xRz$ ;

称R为A上的偏序关系。使用 $\preceq$ 表示偏序关系，读作 ’小于等于‘

用公式表示 $<x,y>\in R\Leftrightarrow xRy\Leftrightarrow x\preceq y$

全序关系

设 R是集合 X 上的偏序关系，如果对于每个 x , y ∈ X ，必有 $xRy$ 或 $yRx$ ，则称 R 是集合 X 上的全序关系。

如果 a ≤ b 且 b ≤ a 则 a = b (反对称性)
如果 a ≤ b 且 b ≤ c 则 a ≤ c (传递性)
a ≤ b 或 b ≤ a (完全性)

一般的说偏序集合的两个元素 x 和 y可以处于四个相互排斥的关联中任何一个：要么 x < y，要么 x = y，要么 x > y，要么 x 和 y 是“不可比较”的（三个都不是）。全序集合是用规则排除第四种可能的集合：所有元素对都是可比较的，并且声称三分法成立。

直观上，偏序指集合上只有部分元素之间可比较，而全序是指全体元素均可比较。

（偏序只对部分元素成立关系R，全序对集合中任意两个元素都有关系R）

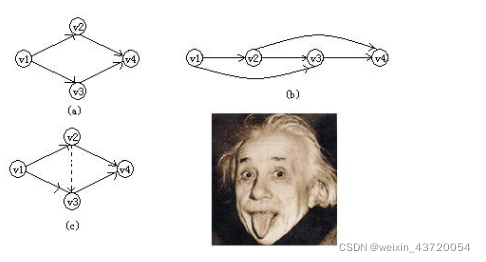
来看a图

按照正常遍历那么有2种路径，分别为124,134，2和3之间无法判断谁前谁后,而其他则可以判断前后顺序，比如1始终在2，3遍历之前。2和3始终在4之前

那2和3呢？无法判断，所以这就是偏序，此时2和3因没有顺序，整个是部分有序；再看图b在2和3之间加了一个指向，由2指向3，所以路线只有1234，

偏序只对部分元素成立关系R，全序对集合中任意两个元素都有关系R。
例如：
集合的包含关系就是半序，也就是偏序，因为两个集合可以互不包含；
而实数中的大小关系是全序，两个实数必有一个大于等于另一个；
又如：复数中的大小就是半序，虚数不能比较大小。

偏序关系与等价关系 ( 等价关系用于分类 | 偏序关系用于组织 )

1. 偏序关系是非常常用的二元关系 , 通常用来表示层次结构

2. 等价关系是用来分类的 , 将一个集合分为几个等价类

3. 偏序关系通常是用来组织的 , 在每个类的内部 , 赋予其一个结构 , 特别是层次结构 , 有上下层级