第四章终于结束了……接下来会休息一段时间，祝各位五一劳动节快乐！

……

想了想还是不休息了，继续继续！！

实时渲染（第四版）Real-Time Rendering (Fourth Edition)

第4章变换 Chapter 4 Transforms

4.5 变形 Morphing

在执行动画时，从一个三维模型变形到另一个三维模型可能会很有用 [28、883、1000、1005]。想象一下，一个模型在时间 $t_{0}$ 显示，我们希望它在时间 $t_{1}$ 变成另一个模型。对于介于 $t_{0}$ 和 $t_{1}$ 之间的所有时间，都使用某种插值获得了连续的“混合”模型。变形的一个例子如图 4.14 所示。

变形（Morphing）涉及解决两个主要问题，即顶点对应问题（the vertex correspondence problem）和插值问题（the interpolation problem）。给定两个任意模型，这些模型可能具有不同的拓扑（topologies），不同的顶点数量和不同的网格连接性，通常必须从建立这些顶点对应关系开始。这是一个困难的问题，并且在该领域已经进行了很多研究。我们推荐感兴趣的读者阅读 Alexa 的调查 [28]。

但是，如果两个模型之间已经存在一对一的顶点对应关系，则可以在每个顶点的基础上进行插值。也就是说，对于第一个模型中的每个顶点，在第二个模型中必须仅存在一个顶点，反之亦然。这使插值变得容易。例如，线性插值可以直接在顶点上使用（其他进行插值的方法请参见第 17.1 节）。

图4.14。顶点变形。为每个顶点定义了两个位置和法线。在每个帧中，中间位置和法线由顶点着色器线性插值。（图片由NVIDIA Corporation提供。）

为了计算时间 $t\;\epsilon\; [t0,\;t1]$ 的变形顶点，我们首先计算 $s=(t-t0)/(t_{1}-t_{0})$ ，然后进行线性顶点混合，

$\textbf{m}=(1-s)\textbf{p}_{0}+s\textbf{p}_{1},\;\;\;\;\;\;\;\;\;\;(4.60)$

其中 $\textbf{p}_{0}$ 和 $\textbf{p}_{1}$ 对应于同一顶点，但是在不同的时间， $t_{0}$ 和 $t_{1}$ 。

用户具有更直观控制的变形变体称为变形目标（morph targets）或混合形状（blend shapes） [907]。基本思想可以使用图 4.15 进行解释。

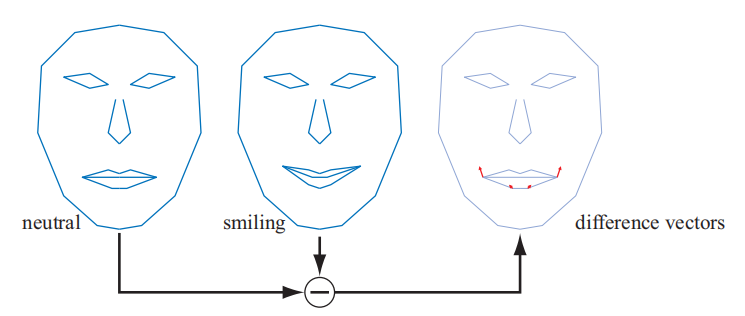
图4.15。在给定两个嘴部姿势的情况下，将计算一组差异向量以控制插值甚至外推。在变形目标中，差异向量用于将运动“添加”到中性面上。对于差异向量使用正权重，会露出笑容，而负权重会产生相反的效果。

我们从一个中性模型开始，在这种情况下，它是一张脸。让我们用 $N$ 表示该模型。此外，我们还有一组不同的脸部姿势。在示例中只有一个姿势，即一张笑脸。通常我们可以允许 $k\geqslant 1$ 个不同的姿势，表示为 $P_{i},\;i\;\epsilon\; [1,\;...\;,\;k]$ 。作为预处理，“差异面”的计算公式为： $D_{i}=P_{i}-N$ ，即，从每个姿势中减去中性模型。

在这一点上，我们有一个中性模型 $N$ 和一组差异姿势 $D_{i}$ 。然后可以使用以下公式获得变形模型 M： $M=N+\sum ^{k}_{i=1}w_{i}D_{i}.\;\;\;\;\;\;\;\;\;\;(4.61)$

这是中性模型，最重要的是，我们使用权重 $w_{i}$ 添加所需的不同姿势的特征。对于图 4.15，设置 $w_{1}=1$ 可使我们恰好位于插图中间。使用 $w_{1}=0.5$ 给我们一个半张微笑的脸，依此类推。你可以使用负权重，也可以使用大于 1 的权重。

对于这个简单的脸部模型，我们可以添加另一只眉毛“悲伤”的脸。负重的眉毛会产生“快乐”的眉毛。由于位移是累加的，因此该眉毛姿势可与笑脸姿势一起使用。

变形目标（Morph targets）是一种强大的技术，可为动画师提供很多控制，因为模型的不同特征可以独立于其他特征进行操纵。Lewis 等。[1037] 引入了姿势空间变形，它结合了顶点融合和顶点变形目标。Senior [1608]使用预先计算的顶点纹理来存储和检索目标姿势之间的位移。支持流输出的硬件和每个顶点的 ID 允许在单个模型中使用更多目标，并且可以在GPU上专门计算效果[841，1074]。使用低分辨率网格，然后通过细分阶段和位移映射生成高分辨率网格，可以避免在高度详细的模型中为每个顶点蒙皮的成本 [1971]。

图 4.16。角色 Delsin 在《声名狼藉:私生子(inFAMOUS:Second Son)》中的脸部使用混合形状进行了动画处理。所有这些拍摄都使用相同的静止姿势面孔，然后修改不同的权重以使面孔看起来有所不同。（图像由 Naughty Dog LLC 提供。inFAMOUS Second son c 2014 Sony Interactive EntertainmentLLC。inFAMOUS Second Son 是 Sony Interactive Entertainment LLC 的商标。由 Sucker Punch Productions LLC开发。）

图 4.16 显示了同时使用蒙皮和变形的真实示例。Weronko 和 Andreason [1872]在《教团 : 1886 (The Order : 1886)》中使用了蒙皮和变形。

引用：

[28] Alexa, Marc, “Recent Advances in Mesh Morphing,” Computer Graphics Forum, vol. 21, no. 2, pp. 173–197, 2002. Cited on p. 87, 88, 102

[883] Kent, James R., Wayne E. Carlson, and Richard E. Parent, “Shape Transformation for Polyhedral Objects,” Computer Graphics (SIGGRAPH ’92 Proceedings), vol. 26, no. 2, pp. 47–54, 1992. Cited on p. 87

[1000] Lazarus, F., and A. Verroust, “Three-Dimensional Metamorphosis: A Survey,” The Visual Computer, vol. 14, no. 8, pp. 373–389, 1998. Cited on p. 87, 102

[1005] Lee, Aaron W. F., David Dobkin, Wim Sweldens, and Peter Schr¨oder, “Multiresolution mesh morphing,” in SIGGRAPH ’99: Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques, ACM Press/Addison-Wesley Publishing Co., pp. 343– 350, 1999. Cited on p. 87

[28] Alexa, Marc, “Recent Advances in Mesh Morphing,” Computer Graphics Forum, vol. 21, no. 2, pp. 173–197, 2002. Cited on p. 87, 88, 102

[907] Kleinhuis, Christian, “Morph Target Animation Using DirectX,” in Wolfgang Engel, ed., ShaderX4, Charles River Media, pp. 39–45, 2005. Cited on p. 89

[1037] Lewis, J. P., Matt Cordner, and Nickson Fong, “Pose Space Deformation: A Unified Approach to Shape Interpolation and Skeleton-Driven Deformation,” in SIGGRAPH ’00: Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, ACM Press/Addison-Wesley Publishing Co., pp. 165–172, July 2000. Cited on p. 84, 87, 90, 102

[1608] Senior, Andrew, “Facial Animation for Mobile GPUs,” in Wolfgang Engel, ed., ShaderX7, Charles River Media, pp. 561–570, 2009. Cited on p. 90

[841] Jones, James L., “Efficient Morph Target Animation Using OpenGL ES 3.0,” in Wolfgang Engel, ed., GPU Pro5 , CRC Press, pp. 289–295, 2014. Cited on p. 90

[1074] Lorach, Tristan, “DirectX 10 Blend Shapes: Breaking the Limits,” in Hubert Nguyen, ed., GPU Gems 3, Addison-Wesley, pp. 53–67, 2007. Cited on p. 90

[1971] Zink, Jason, Matt Pettineo, and Jack Hoxley, Practical Rendering & Computation with Direct3D 11, CRC Press, 2011. Cited on p. 47, 54, 90, 518, 519, 520, 568, 795, 813, 814, 914

[1872] Weronko, S., and S. Andreason, “Real-Time Transformations in The Order 1886,” in ACM SIGGRAPH 2015 Talks, ACM, article no. 8, Aug. 2015. Cited on p. 91

4.6 几何缓存回放 Geometry Cache Playback

在剪辑场景（cut scenes）中，可能希望使用极高质量的动画，例如，对于无法使用上述任何方法表示的运动。天真的方法是存储所有帧的所有顶点，从磁盘读取它们并更新网格。但是，对于短动画中使用的 30,000 个顶点的简单模型，这可能达到50 MB / s。Gneiting [545] 提出了几种将内存成本降低到大约10％的方法。

首先，使用量化（quantization）。例如，位置和纹理坐标使用每个坐标的 16 位整数存储。在执行压缩后无法恢复原始数据的意义上，这一步骤是有损的。为了进一步减少数据，进行了空间和时间预测，并对差异进行了编码。对于空间压缩，可以使用平行四边形预测 [800]。对于三角形带（triangle strip），下一个顶点的预测位置就是当前三角形在边缘周围的三角形平面中反射的三角形，从而形成平行四边形（parallelogram）。与新位置的差异接下来会被编码（encoded）。有了良好的预测，大多数值将接近零，这对于许多常用的压缩方案是十分理想的。与 MPEG 压缩类似，在时间维度上也会进行预测。也就是说，每 $n$ 帧执行一次空间压缩。在这两者之间，将在时间维度上进行预测，例如，如果某个特定顶点通过增量向量从帧 $n-1$ 移动到帧 $n$ ，则很可能以与帧 $n+1$ 相似的量移动。这些技术减少了存储量，从而足以使该系统用于实时流数据。

引用：

[545] Gneiting, A., “Real-Time Geometry Caches,” in ACM SIGGRAPH 2014 Talks, ACM, article no. 49, Aug. 2014. Cited on p. 92

[800] Isenberg, M., and P. Alliez, “Compressing Polygon Mesh Geometry with Parallelogram Prediction,” in Proceedings of the Conference on Visualization ’02, IEEE Computer Society, pp. 141–146, 2002. Cited on

4.7 投影 Projections

在实际渲染场景之前，必须将场景中的所有相关对象投影到某种平面或某种简单体积上。此后，执行裁剪和渲染（第 2.3 节）。

到目前为止，在本章中看到的变换不影响第四个坐标 $w$ 分量。也就是说，点和向量在转换后保留了其类型。另外，在 $4\times 4$ 矩阵中，最底行始终为 $(0\;0\;0\;1)$ 。透视投影矩阵（Perspective projection matrices）是这两个属性的例外：下一行包含矢量和点操作数，并且经常需要齐次化（homogenization）过程。也就是说， $w$ 通常不为 1，因此需要除以 $w$ 才能获得非齐次点。在本节中首先讨论的正交投影（Orthographic projection）是一种更简单的投影类型，也很常用。它不会影响 $w$ 分量。

在本部分中，我们假设观看者沿着相机的负 z 轴看，y 轴指向上方，x 轴指向右侧。换言之，这是一个右手坐标系。在某些文章和软件里（例如 DirectX）使用的是左手坐标系，在这些系统中，观看者沿着相机的正 z 轴看。这两种系统都是同等有效的，最后达到的效果是相同的。

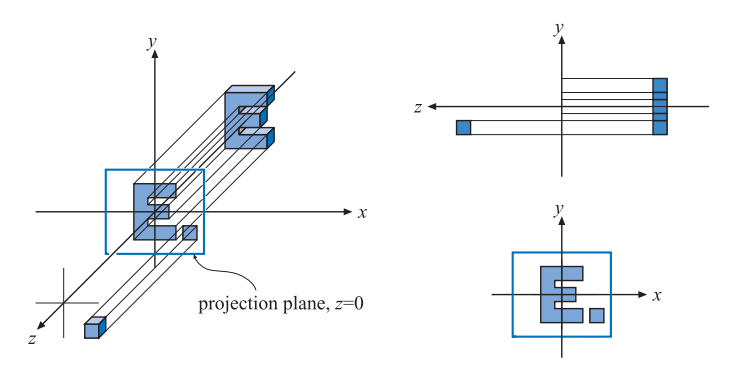
图4.17。由公式 4.62 生成的简单正投影的三种不同视图。当观看者沿着负 $z$ 轴看时，可以看到此投影，这意味着该投影仅跳过（或设置为零） $z$ 坐标，同时保持 $x$ 和 $y$ 坐标。请注意， $z=0$ 两侧的对象都投影到投影平面上。

4.7.1 正交投影 Orthographic Projection

正交投影的特征是平行线在投影之后保持平行。当使用正交投影观看场景时，无论与相机的距离如何，对象都保持相同的大小。矩阵 $\textbf{P}_{o}$ ，如下所示，是一个简单的正投影投影矩阵，它使一个点的 $x$ 和 $y$ 分量保持不变，而将 $z$ 分量设置为零，即正投影在平面 $z=0$ 上：

$\textbf{P}_{o}=\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(4.62)$

这种投影的效果如图 4.17 所示。显然， $\textbf{P}_{o}$ 是不可逆的，因为它的行列式 $\left | \textbf{P}_{o} \right |=0$ 。换句话说，变换从三维下降到二维，并且无法检索下降的维数。使用这种正交投影进行查看时存在的问题是，它将正 $z$ 点和负 $z$ 值的点都投影到投影平面上。通常将 $z$ 值（以及 $x$ 和 $y$ 值）限制为一定的间隔是很有用的，例如从 $n$ （近平面）到 $f$ （远平面）。(4) 这是下一个变换的目的。

用于执行正交投影的更常见矩阵由六元组 $(l,r,b,t,n,f)$ 表示，分别表示左侧（left），右侧（right），底部（bottom），顶部（top），近侧（near）和远侧（far）平面。该矩阵缩放并将由这些平面形成的与轴对齐的边界框（axis-aligned bounding box）（缩写为 AABB；请参见第22.2节中的定义）转换为以原点为中心的与轴对齐的立方体。AABB 的最小角为 $(l,b,n)$ ，最大角为
是 $(r,t,f)$ 。重要的是要意识到 $n>f$ ，因为我们正在向下看 $z$ 轴的负空间。我们的常识是，接近值应该比远端值低，因此，可以让用户按原样提供它们，然后在内部对它们取反（negate）。

在 OpenGL 中，与轴对齐的立方体的最小角为 $(-1,-1,-1)$ ，最大角为 $(1,1,1)$ 。在 DirectX 中，范围是 $(-1,-1,0)$ 到 $(1,1,1)$ 。此立方体称为规范视图体（canonical view volume），而该体积中的坐标称为规范化设备坐标（normalized device coordinates）。变换过程如图 4.18 所示。变换为标准视图体积的原因是在此处能够更有效地执行裁剪（clipping）。

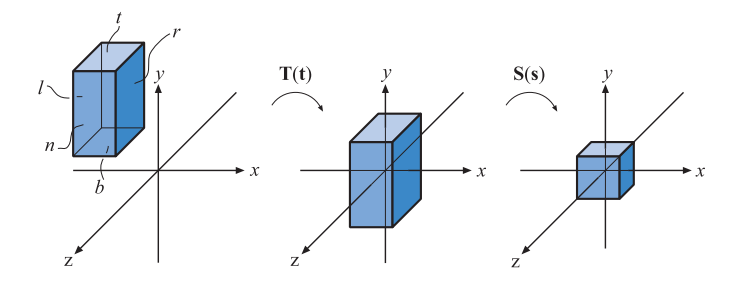
图4.18。变换规范视图体（canonical view volume）上的轴对齐框（axis-aligned box）。首先平移左侧的框，使其中心与原点重合。然后将其缩放以获取规范视图体的大小，如右侧所示。

变换为标准视图体（canonical view volume）后，将要渲染的几何图形的顶点裁剪（clipped）到该立方体上。最后，通过将剩余的单位正方形映射到屏幕来渲染不在立方体之外的几何图形。此正交变换如下所示：

$\large \\ \textbf{P}_{o}=\textbf{S}(\textbf{s})\textbf{T}(\textbf{t})=\begin{pmatrix} \frac{2}{r-l} & 0 & 0 & 0\\ 0 & \frac{2}{t-b} & 0 & 0\\ 0 & 0 & \frac{2}{f-n} & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 & -\frac{l+r}{2}\\ 0 & 1 & 0 & -\frac{t+b}{2}\\ 0 & 0 & 1 & -\frac{f+n}{2}\\ 0 & 0 & 0 & 1 \end{pmatrix}\;\;\;\;\;\;\;\;\;\;(4.63) \\ =\begin{pmatrix} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l}\\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b}\\ 0 & 0 & \frac{2}{f-n} & -\frac{f+n}{f-n}\\ 0 & 0 & 0 & 1 \end{pmatrix}.$

如该公式所示， $\textbf{P}_{o}$ 可以写为平移的串联 $\textbf{T}(\textbf{t})$ ，后面是缩放矩阵 $\textbf{S}(\textbf{s})$ ，其中 $\textbf{s}=(2/(r-l),2/(t-b),2/(f-n))$ 和 $\textbf{t}=(-(r+l)/2,-(t+b)/2,-(f+n)/2)$ 。该矩阵是可逆的，(5)，即 $\textbf{P}_{o}^{-1}=\textbf{T}(-\textbf{t})\textbf{S}((r-l)/2,(t-b)/2,(f-n)/2)$ 。

在计算机图形学中，投影后最常使用左手坐标系（left-hand coordinate system），即对于视口， $x$ 轴向右， $y$ 轴向上，而 $z$ 轴进入视口。因为按照我们定义 AABB 的方式，远值（far）小于近值（near），所以正交变换（orthographic transform）将始终包含镜像变换（mirroring transform）。要看到这一点，可以说原始的AABB尺寸与目标尺寸相同，即规范的视图体积。然后，AABB 的坐标是 $(l,\;b,\;n)$ 的 $(-1,-1,1)$ 和 $(r,\;t,\;f)$ 的 $(1,\;1,\;-1)$ 。将其应用于公式 4.63 可得出

$\textbf{P}_{o}=\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}, \;\;\;\;\;\;\;\;\;\;(4.64)$

这是一个镜像矩阵（mirroring matrix）。正是这种镜像将右手观察坐标系（从负 $z$ 轴向下看）转换为左手标准化设备坐标。

DirectX 将 $z$ 深度（ $z$ -depth）映射到 $[0,1]$ 范围，而不是OpenGL的 $[-1,1]$ 。这可以通过在正交矩阵之后应用简单的缩放和平移矩阵来实现，即

$\textbf{M}_{s t}=\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0.5 & 0.5\\ 0 & 0 & 0 & 1 \end{pmatrix}.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(4.65)$

因此，DirectX中使用的正交矩阵为

$\textbf{P}_{o[0,1]}=\begin{pmatrix} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l}\\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b}\\ 0 & 0 & \frac{1}{f-n} & -\frac{n}{f-n}\\ 0 & 0 & 0 & 1 \end{pmatrix}.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(4.66)$

由于 DirectX 使用行优先格式编写矩阵，因此通常以转置形式呈现。

作者注：

(4) 近平面也称为正平面（front plane）或 hither。远平面也称为背平面（back plane）或 yon。

(5) 当且仅当 $n \neq f,\;l \neq r$ 和 $t \neq b$ 时；否则，不存在逆（inverse）。

4.7.2 透视投影 Perspective Projection

透视投影比正交投影更复杂的变换是透视投影，它通常在大多数计算机图形应用程序中使用。在这里，平行线在投影后通常不平行；相反，它们可能会在极端情况下收敛到单个点。透视更紧密地匹配我们如何感知世界，即，更远的物体更小。

首先，我们将对投影到平面 $z=-d,\;d>0$ 上的透视投影矩阵进行推导。我们从世界空间中推导，以简化对世界视图转换的理解。此推导之后是例如 OpenGL [885] 中使用的更常规的矩阵。

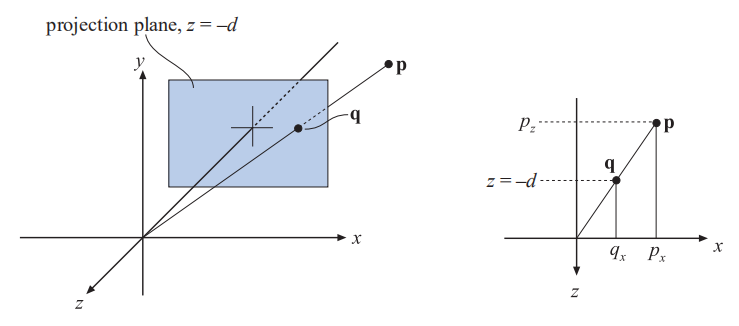
图4.19。用于导出透视投影矩阵（perspective projection matrix）的符号。将点 $\textbf{p}$ 投影到平面 $z=-d,\;d>0$ 上，得出投影点 $\textbf{q}$ 。投影是从摄影机位置的角度进行的，在本例中为原点。右侧的 $x$ 分量显示了推导中使用的相似三角形。

假设摄像机（视点）位于原点，并且我们要将一个点 $\textbf{p}$ 投影到平面 $z=-d,\;d>0$ ，从而产生一个新点 $q=(q_{x},q_{y},-d)$ 。图4.19 描绘了这种情况。从该图所示的相似三角形中，得出 $\textbf{q}$ 的 $x$ 分量的以下推导：

$\frac{q_{x}}{p_{x}}=\frac{-d}{p_{z}}\;\;\Leftrightarrow \;\;q_{x}=-d\frac{p_{x}}{p_{z}}.\;\;\;\;\;\;\;\;\;\;(4.67)$

$\textbf{q}$ 的其他分量的表达式为 $q_{y}=-dp_{y}/p_{z}$ （类似于 $q_{x}$ 获得）， $q_{z}=-d$ 。与上面的公式一起，它们给出了透视投影矩阵 $\textbf{P}_{p}$ ，如下所示：

$\textbf{P}_{p}=\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & -1/d & 0 \end{pmatrix}.\;\;\;\;\;\;\;\;\;\;(4.68)$

该矩阵可产生正确的透视投影，可通过以下方式确认

$\textbf{q}=\textbf{P}_{p}\textbf{p}=\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & -1/d & 0 \end{pmatrix} \begin{pmatrix} p_{x}\\ p_{y}\\ p_{z}\\ 1 \end{pmatrix} = \begin{pmatrix} p_{x}\\ p_{y}\\ p_{z}\\ -p_{z}/d \end{pmatrix} \Rightarrow \begin{pmatrix} -dp_{x}/p_{z}\\ -dp_{y}/p_{z}\\ -d\\ 1 \end{pmatrix}.\;\;\;\;\;\;\;\;\;\;(4.69)$

最后一步来自以下事实：整个矢量除以 $w$ 分量（在这种情况下为 $-p_{z}/d$ ），最后得到 1。由于我们要投影到该平面上，因此所得的 $z$ 值始终为 $-d$ 。

从直觉上讲，很容易理解为什么齐次坐标允许投影。齐次化过程的一种几何解释是将点 $(p_{x},\;p_{y},\;p_{z})$ 投影到平面 $w=1$ 上。

与正交变换（orthographic transformation）一样，还有一个透视变换（perspective transform），而不是实际投影到平面（不可逆）上，而是将视锥从视锥变换为前述的规范视像体。在这里，视锥视点假定从 $z=n$ 开始并在 $z=f$ 结束，且 $0>n>f$ 。 $z=n$ 处的矩形的最小角为 $(l,\;b,\;n)$ ，最大角为 $(r,\;t,\;n)$ 。如图 4.20 所示。

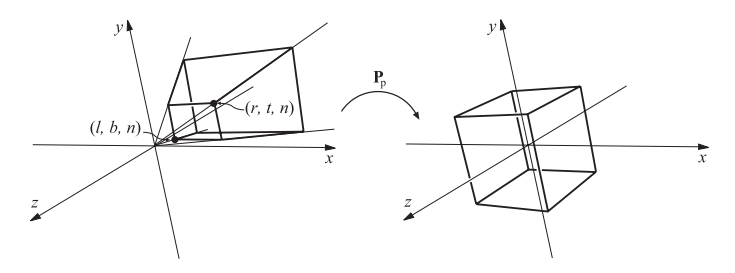
图4.20。矩阵 $\textbf{P}_{p}$ 将视锥体（view frustum）转换为单位立方体，称为标准视域（canonical view volume）。

参数 $(l,r,b,t,n,f)$ 确定摄像机的视锥（view frustum）。水平视野由视锥的左右平面（由 $l$ 和 $r$ 决定）之间的角度确定。以相同的方式，垂直视野由顶平面和底平面之间的角度（由 $t$ 和 $b$ 确定）确定。视野越大，相机“看得越多”。可以通过 $r\neq -l$ 或 $t\neq -b$ 来创建不对称视锥（Asymmetric frusta）。不对称视锥可用于立体观看（stereo viewing）和虚拟现实（virtual reality）（第 21.2.3 节）。

视野（the field of view）是提供场景感的重要因素。与计算机屏幕相比，眼睛本身具有物理视野。这种关系是

$\phi=2\textrm{arctan}(w/(2d)),\;\;\;\;\;\;\;\;\;\;(4.70)$

其中 $\phi$ 是视野， $w$ 是垂直于视线的物体的宽度， $d$ 是到物体的距离。例如，一个 25 英寸的显示器大约为 22 英寸宽。在 12 英寸远处，水平视野为 85 度；在 20 英寸处为 58 度；在 30 英寸，40 度可以使用相同的公式将摄像机镜头的尺寸转换为视野，例如，对于 35mm 摄像机的标准 50mm 镜头（镜框尺寸为 36mm）， $\phi=2\textrm{arctan}(36/(2.50))=39.6$ 度。

与物理设置相比，使用更窄的视野将减少透视效果，因为观看者将放大场景。设置较宽的视野将使对象看起来失真（例如使用广角相机镜头），尤其是在屏幕边缘附近，并且会放大附近对象的比例。然而，较宽的视野使观看者感觉到物体更大并且更令人印象深刻，并且具有向用户提供有关周围环境的更多信息的优点。

公式 4.71 给出了将视锥转化为单位立方体的透视变换矩阵：

$\large \textbf{P}_{p}=\begin{pmatrix} \frac{2n}{r-l} & 0 & -\frac{r+l}{r-l} & 0\\ 0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0\\ 0 & 0 & \frac{f+n}{f-n} & -\frac{2fn}{f-n}\\ 0 & 0 & 1 & 0 \end{pmatrix}.\;\;\;\;\;\;\;\;\;\;(4.71)$

将转换应用到一个点后，我们将得到另一个点 $\textbf{q}=(q_{x},q_{y},q_{z},q_{w})^{T}$ 。此时的 $w$ 分量 $q_{w}$ （通常）将为非零且不等于1。要获得投影点 $\textbf{p}$ ，我们需要除以 $q_{w}$ ，即

$\textbf{p}=(q_{x}/q_{w},\;q_{y}/q_{w},\;q_{z}/q_{w},1).\;\;\;\;\;\;\;\;\;\;(4.72)$

矩阵 $\textbf{P}_{p}$ 总是看到 $z=f$ 映射为 $+1$ ， $z=n$ 映射为 $-1$ 。

远平面以外的对象将被裁切，因此不会出现在场景中。另外，透视投影可以令远平面取到无穷远，这使公式 4.71 变为

$\large \textbf{P}_{p}=\begin{pmatrix} \frac{2n}{r-l} & 0 & -\frac{r+l}{r-l} & 0\\ 0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0\\ 0 & 0 & 1 & -2n\\ 0 & 0 & 1 & 0 \end{pmatrix}.\;\;\;\;\;\;\;\;\;\;(4.73)$

综上所述，应用透视变换（以任何形式） $\textbf{P}_{p}$ ，然后进行裁剪和齐次化（除以 $w$ ），从而得到标准化的设备坐标。

为了获得在 OpenGL 中使用的透视变换，出于与正交变换相同的原因，首先将其与 $\textbf{S}(1,1,-1,1)$ 相乘。这仅会使公式 4.71 第三栏中的值取反。在应用此镜像变换之后，将近距和远距值输入为正值，且 $0<n'<f'$ ，如传统上将其呈现给用户一样。但是，它们仍然代表沿世界负 $z$ 轴（即视线方向）的距离。出于参考目的，以下是 OpenGL 中的公式：

$\large \textbf{P}_{OpenGL}=\begin{pmatrix} \frac{2n'}{r-l} & 0 & \frac{r+l}{r-l} & 0\\ 0 & \frac{2n'}{t-b} & \frac{t+b}{t-b} & 0\\ 0 & 0 & -\frac{f'+n'}{f'-n'} & -\frac{2f'n'}{f'-n'}\\ 0 & 0 & -1 & 0 \end{pmatrix}.\;\;\;\;\;\;\;\;\;\;(4.74)$

一个更简单的设置是仅提供垂直视场 $\phi$ ，宽高比 $a=w/h$ （其中 $w\times h$ 是屏幕分辨率）， $n'$ 和 $f'$ 。这导致了

$\large \textbf{P}_{OpenGL}=\begin{pmatrix} c/a & 0 & 0 & 0\\ 0 & c & 0 & 0\\ 0 & 0 & -\frac{f'+n'}{f'-n'} & -\frac{2f'n'}{f'-n'}\\ 0 & 0 & -1 & 0 \end{pmatrix},\;\;\;\;\;\;\;\;\;\;(4.75)$

其中 $c=1.0/\textrm{tan}(\phi/2)$ 。该矩阵的作用与旧的 gluPerspective() 完全一样，后者是OpenGL Utility Library（GLU）的一部分。

某些API（例如 DirectX）将近平面映射到 $z=0$ （而不是 $z=-1$ ），而将远平面映射到 $z=1$ 。此外，DirectX 使用左手坐标系来定义其投影矩阵。这意味着 DirectX 沿 $z$ 轴正方向看，并以正数表示近和远值。这是 DirectX 公式：

$\large \textbf{P}_{p[0,1]}=\begin{pmatrix} \frac{2n'}{r-l} & 0 & -\frac{r+l}{r-l} & 0\\ 0 & \frac{2n'}{t-b} & -\frac{t+b}{t-b} & 0\\ 0 & 0 & \frac{f'}{f'-n'} & -\frac{f'n'}{f'-n'}\\ 0 & 0 & 1 & 0 \end{pmatrix}.\;\;\;\;\;\;\;\;\;\;(4.76)$

DirectX 在其文档中使用行优先形式，因此此矩阵通常以转置形式发送。

使用透视变换的一种效果是，计算出的深度值不会随输入 $\large \textbf{p}_{z}$ 值线性变化。使用公式 4.74 – 4.76 中的任何一个乘以点 $\large \textbf{p}$ 我们可以看到

$\large \textbf{v}=\textbf{P}_{\textbf{p}}=\begin{pmatrix} ...\\ ...\\ dp_{z}+e\\ \pm p_{z} \end{pmatrix},\;\;\;\;\;\;\;\;\;\;(4.77)$

其中省略了 $\large v_{x}$ 和 $\large v_{y}$ 的详细信息，并且常数 $\large d$ 和 $\large f$ 取决于所选矩阵。例如，如果我们使用公式 4.74，则 $d=-(f'+n')/(f'-n')$ ， $e=-2f'n'/(f'-n')$ 和 $v_{x} = -p_{z}$ 。为了获得归一化设备坐标（NDC）中的深度，我们需要除以 $w$ 分量，结果是

$\large z_{NDC}=\frac{dp_{z}+e}{-p_{z}}=d-\frac{e}{p_{z}},\;\;\;\;\;\;\;\;\;\;(4.78)$

其中 $\large z_{NDC}\;\epsilon \;[-1,+1]$ 用于 OpenGL 投影。可以看出，输出深度 $\large z_{NDC}$ 与输入深度 $\large p_{z}$ 成反比。

例如，如果 $n'=10$ 且 $f'=110$ （使用 OpenGL 术语），则当 $p_{z}$ 在负 $z$ 轴（即中点）下沿 60 个单位时，归一化设备坐标深度值为0.833，而不是 0。图 4.21 显示了改变近平面到原点的距离的影响。近平面和远平面的放置会影响 z 缓冲区的精度。第 23.7 节将进一步讨论这种效果。

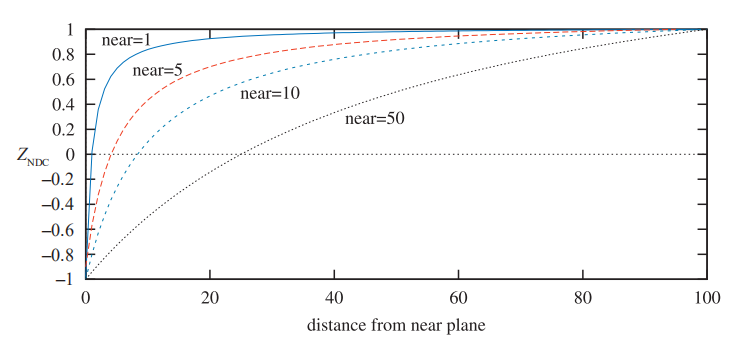
图4.21。改变近平面到原点的距离的影响。距离 $f'-n'$ 保持恒定为 100。随着近平面变得更靠近原点，更接近远平面的点将使用较小范围的归一化设备坐标（NDC）深度空间。这具有使 z 缓冲区在较大距离处的准确性降低的效果。

有几种增加深度精度的方法。一种常见的方法（我们称为反向 $z$ ， reversed $z$ ）是使用浮点深度或整数存储 1.0- $z_{NDC}$ [978]。比较如图 4.22 所示。Reed [1472]通过仿真显示，使用具有反向 z 的浮点缓冲区可提供最佳精度，这也是整数深度缓冲区（每个深度通常具有24位）的首选方法。对于标准映射（即非反向 $z$ ），如 Upchurch 和 Des brun [1803]所建议的，在变换中分离投影矩阵可降低错误率。例如，在 $\textbf{T}=\textbf{PM}$ 的情况下，使用 $\textbf{P}(\textbf{Mp})$ 比使用 $\textbf{Tp}$ 更好。同样，在 [0.5，1.0] 范围内，fp32 和 int24 的精度非常相似，因为 fp32 具有 23 位的尾数。使 $z_{NDC}$ 与 $1/p_{z}$ 成比例的原因是，它使硬件更简单，并且深度压缩更成功，这将在 23.7 节中详细讨论。

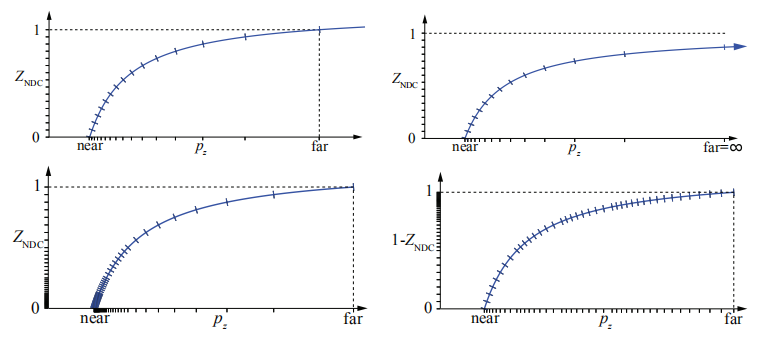
图4.22。使用 DirectX 变换设置深度缓冲区的不同方法，即 $z_{NDC}\;\epsilon \;[0,+1]$ 。左上方：标准整数深度缓冲区，此处显示为4位精度（因此 y 轴上有 16 个标记）。右上角：远平面设置为 ∞，两个轴上的微小偏移表明这样做不会损失太多精度。左下：具有3个指数位和 3 个尾数位用于浮点深度。注意，分布在y轴上是非线性的，这使得在x轴上的分布更糟。右下角：反转的浮点深度，即 $1-z_{NDC}$ ，结果分布更好。（插图由内森·里德（Nathan Reed）提供。）

Lloyd [1063]提出使用深度值的对数来提高阴影贴图的精度。Lauritzen 等。[991]使用前一帧的 $z$ 缓冲区（ $z$ -buffer）来确定最大近平面和最小远平面。对于屏幕空间深度，Kemen [881]建议对每个顶点使用以下重新映射：

$\\ z=w(\textrm{log}_{2}(\textrm{max}(10^{-6},1+w))f_{c}-1),\;\;\;\;\;[\textrm{OpenGL}]\;\;\;\;\;\;\;\;\;\;(4.79) \\ z=w\textrm{log}_{2}(\textrm{max}(10^{-6},1+w))f_{c}/2,\;\;\;\;\;[\textrm{DirectX}]$

其中w是投影矩阵之后的顶点的 $w$ 值，而 $z$ 是顶点着色器的输出 $z$ 。常数 $f_{c}$ 为 $f_{c}=2/\textrm{log}_{2}(f+1)$ ，其中 $f$ 为远平面。当仅在顶点着色器中应用此变换时，深度仍将由 GPU 在顶点的非线性变换深度之间在三角形上线性插值（公式 4.79）。由于对数是单调函数，因此只要分段线性插值与精确的非线性变换深度值之间的差异较小，遮挡剔除硬件和深度压缩技术仍将起作用。在大多数情况下，具有足够的几何细分的情况是正确的。但是，也可以对每个片段应用转换。这是通过输出每个顶点的值 $e=1+w$ 来完成的，然后由 GPU 在三角形上进行插值。然后，像素着色器将片段深度修改为 $\textrm{log}^{2}(e_{i})f_{c}/2$ ，其中 $e_{i}$ 是 $e$ 的内插值。当 GPU 中没有浮点深度并且使用深度较大的距离进行渲染时，此方法是不错的选择。

Cozzi [1605]建议使用多视锥（multiple frusta），这可以提高准确度以有效地达到任何期望的比率。视锥在深度方向上分为几个不重叠的较小的子视锥，它们的联合恰好是视锥。子视锥表以从后到前的顺序渲染。首先，清除颜色和深度缓冲区，并将所有要渲染的对象分类到它们重叠的每个子视锥中。对于每个子视锥，设置其投影矩阵，清除深度缓冲区，然后渲染与子视锥重叠的对象。

引用：

[885] Kessenich, John, Graham Sellers, and Dave Shreiner, OpenGL Programming Guide: The Of-ficial Guide to Learning OpenGL, Version 4.5 with SPIR-V, Ninth Edition, Addison-Wesley, 2016. Cited on p. 27, 39, 41, 55, 96, 173, 174

[978] Lapidous, Eugene, and Guofang Jiao, “Optimal Depth Buffer for Low-Cost Graphics Hardware,”in Proceedings of the ACM SIGGRAPH/EUROGRAPHICS Workshop on Graphics Hardware, ACM, pp. 67–73, Aug. 1999. Cited on p. 100

[1472] Reed, Nathan, “Depth Precision Visualized,” Nathan Reed blog, July 3, 2015. Cited on p. 100, 1014

[1803] Upchurch, Paul, and Mathieu Desbrun, “Tightening the Precision of Perspective Rendering,”journal of graphics tools, vol. 16, no. 1, pp. 40–56, 2012. Cited on p. 101

[1063] Lloyd, Brandon, Logarithmic Perspective Shadow Maps, PhD thesis, Dept. of Computer Science, University of North Carolina at Chapel Hill, Aug. 2007. Cited on p. 101, 241, 242

[991] Lauritzen, Andrew, Marco Salvi, and Aaron Lefohn, “Sample Distribution Shadow Maps,” in Symposium on Interactive 3D Graphics and Games, ACM, pp. 97–102, Feb. 2011. Cited on p. 54, 101, 244, 245

[881] Kemen, B., “Logarithmic Depth Buffer Optimizations & Fixes,” Outerra blog, July 18, 2013. Cited on p. 101

[1605] Sellers, Graham, Patrick Cozzi, Kevin Ring, Emil Persson, Joel da Vahl, and J. M. P. van Waveren, SIGGRAPH Rendering Massive Virtual Worlds course, July 2013. Cited on p. 102, 868, 874, 875, 876, 879

进一步阅读和资源

沉浸式的线性代数网站 [1718]提供了一本有关该主题基础知识的互动书籍，通过鼓励您操纵这些数字来帮助建立直觉。来自 realtimerendering.com 的其他交互式学习工具和变换代码库也已链接至此。

Farin和Hansford的《The Geometry Toolbox》 [461]是一本可以毫不费力地增强人们对矩阵直觉的书籍。另一本有用的著作是Lengyel 的《Mathematics for 3D Game Programming and Computer Graphics》 [1025]。若想从不同的角度来看，那么也有许多计算机图形学的著作，例如 Hearn 和 Baker [689]，Marschner 和 Shirley [1129] 和 Hughes 等人的著作 [785] 介绍了矩阵基础知识。Ochiai 等人的课程 [1310]介绍了矩阵基础以及矩阵的指数和对数，以及用于计算机图形学的知识。Graphics Gems 系列 [72，540，695，902，1344]提出了各种与变换相关的算法，并且在线提供了许多此类算法的代码。Golub 和 Van Loan 的 Matrix Computations [556]通常是认真研究矩阵技术的起点。可以在 Lewis 等人的 SIGGRAPH 论文 [1037]中阅读有关骨骼子空间（skeleton-subspace）变形/顶点混合（deformation/vertex blending）和形状插值（shape interpolation）的更多信息。

哈特等。[674]和汉森 [663]提供了四元数的可视化。Plet inckx [1421]和 Schlag [1566]提出了在一组四元数之间平滑内插的不同方法。Vlachos 和 Isidoro [1820]推导了四元数的C2插值公式。另外，与四元数插值有关的是沿曲线计算一致坐标系的问题，是由Dougan [374]处理的。

Alexa [28] 和 Lazarus and Verroust [1000]对许多不同的变形技术进行了调查。Parent’s book [1354]是有关计算机动画技术的绝佳来源。

引用：

[1718] Str¨om, J., K. ˚Astr¨om, and T. Akenine-M¨oller, “Immersive Linear Algebra,” http://immersivemath.com, 2015. Cited on p. 102, 1047

[461] Farin, Gerald E., and Dianne Hansford, Practical Linear Algebra: A Geometry Toolbox, A K Peters, Ltd., 2004. Cited on p. 102, 991

[1025] Lengyel, Eric, Mathematics for 3D Game Programming and Computer Graphics, Third Edition, Charles River Media, 2011. Cited on p. 102, 209, 210

[689] Hearn, Donald, and M. Pauline Baker, Computer Graphics with OpenGL, Fourth Edition, Prentice-Hall, Inc., 2010. Cited on p. 102

[1129] Marschner, Steve, and Peter Shirley, Fundamentals of Computer Graphics, Fourth Edition, CRC Press, 2015. Cited on p. 102

[785] Hughes, John F., Andries van Dam, Morgan McGuire, David F. Sklar, James D. Foley, Steven K. Feiner, and Kurt Akeley, Computer Graphics: Principles and Practice, Third Edition, Addison-Wesley, 2013. Cited on p. 102, 278

[1310] Ochiai, H., K. Anjyo, and A. Kimura, SIGGRAPH An Elementary Introduction to Matrix Exponential for CG course, July 2016. Cited on p. 102

[72] Arvo, James, ed., Graphics Gems II, Academic Press, 1991. Cited on p. 102, 991

[540] Glassner, Andrew S., ed., Graphics Gems, Academic Press, 1990. Cited on p. 102, 991

[695] Heckbert, Paul S., ed., Graphics Gems IV, Academic Press, 1994. Cited on p. 102, 991

[902] Kirk, David, ed., Graphics Gems III, Academic Press, 1992. Cited on p. 102, 991

[1344] Paeth, Alan W., ed., Graphics Gems V, Academic Press, 1995. Cited on p. 102, 991

[556] Golub, Gene, and Charles Van Loan, Matrix Computations, Fourth Edition, Johns Hopkins University Press, 2012. Cited on p. 102

[674] Hart, John C., George K. Francis, and Louis H. Kauffman, “Visualizing Quaternion Rotation,”ACM Transactions on Graphics, vol. 13, no. 3, pp. 256–276, 1994. Cited on p. 102

[663] Hanson, Andrew J., Visualizing Quaternions, Morgan Kaufmann, 2006. Cited on p. 102

[1421] Pletinckx, Daniel, “Quaternion Calculus as a Basic Tool in Computer Graphics,” The Visual Computer, vol. 5, no. 1, pp. 2–13, 1989. Cited on p. 102

[1566] Schlag, John, “Using Geometric Constructions to Interpolate Orientations with Quaternions,” in James Arvo, ed., Graphics Gems II, Academic Press, pp. 377–380, 1991. Cited on p. 102

[1820] Vlachos, Alex, and John Isidoro, “Smooth C2 Quaternion-Based Flythrough Paths,” in Mark DeLoura, ed., Game Programming Gems 2, Charles River Media, pp. 220–227, 2001. Cited on p. 102

[374] Dougan, Carl, “The Parallel Transport Frame,” in Mark DeLoura, ed., Game Programming Gems 2, Charles River Media, pp. 215–219, 2001. Cited on p. 102

[28] Alexa, Marc, “Recent Advances in Mesh Morphing,” Computer Graphics Forum, vol. 21, no. 2, pp. 173–197, 2002. Cited on p. 87, 88, 102

[1000] Lazarus, F., and A. Verroust, “Three-Dimensional Metamorphosis: A Survey,” The Visual Computer, vol. 14, no. 8, pp. 373–389, 1998. Cited on p. 87, 102

[1354] Parent, R., Computer Animation: Algorithms & Techniques, Third Edition, Morgan Kaufmann, 2012. Cited on p. 102