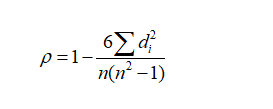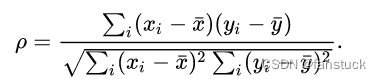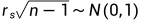在统计数据中,斯皮尔曼的等级相关系数或斯皮尔曼的rho,以查尔斯斯皮尔曼命名并经常用希腊字母表示或
,是秩相关的非参数度量(两个变量的排名之间的统计依赖性)。它评估了使用单调函数描述两个变量之间关系的程度。
两个变量之间的Spearman相关性等于这两个变量的秩值之间的Pearson相关性 ; 当Pearson的相关性评估线性关系时,Spearman的相关性评估单调关系(无论是线性的还是非线性关系)。如果没有重复的数据值,当每个变量是另一个的完美单调函数时,发生+1或-1的完美斯皮尔曼相关。
直观地,当两个变量之间的观察具有相似(或相关的1)等级(即变量内的观察的相对位置标签:第一,第二,第三等)时,两个变量之间的Spearman相关性将是高的。当观察结果与两个变量之间具有不相似(或完全相反的相关性)时,变量和低值。
Spearman系数适用于连续和离散序数变量。Spearman's 和肯德尔的
可以表述为更一般的相关系数的特殊情况。
定义和计算
Spearman相关系数定义为排序变量之间的Pearson相关系数。
对于大小的样品n,所述n 原始分数,
转换为排名
,
,和
计算自:
表示通常的Pearson相关系数,但应用于秩变量。
是秩变量的协方差。
和
是秩变量的标准偏差。
只有当所有n个等级都是不同的整数时,才能使用流行的公式计算
,是每个观察的两个等级之间的差异。
- n是观察的数量
相同的值通常是,每个分配的小数等级等于它们在值的升序中的位置的平均值,这相当于对所有可能的排列进行平均。
如果数据集中存在联系,则上面的简化公式会产生不正确的结果:只有在两个变量中,所有等级都是不同的,那么 
这个在数据集被截断的情况下也不应使用]方法; 也就是说,当前X个记录(无论是通过改变前等级还是改变后等级,或两者)都需要Spearman相关系数时,用户应使用上面给出的Pearson相关系数公式。
系数(σ)的标准误差由Pearson于1907年和Gosset于1920年确定
相关数量
还有一些其他数值测量可以量化观察对之间统计依赖的程度。其中最常见的是Pearson积矩相关系数,它是与Spearman等级相似的相关方法,用于衡量原始数字之间而不是等级之间的“线性”关系。
Spearman 等级相关的另一个名称是“等级相关”;观察的“等级”被“等级”取代。在连续分布中,按照惯例,观察等级总是比等级小一半,因此在这种情况下等级和等级相关性是相同的。更一般地,观察的“等级”与小于给定值的总体分数的估计成比例,半观察调整在观察值处。因此,这对应于绑定等级的一种可能的处理。虽然不寻常,但“等级相关”一词仍在使用中。
解释
Spearman相关的符号表示X(自变量)和Y(因变量)之间的关联方向。如果 X在X增加时趋于增加,则Spearman相关系数为正。如果X在X增加时趋于减小,则Spearman相关系数为负。Spearman相关系数为零表示当X增加时Y没有增加或减少的趋势。随着X和Y变得更接近彼此的完美单调函数,Spearman相关性的幅度增加。什么时候X和Y完全单调相关,Spearman相关系数变为1.完美的单调增加关系意味着对于任何两对数据值X i,Y i和X j,Y j,X i - X j和Y i - Y j总是有相同的符号。完美的单调递减关系意味着这些差异总是具有相反的符号。
Spearman相关系数通常被描述为“非参数”。这可以有两个含义。首先,当X和Y通过任何单调函数相关时,产生完美的Spearman相关性。将此与Pearson相关性进行对比,Pearson相关性仅在X和Y通过线性函数相关时给出完美值。其他感测,其中所述Spearman相关是,在不需要知识来获得其准确的采样分布(非参数即,知道参数)的接头的概率分布的X和Y。
示例
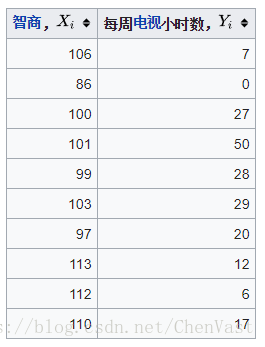
在此示例中,下表中的原始数据用于计算人的智商与每周在电视机前花费的小时数之间的相关性。
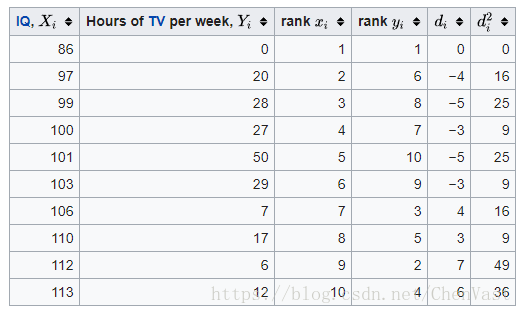
首先,评估
- 按第一列排序数据(
)。创建一个新列{\ displaystyle x_ {i}}
并为其分配排名值1,2,3,... n。
- 接下来,按第二列对数据进行排序(
)。创建第四列
并且类似地为其分配排名值1,2,3,... n。
- 创建第五列
保持两个等级列之间的差异(
和
)。
- 创建一个最终列
保持列的值
平方。
同 


其评估为ρ = -29 / 165 = -0.175757575 ... ,P值 = 0.627188(使用t分布)。
这个低值表明智商和看电视的时间之间的相关性非常低,尽管负值表明看电视的时间越长智商越低。如果是原始值的关系,则不应使用此公式; 相反,应该在等级上计算Pearson相关系数(其中关系被赋予等级,如上所述)。

提供的数据图表。可以看出,可能存在负相关,但这种关系似乎不是确定的。
基于Spearman的rho的对应分析
经典对应分析是一种统计方法,可以对两个名义变量的每个值进行分数。通过这种方式,它们之间的Pearson 相关系数最大化。
这种方法有一种称为等级对应分析的方法,可以最大化Spearman的rho或Kendall的tau。
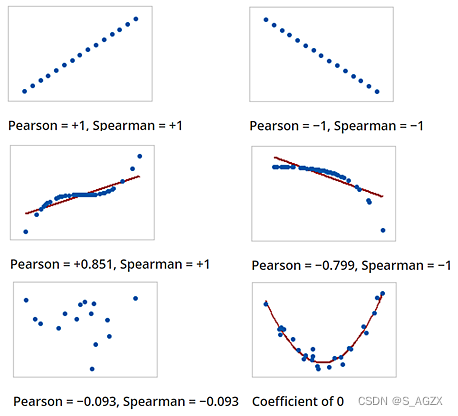
图示

当比较的两个变量是单调相关的,即使它们的关系不是线性的,Spearman相关性为1。这意味着x值大于给定数据点的所有数据点也将具有更大的y值。相比之下,这并没有给出完美的Pearson相关性。

当数据大致呈椭圆分布且没有明显的异常值时,Spearman相关和Pearson相关给出相似的值。

Spearman相关性不如Pearson相关性对两个样本尾部的强异常值敏感。那是因为斯皮尔曼的rho将异常值限制在其等级值。

正斯皮尔曼相关系数对应于X和Y之间增加的单调趋势。

负Spearman相关系数对应于X和Y之间的单调趋势减小。
参考文献:https://en.wikipedia.org/wiki/Spearman%27s_rank_correlation_coefficient