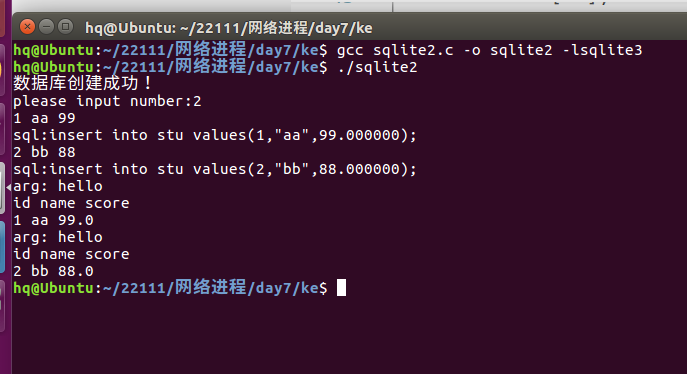
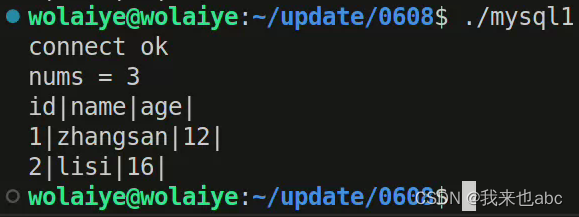
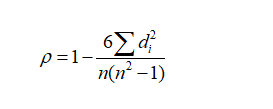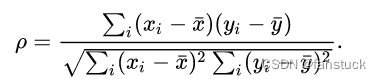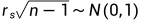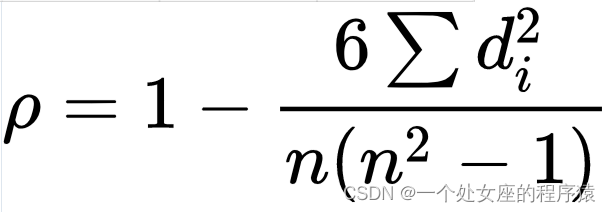1.1总体皮尔逊（person）相关系数：

在概率论与数理统计中我们学到，若两组数据X{x1，x2…xn}与Y{y1，y2…yn}为总体数据，则总体协方差为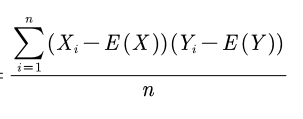
它表示两个变量的总体误差，若XY相对于各自均值同向变化，为正值，反之为负值。其数值与数据本身量纲有关。
则总体皮尔逊相关系数为上面的协方差除以X与Y的标准差。即：

可以看成是剔除了两个变量量纲影响，即将X和Y标准化后的协方差。

1.2 样本皮尔逊相关系数：
与上面类似，XY是两组样本数据。样本的协方差与标准差分母改成n-1即可：


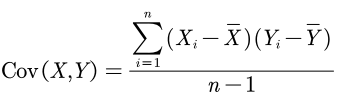
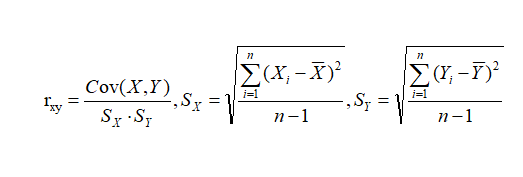
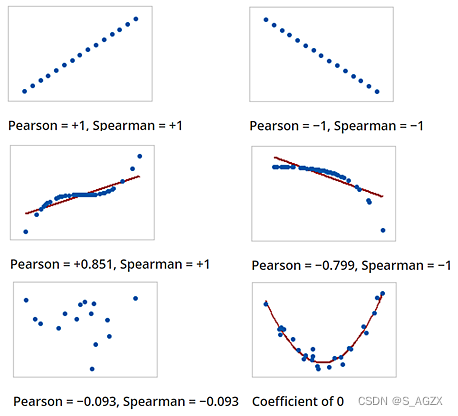
通过绘制散点图，我们可以清楚的看出x与y的相关性：

注：
1.我们只能通过这种方法衡量X与Y线性相关的程度，若两组本身不是线性关系，那么结果并不具有说服力。一定要先判断两变量是否是线性关系！
2.野值对结果存在影响。
3.计算得出的相关性结果是大是小需要根据不同的背景来解释。

1.3 进行假设检验来判断其显著性：
原假设H0：相关系数r=0 ；H1：r≠0。对于这里的皮尔逊相关系数来说，满足一定条件时，我们可以认为它是服从自由度为n-2的t分布。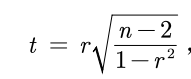
在后面的MATLAB代码中，方便起见，我们用到了p值判别法，计算相关系数矩阵的元素对应的p值（当p<0.01时，在99%的置信水平上拒绝H0，其他同理）

---

例题：

我们将数据导入spss，利用描述功能，我们可以得出一些基本信息

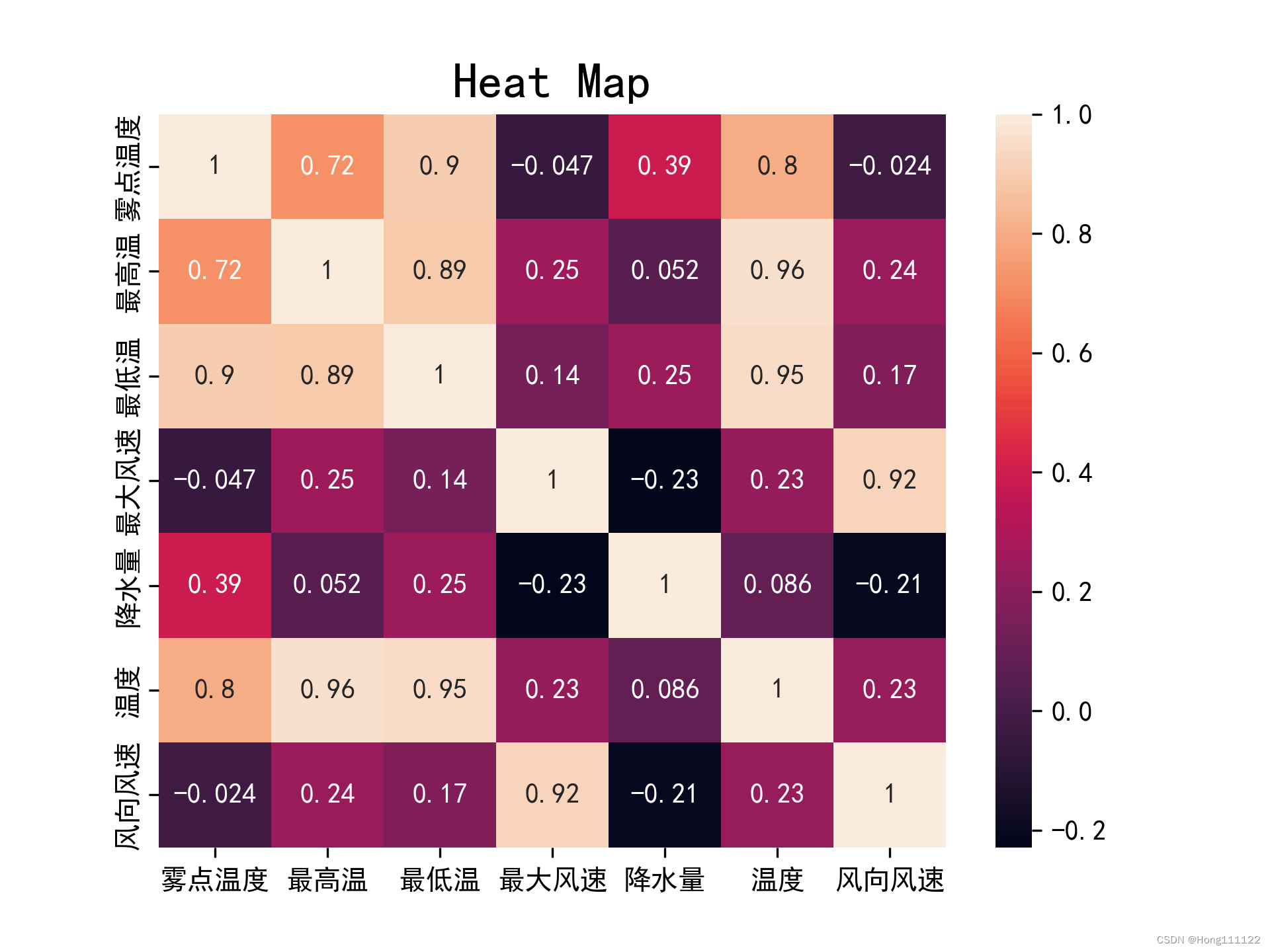
我们接下来看一下两两变量的线性关系，利用spss的矩阵散点图做出：

我们可以看出，两两的线性关系并不太好，但是为了演示后面的过程，我们假设这里是满足线性的。
接下来用MATLAB来进行后续的操作

[R,P] = corrcoef(PE_Test) %PE_Test为体侧的数据，corrcoef函数是求相关系数的函数，R为相关系数，P为p值

运行结果：

---

我们如何判断数据是否是正态分布？
2.1雅克‐贝拉检验(Jarque‐Bera test)，适用于大样本（n>30）
在这种方法中，主要是通过比较偏度与峰度来判断

H0为变量服从正态分布；H1为不服从，一般取α=0.05（95%置信区间）

MATLAB代码：

% 以下两行为检验第一列数据是否为正态分布
%[h,p] = jbtest(PE_Test(:,1),0.05) 当p<0.05时，在95%的置信水平上拒绝H0
%[h,p] = jbtest(PE_Test(:,1),0.01) 当p<0.01时，在99%的置信水平上拒绝H0，则h=1，反之h=0% 用循环检验所有列的数据
n_c = size(PE_Test,2);  % number of column 数据的列数
H = zeros(1,6);  %预分配,初始化
P = zeros(1,6);
for i = 1:n_c[h,p] = jbtest(PE_Test(:,i),0.05);H(i)=h;P(i)=p;
end
disp(H) %运行结果为H全是1，不服从正态分布
disp(P)

2.2Shapiro‐wilk夏皮洛‐威尔克检验，适用于小样本（3<=n<=50）:
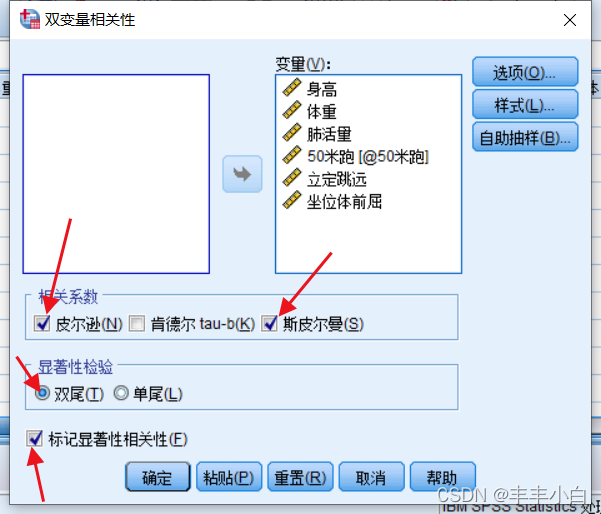
与上面类似，H0为服从正态分布，H1为不服从。α默认0.05，为了满足条件，我选取的前三十组数据，并使用spss操作：


可以看到，身高，立定跳远与坐位体前屈大于0.05，即无法拒绝原假设，是正态分布的。

身高的qq图大体上表现为线性，但要注意，这里的n并不大，可能qq图的说服力并不强。

2.3 qq图：
Q‐Q图（Q代表分位数Quantile）是一种通过比较两个概率分布的分位数对这两个概率分布进行比较的概率图方法。首先选定分位数的对应概率区间集合，在此概率区间上，点(x,y)对应于第一个分布的一个分位数x和第二个分布在和x相同概率区间上相同的分位数。
这里，我们选择正态分布和要检验的随机变量，并对其做出QQ图，可想而知，如果要检验的随机变量是正态分布，那么QQ图就是一条直线。要利用Q‐Q图鉴别样本数据是否近似于正态分布,只需看Q‐Q图上的点是否近似地在一条直线附近。（数据量最好非常大）

---

在第一部分的皮尔逊相关系数的内容中，我们可以看出他需要满足许多条件：
(1)、两个变量之间是线性关系，都是连续数据。
(2)、两个变量的总体是正态分布，或接近正态的单峰分布。
(3)、两个变量的观测值是成对的，每对观测值之间相互独立。（引用自Leaveager的博客https://blog.csdn.net/qq_30142403/article/details/82350628）
但如果有一条不满足呢？接下来，我们将介绍第三部分，斯皮尔曼（spearman）相关系数！

3.1斯皮尔曼相关系数的定义：
斯皮尔曼相关性系数，通常也叫斯皮尔曼秩相关系数。“秩”，可以理解成就是一种顺序或者排序，那么它就是根据原始数据的排序位置进行求解，这种表征形式就没有了求皮尔森相关性系数时那些限制。它的适用范围更广，但面对特定问题时，可能不够准确，如两个变量满足上面的（1）（2）（3），则优先考虑皮尔逊相关系数。

3.2 数学表达：
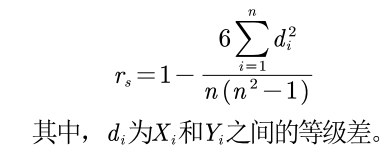rs位于-1到1.
举个例子

代入公式可计算出rs=0.875。

3.3 MATLAB代码：

%% MATLAB求解斯皮尔曼
X = [3 8 4 7 2]' % 一定要用列向量！
Y = [5 10 9 10 6]'
coeff = corr(X , Y , 'type' , 'Spearman')

3.4 又到了爷最爱的假设检验环节
当样本较小时，我们可以直接查表。但样本大的话，遵循下面的公式

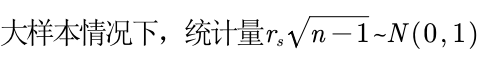
H0：rs=0；H1：rs不等于0。

当然，我们可以不用考虑上面的情况，直接用代码来解决：

% 直接给出相关系数R和p值,和上面皮尔逊差不多
%[R,P]=corr(PE_Test, 'type' , 'Spearman')

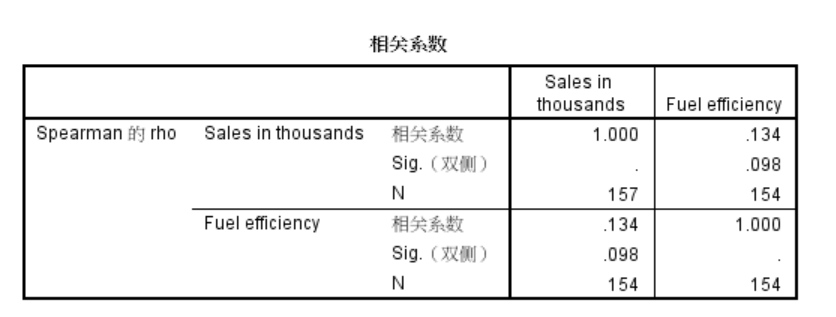
结果和皮尔逊的确实不太一样。