定义
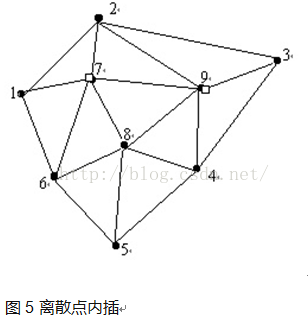
\qquad 给定开集 Ω ⊆ R N \Omega\subseteq\mathbb{R}^{N} Ω⊆RN，如果当 i ≠ j i\ne j i̸=j且 ∪ i = 1 k V i ˉ = Ω ˉ \cup_{i=1}^{k}\bar{V_{i}}=\bar{\Omega} ∪i=1kViˉ=Ωˉ时 V i ∩ V j = ∅ V_{i}\cap V_{j}=\emptyset Vi∩Vj=∅则集合 { V i } i = 1 k \{V_{i}\}^{k}_{i=1} {Vi}i=1k称为开集 Ω \Omega Ω的 t e s s e l l a t i o n tessellation tessellation。使用 ∣ ⋅ ∣ |\cdot| ∣⋅∣定义欧几里得范数。给定属于 Ω ˉ 的 \bar{\Omega}的 Ωˉ的点集 { z i } i = 1 k \{z_{i}\}^{k}_{i=1} {zi}i=1k，对应点 z i z_{i} zi的 V o r o n o i Voronoi Voronoi范围 V i ^ \hat{V_{i}} Vi^：
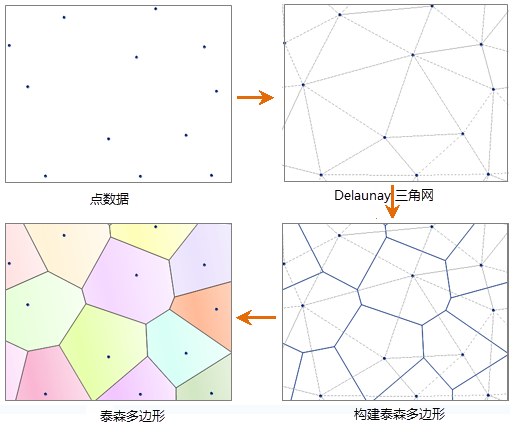
V i ^ = { x ∈ Ω ∣ ∣ x − z i ∣ < ∣ x − z j ∣ f o r j = 1 , . . . , k , j ≠ i } ( 1 ) \hat{V_{i}}=\{x\in\Omega||x-z_{i}|<|x-z_{j}|\ for\ j=1,...,k,j\ne i\}\qquad(1) Vi^={x∈Ω∣∣x−zi∣<∣x−zj∣ for j=1,...,k,j̸=i}(1) \qquad 点集 { z i } i = 1 k \{z_{i}\}^{k}_{i=1} {zi}i=1k称为生成点。集合 { V i ^ } i = 1 k \{\hat{V_{i}}\}_{i=1}^{k} {Vi^}i=1k称为开集 Ω \Omega Ω的 V o r o n o i t e s s e l l a t i o n Voronoi\ tessellation Voronoi tessellation或者 V o r o n o i d i a g r a m Voronoi\ diagram Voronoi diagram，每个 { V i ^ } \{\hat{V_{i}}\} {Vi^}区域都是点 z i z_{i} zi对应的 V o r o n o i Voronoi Voronoi区域。 V o r o n o i Voronoi Voronoi区域是多面体， t e s s e l l a t i o n tessellation tessellation有着广泛地应用。
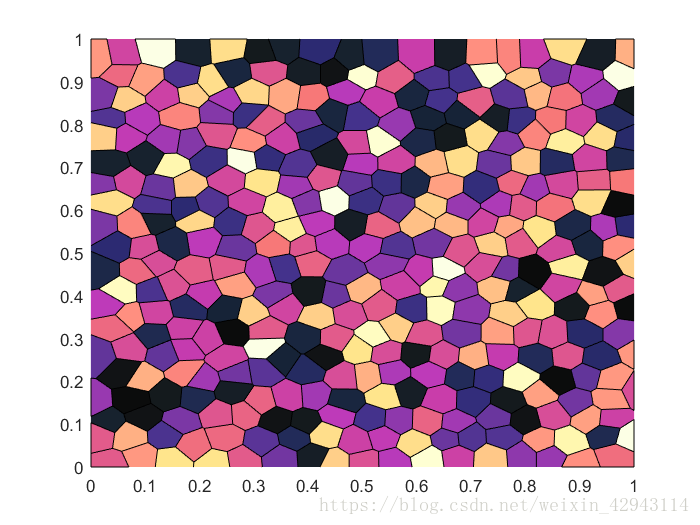
\qquad 左边图为由10个随机点生成(是由一组由连接两邻点直线的垂直平分线组成的连续多边形组成)的泰森多边形区域，密度函数为常数。点为泰森多边形生成点，圆圈对应为每个泰森多边形的形心，生成点和形心不在同一位置。右边为中心泰森多边形镶嵌法( centroidal Voronoi tessellation),点代表生成点和形心，即两点在相同位置。
\qquad 给定区域 V ⊆ R N V\subseteq\mathbb{R}^{N} V⊆RN及其密度函数 ρ \rho ρ，则V的重心 z ∗ z^{*} z∗：
z ∗ = ∫ V y ρ ( y ) d y ∫ V ρ ( y ) d y ( 2 ) z^{*}=\frac{\int_{V} y\rho(y)dy}{\int_{V} \rho(y)dy}\qquad(2) z∗=∫Vρ(y)dy∫Vyρ(y)dy(2) \qquad 更一般化的定义区域中心 z ∗ z^{*} z∗的方法为：
∫ V ρ ( y ) d ( z ∗ , y ) d y = i n f z ∈ V ∗ ∫ V ρ ( y ) d ( z , y ) d y ( 3 ) \int_{V}\rho(y)d(z^{*},y)dy=\mathop{inf}\limits_{z\in V^{*}}\int_{V}\rho(y)d(z,y)dy\qquad(3) ∫Vρ(y)d(z∗,y)dy=z∈V∗inf∫Vρ(y)d(z,y)dy(3) \qquad 给定 k k k个点 z i , i = 1 , . . . , k z_{i},\ i=1,...,k zi, i=1,...,k后即可获得泰森多边形区域 V i ^ , i = 1 , . . . , k \hat{V_{i}},\ i=1,...,k Vi^, i=1,...,k,然后就能获得对应的质心点 z i ∗ z_{i}^{*} zi∗，而在应用中所期望的为:
z i = z i ∗ , i = 1 , . . . k , ( 4 ) z_{i}=z_{i}^{*},\qquad i=1,...k,\qquad(4) zi=zi∗,i=1,...k,(4) \qquad 此时，称 t e s s e l l a t i o n tessellation tessellation为 c e n t r o i d a l V o r o n o i t e s s e l l a t i o n centroidal\ Voronoi\ tessellation centroidal Voronoi tessellation,求解该问题可以转化为：
给 定 ： 给定： 给定：
区 域 Ω ⊆ R N \qquad区域\Omega\subseteq\mathbb{R}^{N} 区域Ω⊆RN
正 整 数 k 、 密 度 函 数 ρ 、 在 Ω 中 定 义 变 量 y \qquad 正整数k、密度函数\rho、在\Omega中定义变量y 正整数k、密度函数ρ、在Ω中定义变量y
求 解 ： 求解： 求解：
k 个 生 成 点 z i ， 其 中 z i ∈ Ω \qquad k个生成点z_{i}，其中z_{i}\in\Omega k个生成点zi，其中zi∈Ω
k 个 在 Ω 中 的 泰 森 多 边 形 区 域 \qquad k个在\Omega中的泰森多边形区域 k个在Ω中的泰森多边形区域
定位最优化问题
\qquad 泰森多边形不仅应用在空间分析表示还可以应用在位置最优化方面。下文中将主要介绍定位最优化问题。
\qquad 一般性的最优化问题为：
m i n x 1 , . . . x n F ( x 1 , . . . x n ) ( 5 ) \mathop{min}\limits_{x_{1},...x_{n}}F(x_{1},...x_{n})\qquad(5) x1,...xnminF(x1,...xn)(5) s . t . s.t. s.t. g i ( x 1 , . . . , x n ) ≤ 0 , i = 1 , . . . , m 1 g i ( x 1 , . . . , x n ) = 0 , i = m 1 + 1 , . . . , m 1 + m 2 ( 6 ) g_{i}(x_{1},...,x_{n})\leq0 ,\ i=1,...,m_{1}\\ g_{i}(x_{1},...,x_{n})=0,\ i=m_{1}+1,...,m_{1}+m_{2}\qquad(6) gi(x1,...,xn)≤0, i=1,...,m1gi(x1,...,xn)=0, i=m1+1,...,m1+m2(6) \qquad 式5称为目标函数，对应目标函数求解即为最优解。式6称为约束条件（包含等式约束和非等式约束）。
\qquad 从数学角度上，当目标函数获得最优解时，其必要条件为 ∂ F ( x ∗ ) ∂ x 1 = 0 , . . . ∂ F ( x ∗ ) ∂ x n = 0. ( 7 ) \frac{\partial F(x^{*})}{\partial x_{1}}=0,\\ ...\\ \frac{\partial F(x^{*})}{\partial x_{n}}=0.\qquad(7) ∂x1∂F(x∗)=0,...∂xn∂F(x∗)=0.(7) \qquad 此时对应的解为全局最小值或者局部最小值。在实际的运算过程中，同时获得n个方程的解较为困难(非凸函数)，因此使用下降法解决该类问题。
\qquad 下降算法伪代码：
1 任 意 选 择 初 始 点 x ( 0 ) ∈ R n ， 设 置 常 数 k 1\ 任意选择初始点x^{(0)}\in\mathbb{R}^{n}，设置常数k 1 任意选择初始点x(0)∈Rn，设置常数k
2 在 x k 点 选 择 下 降 方 向 ( 向 量 ) d ( k ) 2\ 在x_{k}点选择下降方向(向量)d^{(k)} 2 在xk点选择下降方向(向量)d(k)
3 在 此 方 向 上 选 择 步 长 α ( k ) 3\ 在此方向上选择步长\alpha^{(k)} 3 在此方向上选择步长α(k)
4 获 得 更 新 位 置 x ( k + 1 ) ← x ( k ) + α ( k ) d ( k ) 4\ 获得更新位置x^{(k+1)}\leftarrow x^{(k)}+\alpha^{(k)}d^{(k)} 4 获得更新位置x(k+1)←x(k)+α(k)d(k)
5 当 ∣ ∣ x ( k + 1 ) − x ( k ) ∣ ∣ < ε ≈ 0 时 ， x ( k + 1 ) 即 为 所 求 ， 否 则 ， 返 回 步 骤 1 5\ 当||x^{(k+1)}-x^{(k)}||<\varepsilon\approx0时，x^{(k+1)}即为所求，否则，返回步骤1 5 当∣∣x(k+1)−x(k)∣∣<ε≈0时，x(k+1)即为所求，否则，返回步骤1
\qquad 当使用的方法为牛顿下降法时，对应的 d k d^{k} dk选择为:
d ( k ) T = − ∇ F ( x ( k ) ) = − ( ∂ F ( x ( k ) ) ∂ x 1 ( k ) , . . . , ∂ F ( x ( k ) ) ∂ x n ( k ) ) ( 8 ) d^{(k)^{T}}=-\nabla F(x^{(k)})=-(\frac{\partial F(x^{(k)})}{\partial x_{1}^{(k)}},...,\frac{\partial F(x^{(k)})}{\partial x_{n}^{(k)}})\qquad(8) d(k)T=−∇F(x(k))=−(∂x1(k)∂F(x(k)),...,∂xn(k)∂F(x(k)))(8) \qquad 下降方法为牛顿法时， d ( k ) d^{(k)} d(k)选择为：
d ( k ) T = − [ ∇ 2 F ( x ( k ) ) ] − 1 ∇ F ( x ( k ) ) , ( 9 ) d^{(k)^{T}}=-[\nabla^{2}F(x^{(k)})]^{-1}\nabla F(x^{(k)}),\qquad(9) d(k)T=−[∇2F(x(k))]−1∇F(x(k)),(9)其中， ∇ 2 F ( x ( k ) ) \nabla^{2}F(x^{(k)}) ∇2F(x(k))是 F ( x ( k ) ) F(x^{(k)}) F(x(k))的Hessian矩阵。
∇ 2 F ( x ) = [ ∂ 2 F ∂ x 1 2 ⋯ ∂ 2 F ∂ x 1 ∂ x n ⋮ ⋱ ⋮ ∂ 2 F ∂ x n ∂ x 1 ⋯ ∂ 2 F ∂ x n 2 ] ( 10 ) \nabla^{2}F(x)=\begin{bmatrix} \frac{\partial^{2} F}{\partial x_{1}^{2}} & \cdots & \frac{\partial^{2} F}{\partial x_{1}\partial x_{n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial^{2} F}{\partial x_{n}\partial x_{1}} & \cdots & \frac{\partial^{2} F}{\partial x_{n}^{2}} \end{bmatrix}\qquad(10) ∇2F(x)=⎣⎢⎢⎡∂x12∂2F⋮∂xn∂x1∂2F⋯⋱⋯∂x1∂xn∂2F⋮∂xn2∂2F⎦⎥⎥⎤(10)
\qquad 位置点的最优化问题来源于最短信箱距离。图中圆圈代表信箱位置，其所对应的区域(泰森多边形)中的点为到信箱最短距离的点(对应所在区域的居民)。找到合适的信箱位置，使得居民取信的总体距离最短。
\qquad 将该问题使用数学方法描述为：
F ( x 1 , . . . , x n ) = ∑ i = 1 n ∫ V i f ( ∣ ∣ x − x i ∣ ∣ 2 ) ϕ ( x ) d x ( 11 ) F(x_{1},...,x_{n})=\sum_{i=1}^{n}\int_{V_{i}}f(||x-x_{i}||^{2})\phi(x)dx\qquad(11) F(x1,...,xn)=i=1∑n∫Vif(∣∣x−xi∣∣2)ϕ(x)dx(11) \qquad 其中，最简单的代价函数为 f ( ∣ ∣ x − x i ∣ ∣ 2 ) = c ∣ ∣ x − x i ∣ ∣ 2 = c ∣ ∣ x − x i ∣ ∣ f(||x-x_{i}||^{2})=c\sqrt{||x-x_{i}||^{2}}=c||x-x_{i}|| f(∣∣x−xi∣∣2)=c∣∣x−xi∣∣2=c∣∣x−xi∣∣， ϕ ( x ) \phi(x) ϕ(x)为所对应区域的密度函数，代价函数即可代表该区域居民取信总的消耗。求解代价函数的最小值(最小的消耗)即可表示为：
m i n x 1 , . . . x n ∑ i = 1 n ∫ V i f ( ∣ ∣ x − x i ∣ ∣ 2 ) ϕ ( x ) d x ( 12 ) \mathop{min}\limits_{x_{1},...x_{n}}\sum_{i=1}^{n}\int_{V_{i}}f(||x-x_{i}||^{2})\phi(x)dx\qquad(12) x1,...xnmini=1∑n∫Vif(∣∣x−xi∣∣2)ϕ(x)dx(12) \qquad 由此问题是非凸问题，使用之前的搜索法解决该问题。首先是对该问题进行求导。假设 V \mathcal{V} V为由 { x i , . . . , x i , . . . , x n } \{x_{i},...,x_{i},...,x_{n}\} {xi,...,xi,...,xn}生成的泰森多边形图， V ′ \mathcal{V}^{'} V′为由 { x i , . . . , x i + δ x i , . . . , x n } \{x_{i},...,x_{i}+\delta x_{i},...,x_{n}\} {xi,...,xi+δxi,...,xn}生成的泰森多边形图， V i V_{i} Vi是由 V \mathcal{V} V中第i个生成点生成的泰森多边形， V i ′ V_{i}^{'} Vi′是由 V ′ \mathcal{V}^{'} V′中第i个生成点生成的泰森多边形。 V j , j ∈ J i V_{j},j\in J_{i} Vj,j∈Ji为 V i V_{i} Vi的相邻的泰森多边形。则：
Δ F = F ( x 1 , . . . , x i + δ x i , . . . , x n ) − F ( x 1 , . . . , x i , . . . , x n ) = ∫ V i ′ f ( ∣ ∣ x i + δ x i − x ∣ ∣ 2 ) ϕ ( x ) d x − ∫ V i f ( ∣ ∣ x i − x ∣ ∣ 2 ) ϕ ( x ) d x + ∑ j ∈ J i [ ∫ V j ′ f ( ∣ ∣ x j − x ∣ ∣ 2 ) ϕ ( x ) d x − ∫ V j f ( ∣ ∣ x j − x ∣ ∣ 2 ) ϕ ( x ) d x ] ( 13 ) \Delta F=F(x_{1},...,x_{i}+\delta x_{i},...,x_{n})-F(x_{1},...,x_{i},...,x_{n})\\ =\int_{V_{i}^{'}}f(||x_{i}+\delta x_{i}-x||^{2})\phi(x)dx-\int_{V_{i}}f(||x_{i}-x||^{2})\phi(x)dx\\ +\sum_{j\in J_{i}}[\int_{V_{j}^{'}}f(||x_{j}-x||^{2})\phi(x)dx-\int_{V_{j}}f(||x_{j}-x||^{2})\phi(x)dx]\qquad(13) ΔF=F(x1,...,xi+δxi,...,xn)−F(x1,...,xi,...,xn)=∫Vi′f(∣∣xi+δxi−x∣∣2)ϕ(x)dx−∫Vif(∣∣xi−x∣∣2)ϕ(x)dx+j∈Ji∑[∫Vj′f(∣∣xj−x∣∣2)ϕ(x)dx−∫Vjf(∣∣xj−x∣∣2)ϕ(x)dx](13)
\qquad 其中方程区间组成为 V i = ( V i ∩ V i ′ ) ∪ ( V i \ V i ∩ V i ′ ) V_{i}=(V_{i}\cap V_{i}^{'})\cup(V_{i}\verb|\|V_{i}\cap V_{i}^{'}) Vi=(Vi∩Vi′)∪(Vi\Vi∩Vi′)， V i ′ = ( V i ∩ V i ′ ) ∪ ( V i ′ \ V i ∩ V i ′ ) V_{i}^{'}=(V_{i}\cap V_{i}^{'})\cup(V_{i}^{'}\verb|\|V_{i}\cap V_{i}^{'}) Vi′=(Vi∩Vi′)∪(Vi′\Vi∩Vi′)， V j = ( V j ∩ V j ′ ) ∪ ( V i ′ ∩ V j ) V_{j}=(V_{j}\cap V_{j}^{'})\cup(V_{i}^{'}\cap V_{j}) Vj=(Vj∩Vj′)∪(Vi′∩Vj)和 V j ′ = ( V j ∩ V j ′ ) ∪ ( V i ∩ V j ′ ) V_{j}^{'}=(V_{j}\cap V_{j}^{'})\cup(V_{i}\cap V_{j}^{'}) Vj′=(Vj∩Vj′)∪(Vi∩Vj′)，式13可以改写为：
Δ F = ∫ V i ′ ∩ V i [ f ( ∣ ∣ x i + δ x i − x ∣ ∣ 2 ) − f ( ∣ ∣ x i − x ∣ ∣ 2 ) ] ϕ ( x ) d x + ∫ V i ′ \ V i ∩ V i ′ f ( ∣ ∣ x i + δ x i − x ∣ ∣ 2 ) ϕ ( x ) d x − ∫ V i \ V i ∩ V i ′ f ( ∣ ∣ x i − x ∣ ∣ 2 ) ϕ ( x ) d x + ∑ j ∈ J i [ ∫ V j ′ ∩ V i f ( ∣ ∣ x j − x ∣ ∣ 2 ) ϕ ( x ) d x − ∫ V j ∩ V i ′ f ( ∣ ∣ x j − x ∣ ∣ 2 ) ϕ ( x ) d x ] ( 14 ) \Delta F=\int_{V_{i}^{'}\cap V_{i}}[f(||x_{i}+\delta x_{i}-x||^{2})-f(||x_{i}-x||^{2})]\phi(x)dx\\ +\int_{V_{i}^{'}\verb|\|V_{i}\cap V_{i}^{'}}f(||x_{i}+\delta x_{i}-x||^{2})\phi(x)dx-\int_{V_{i}\verb|\|V_{i}\cap V_{i}^{'}}f(||x_{i}-x||^{2})\phi(x)dx\\ +\sum_{j\in J_{i}}[\int_{V_{j}^{'}\cap V_{i}}f(||x_{j}-x||^{2})\phi(x)dx-\int_{V_{j}\cap V_{i}^{'}}f(||x_{j}-x||^{2})\phi(x)dx]\qquad(14) ΔF=∫Vi′∩Vi[f(∣∣xi+δxi−x∣∣2)−f(∣∣xi−x∣∣2)]ϕ(x)dx+∫Vi′\Vi∩Vi′f(∣∣xi+δxi−x∣∣2)ϕ(x)dx−∫Vi\Vi∩Vi′f(∣∣xi−x∣∣2)ϕ(x)dx+j∈Ji∑[∫Vj′∩Vif(∣∣xj−x∣∣2)ϕ(x)dx−∫Vj∩Vi′f(∣∣xj−x∣∣2)ϕ(x)dx](14) \qquad 由几何变化关系得：
V j ′ \ ( V i ∩ V i ′ ) = ∑ j ∈ J i V i ′ ∩ V j , V j \ ( V i ∩ V i ′ ) = ∑ j ∈ J i V i ∩ V j ′ ( 15 ) V_{j}^{'}\verb|\|(V_{i}\cap V_{i}^{'})=\sum_{j\in J_{i}}V_{i}^{'}\cap V_{j},V_{j}\verb|\|(V_{i}\cap V_{i}^{'})=\sum_{j\in J_{i}}V_{i}\cap V_{j}^{'}\qquad(15) Vj′\(Vi∩Vi′)=j∈Ji∑Vi′∩Vj,Vj\(Vi∩Vi′)=j∈Ji∑Vi∩Vj′(15)化简为：
Δ F = ∫ V i ′ ∩ V i [ f ( ∣ ∣ x i + δ x i − x ∣ ∣ 2 ) − f ( ∣ ∣ x i − x ∣ ∣ 2 ) ] ϕ ( x ) d x + ∑ j ∈ J i ∫ V i ′ ∩ V j ( f ( ∣ ∣ x i + δ x i − x ∣ ∣ 2 ) − f ( ∣ ∣ x j − x ∣ ∣ 2 ) ) ϕ ( x ) d x + ∑ j ∈ J i [ ∫ V j ′ ∩ V i ( f ( ∣ ∣ x j − x ∣ ∣ 2 ) − f ( ∣ ∣ x i − x ∣ ∣ 2 ) ϕ ( x ) d x ( 16 ) \Delta F=\int_{V_{i}^{'}\cap V_{i}}[f(||x_{i}+\delta x_{i}-x||^{2})-f(||x_{i}-x||^{2})]\phi(x)dx\\ +\sum_{j\in J_{i}}\int_{V_{i}^{'}\cap V_{j}}(f(||x_{i}+\delta x_{i}-x||^{2})-f(||x_{j}-x||^{2}))\phi(x)dx\\ +\sum_{j\in J_{i}}[\int_{V_{j}^{'}\cap V_{i}}(f(||x_{j}-x||^{2})-f(||x_{i}-x||^{2})\phi(x)dx\qquad(16) ΔF=∫Vi′∩Vi[f(∣∣xi+δxi−x∣∣2)−f(∣∣xi−x∣∣2)]ϕ(x)dx+j∈Ji∑∫Vi′∩Vj(f(∣∣xi+δxi−x∣∣2)−f(∣∣xj−x∣∣2))ϕ(x)dx+j∈Ji∑[∫Vj′∩Vi(f(∣∣xj−x∣∣2)−f(∣∣xi−x∣∣2)ϕ(x)dx(16) \qquad 由 l i m δ x → 0 ( V j ′ ∩ V i ) = 0 , l i m δ x → 0 ( V j ∩ V i ′ ) = 0 \mathop{lim}\limits_{\delta x\rightarrow0}(V_{j}^{'}\cap V_{i})=0,\mathop{lim}\limits_{\delta x\rightarrow0}(V_{j}\cap V_{i}^{'})=0 δx→0lim(Vj′∩Vi)=0,δx→0lim(Vj∩Vi′)=0得：
Δ F = ∫ V i ′ ∩ V i [ f ( ∣ ∣ x i + δ x i − x ∣ ∣ 2 ) − f ( ∣ ∣ x i − x ∣ ∣ 2 ) ] ϕ ( x ) + O ∣ ∣ δ x i ∣ ∣ 2 d x ( 17 ) \Delta F=\int_{V_{i}^{'}\cap V_{i}}[f(||x_{i}+\delta x_{i}-x||^{2})-f(||x_{i}-x||^{2})]\phi(x)+O||\delta x_{i}||^{2}dx\qquad(17) ΔF=∫Vi′∩Vi[f(∣∣xi+δxi−x∣∣2)−f(∣∣xi−x∣∣2)]ϕ(x)+O∣∣δxi∣∣2dx(17) ∂ F ∂ x i k = l i m δ x i k → 0 Δ F δ x i k = l i m δ x i k → 0 [ ∫ V i ′ ∩ V i f ( ∣ ∣ x i + δ x i − x ∣ ∣ 2 ) − f ( ∣ ∣ x i − x ∣ ∣ 2 ) δ x i k ϕ ( x ) d x + O ∣ ∣ δ x i ∣ ∣ 2 δ x i k ] , k = 1 , 2... ( 18 ) \frac{\partial F}{\partial x_{i_{k}}}=\mathop{lim}\limits_{\delta x_{i_{k}}\rightarrow0}\frac{\Delta F}{\delta x_{i_{k}}}=\mathop{lim}\limits_{\delta x_{i_{k}}\rightarrow0}[\int_{V_{i}^{'}\cap V_{i}}\frac{f(||x_{i}+\delta x_{i}-x||^{2})-f(||x_{i}-x||^{2})}{\delta x_{i_{k}}}\phi(x)dx+\frac{O||\delta x_{i}||^{2}}{\delta x_{ik}}],k=1,2...\qquad(18) ∂xik∂F=δxik→0limδxikΔF=δxik→0lim[∫Vi′∩Viδxikf(∣∣xi+δxi−x∣∣2)−f(∣∣xi−x∣∣2)ϕ(x)dx+δxikO∣∣δxi∣∣2],k=1,2...(18) \qquad 所以一阶导函数为：
∂ F ∂ x i k = ∫ V i 2 ( x i k − x k ) f ′ ( ∣ ∣ x i − x ∣ ∣ 2 ) ϕ ( x ) d x , k = 1 , 2... ( 19 ) \frac{\partial F}{\partial x_{i_{k}}} =\int_{V_{i}}2(x_{i_{k}}-x_{k})f^{'}(||x_{i}-x||^{2})\phi(x)dx,k=1,2...\qquad(19) ∂xik∂F=∫Vi2(xik−xk)f′(∣∣xi−x∣∣2)ϕ(x)dx,k=1,2...(19) \qquad 选择合适的步长 α \alpha α，对应不同概率密度函数 ϕ ( x ) \phi(x) ϕ(x)最优位置估计为：
参考文献
1.Centroidal Voronoi Tessellations:Applications and Algorithms.Max Gunzburger
2.Spatial Tessellations:Concepts and Applications of Voronoi Diagrams.charp9.Vic Barnett, Noel A. C. Cressie
![[转载]泰森多边形（泰森图）](https://img-blog.csdnimg.cn/img_convert/0664d8b38af26c2a5523247bbcbb85f2.png)
