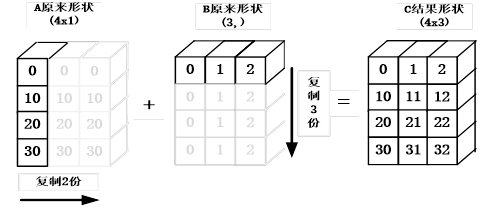
A. 计算

一、计算

1. 计算
   · 对象：规律，技巧
   · 目标：高效，低耗
2. computer science – computing science
3. 例子
   · 绳索计算机：勾股定理找垂线
   · 尺规计算机：等分点—子程序

二、算法

1. 算法

1. 计算 = 信息处理 = 借助某种工具，遵照一定规则，以明确而机械的形式进行
2. 计算模型 = 计算机 = 信息处理工具
3. 算法，即特定计算模型下，旨在解决特定问题的指令序列
   · 输入：待处理的信息（问题）
   · 输出：经处理的信息（答案）
   · 正确性
   · 确定性：任一算法都可以描述为一个由基本操作组成的序列
   · 可行性：每一基本操作都可实现，且在常数时间内完成
   · 有穷性

2. 有穷性

Hailstone

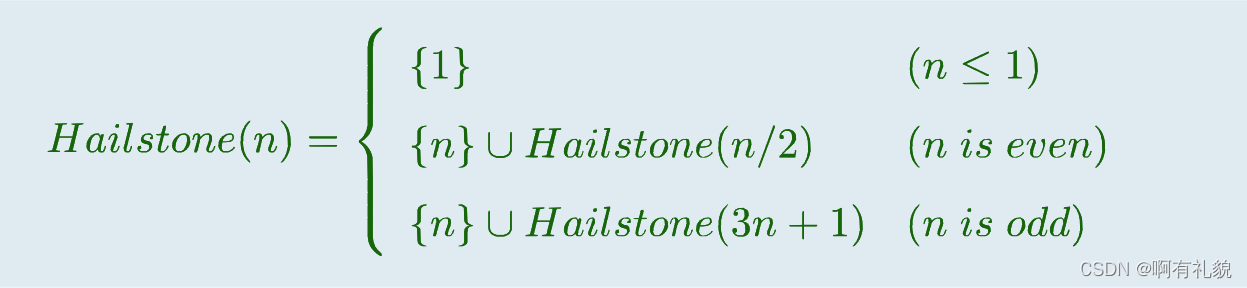
3. 好算法

1. 特性：正确、健壮、可读、效率
2. Algorithms + Data Structures = Programs
3. （Algorithms + Data Structures）* Efficiency = Computation

三、作业

1. Hailstone问题（又名3n+1问题）中Hailstone(n)的计算程序是：不能确定是否存在n，使程序无法终止
2. 判断一个算法是否是一个“好算法”，最重要的一条性质是：efficiency 效率

B. 计算模型

一、 算法

1. 性能测度：measure

• 引入理想、统一、分层次的尺度
• 运用该尺度，以测量DSA的性质

2. 问题规模：划分等价类

1. 算法分析的两个方面：正确、成本（运行时间 + 所需存储空间）
2. T_A§ = 算法A求解问题实例P的计算成本
3. 归纳、概括 —— 划分等价类

3. 最坏情况

1. 令T_A(n) = 用算法A求解某一问题为n的实例，所需的计算成本
2. T(n) = max { T§ | |p|=n}

4. 理想模型

1. 不同的算法：规模、类型；同一算法：不同程序员、语言、编译器、体系结构、操作系统等
2. 关键：抽象出一个理想的平台或模型

二、图灵机

• 构成部件： Tape、 Alphabet、Head、State状态
• 转换函数： Transition Function: (q, c; d, L/R, p)

三、RAM模型

1. RAM（Random Access Machine）
   T(n) = 算法为求解规模为n的问题，所需执行的基本操作次数
2. 例子Floor Division
   · 时间成本：各条指令执行次数之总和
   · 能够客观度量算法的执行时间

四、作业

1. 以下哪项不是图灵机的组成要件？tape of finite length 有限长的纸带（作为一个理想计算模型，图灵机的纸带是两端无线延伸的无限长纸带）
2. RAM模型与图灵机模型的区别在于图灵机的存储空间无限，而RAM的存储空间有限。False 错（RAM模型中寄存器的总数没有限制，它与图灵机是等价的）

C. 渐进复杂度

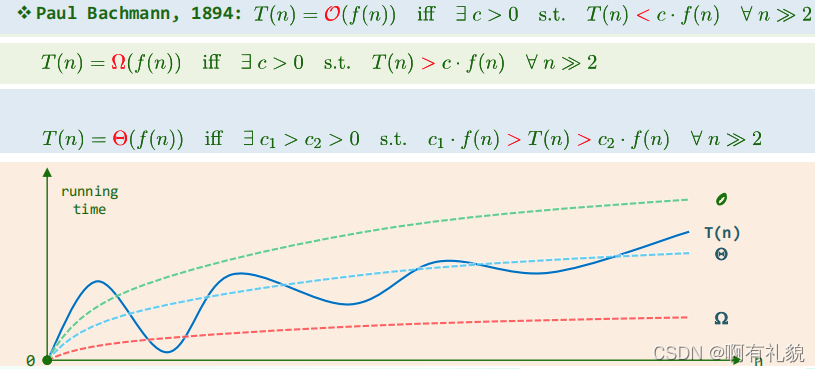
一、渐进分析-Big-O 记号

1. 问题规模足够大之后，计算成本的增长趋势
2. Big-O notation
   

二、多项式

1. 求解问图

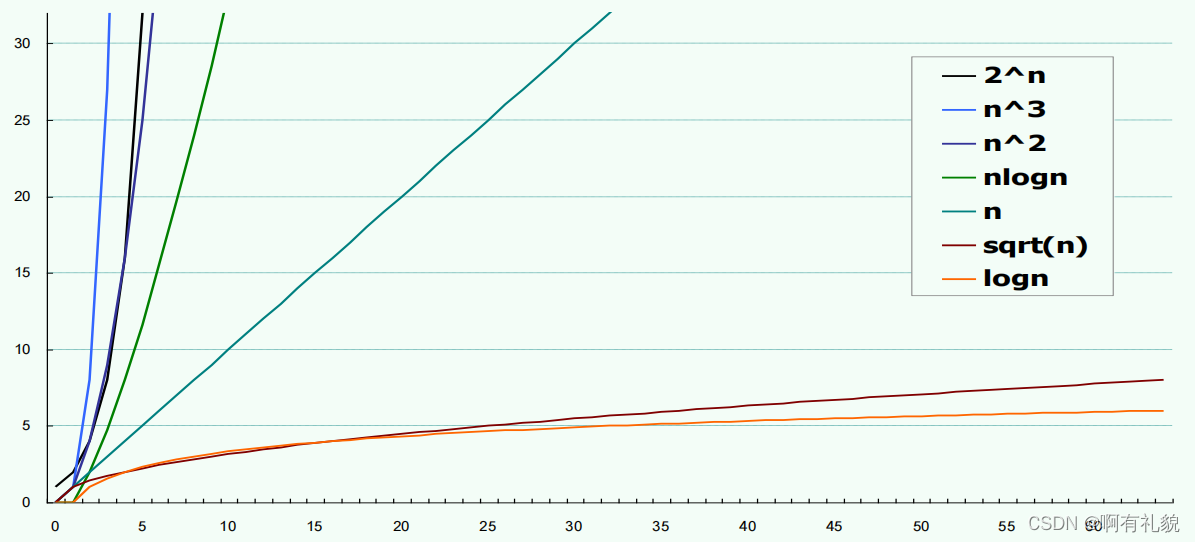
易解问题：线性（linear function）：所有O(n)类函数

1. constant O(1)：不含转向（循环、调用、递归等），必顺序执行
2. poly-log O(log ^c n) = O(n ^c)，c>0：复杂度无限接近于常数，对数底数、常底数、常数次幂无所谓
3. polynomial O(n ^c)：多项式a_kn^k + a_k-1n^k-1 + …… + a₂² + a₁n + a₀ = O(n^k)， a_k > 0
   难解问题：指数
4. exponential O(2ⁿ)：成本增长极快，从O(n ^c) 到 O(2ⁿ)，是从有效增长到无效增长的分水岭

2. 增长速度

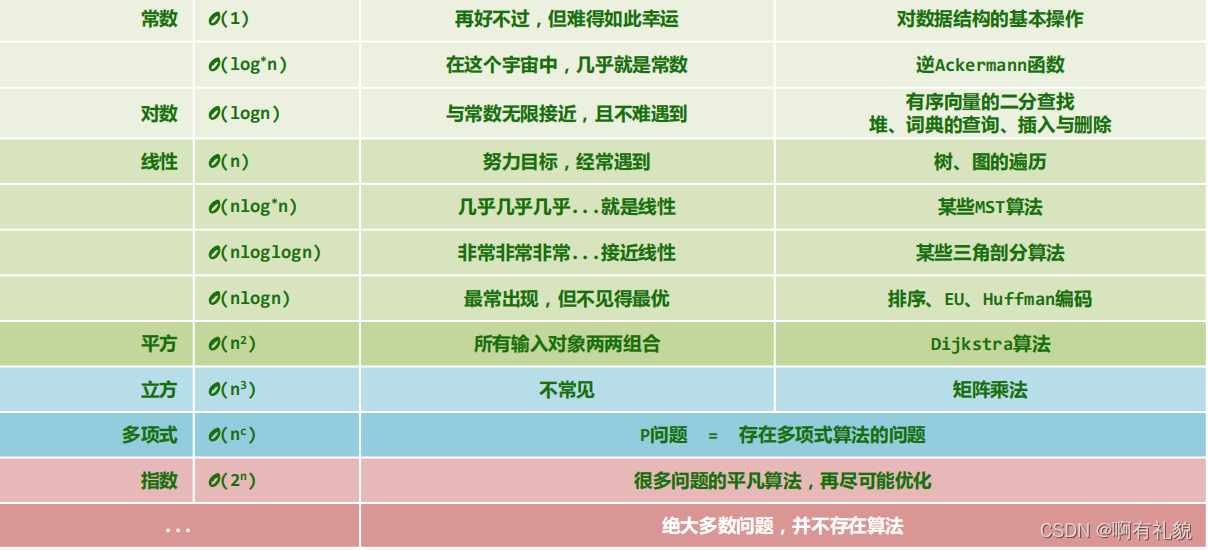
3. 层次级别

三、作业

1. 在大O记号的意义下，以下哪一项与O(m³)相等？(m不是常数) O(m³ + 2000n² + 1000n)

D. 复杂度分析

一、级数

1. 算法分析

• 主要任务：正确性（不变性 * 单调性） + 复杂度
• 复杂度分析的主要方法：
  · 迭代：级数求和
  · 递归： 递归跟踪 + 递推方程
  · 实用：猜测 + 验证

2. 级数

1. 算术级数：与末项平方同阶
2. 幂方级数：比幂次高出一阶
3. 几何级数：与末项同阶
4. 收敛级数：O(1)
5. 不收敛但有限：
   

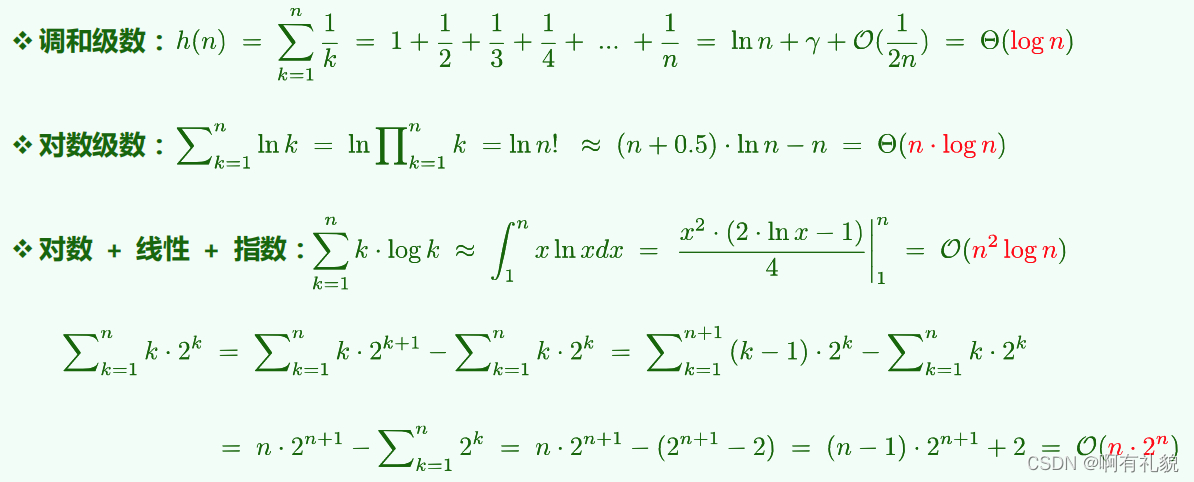
二、 迭代

三、正确性证明

以冒泡排序为例：

1. 不变性：经k轮扫描交换后，最大的k个元素必然就位
2. 单调性：经k轮扫描交换后，问题规模缩减至n-k
3. 正确性：经至多n轮扫描后，算法必然终止，且能给出正确解答

四、封底估算（Back-Of-Envelope Calculation）

五、作业

1. Which of the following equations is wrong? 下列对应关系中错误的是：1+ 1/2 +1/3 + …… + 1/n = O(nlogn) （正确O(logn)）
2. x=n; y=1; while( x >= (y-1)*(y+1)) y++;The complexity of the program above is 以上程序的时间复杂度为：不大于n的完全平方根加1的最大整数。
3. True or false: In bubble sort, the size of the problem is reduced to k after k rounds of sweep & swap.判断：经过k轮扫描交换后，起泡排序程序会将问题规模缩减至k。 False错（n-k）

E. 迭代与递归

迭代乃人工，递归方神通

一、减而治之Decrease-and-conquer

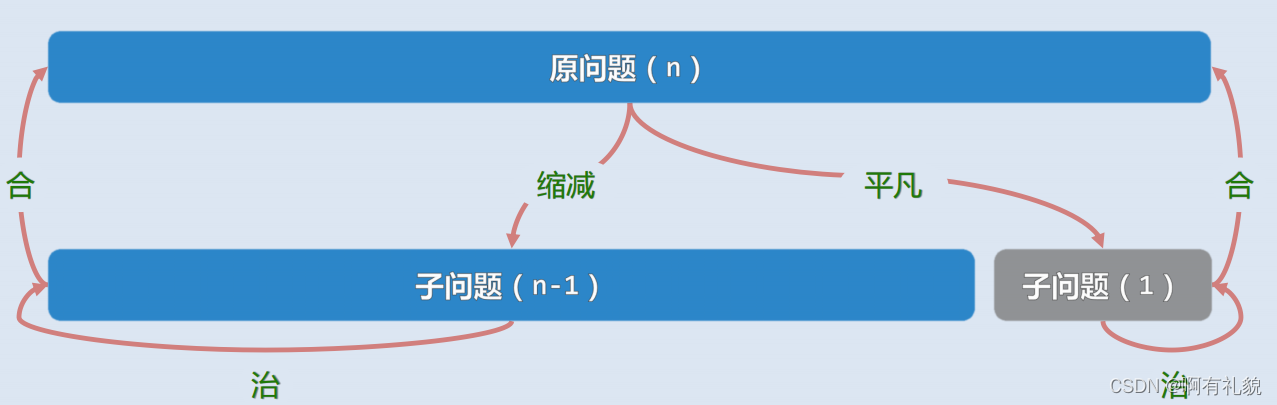
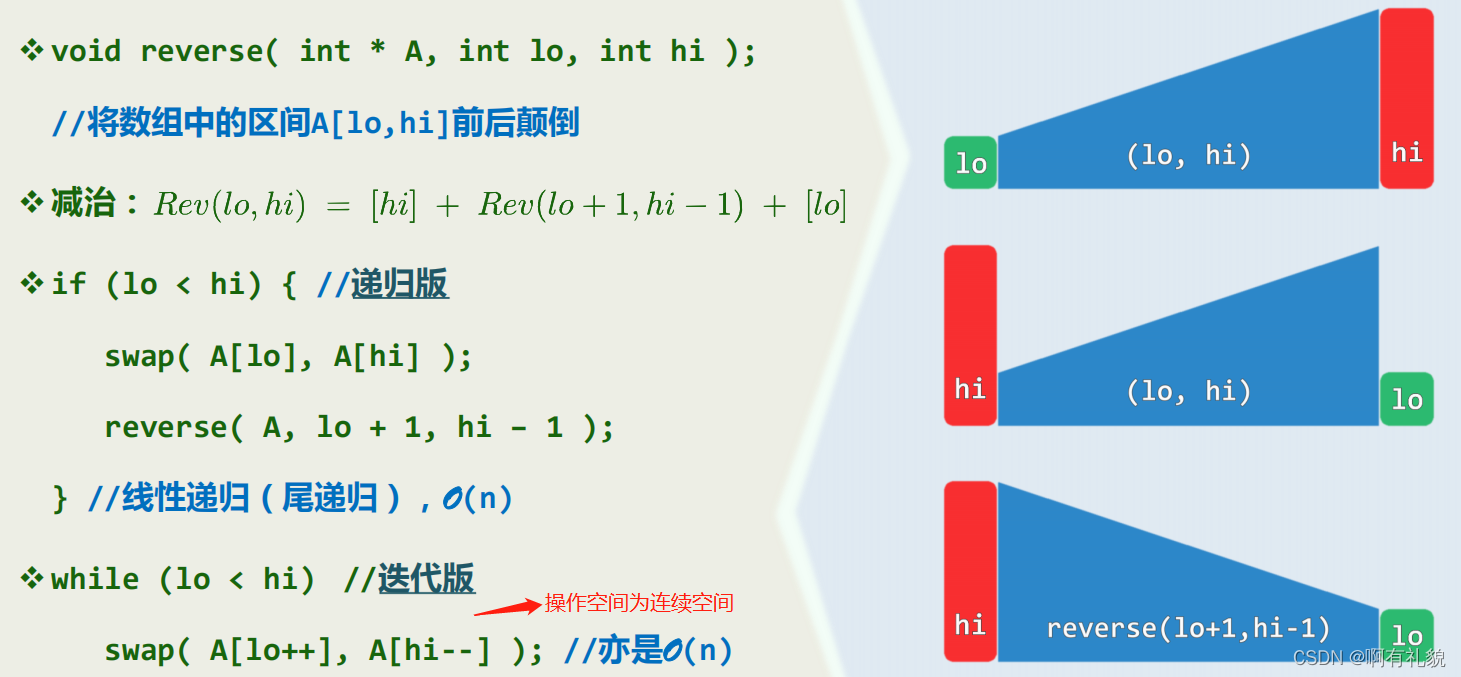
二、递归跟踪（recursion trace）

• 算法时间：检查每个递归实例，累计所需时间（调用语句本身，计入对应的子例）
• 线性递归：Linear Recursion —— O(n) T(n)=O(1)+n=O(n)
• 数组倒置：Reverse
  

三、分而治之Divide-and-conquer

四、大师定理/主定理/Master Theorem

五、作业

1.True or false: To apply decrease-and-conquer, we divide the original problem into two degenerated sub-problems, solve them, and merge their solutions. 判断：减而治之的思想是：将问题划分为两个平凡的子问题，分别求解子问题，来得到原问题的解 False错
2. Li Lei and Han Meimei have different opinions regarding the linear time complexity in the video lecture.对于视频中线性递归的时间复杂度，A、B两位同学有不同的看法。Li Lei aggrees to the video, the complexity is O(n) because there are n instances each requiring O(1) execution time. A同学赞同视频中的算法，由于单个递归实例需要O（1）时间完成，共有n个实例，所以整个算法的复杂度是O（n）However, Han Meimei believes the time for sum（A,n) to be O(n) instead of O(1), since it’s still executing even when calling sum(A,n-1), leading to a total time complexity of （. You agree with 但B同学认为，当sum（A,n）函数中调用sum(A,n-1)时，sum(A,n)仍在执行，因此sum（A,n）的完成时间不是O(1)而是O（n），依此计算，整个算法的复杂度应该为（）。请问哪位同学对了？ Li Lei A同学
3. In the video lecture we see a comment in the code: “Two base cases are required”. What does it refer to? 视频里代码注释中“需要两个递归基”的含义是 The sequence of recursive callls is terminated when the problem size is reduced to either 0 or 1. 在问题规模缩减为0或1时，停止递归
4. 判断：用分而治之的思想来解决长度为n的数组的求和问题（n足够大），递归实例的数目会比用减而治之的方法少。 错

F. 动态规划

一、fibonacci数

1. 递归版fibonacci数低效根源：各递归实例均被大量重复地调用
2. 迭代
   · memoization（制表备查）
   · 颠倒计算方法：自底向上递归

二、LCS(Longest Common Sbusequence)最长公共子序列

• 递归：最好O(n+m); 最差O(2ⁿ)
  1. 递归基：若n=-1或m=-1，则取做空序列
  2. 减而治之：若A[n] = ‘X’ = B[m]，则LCS(n-1, m-1)+‘X’
  3. 分而治之：A[n] ≠ B[m]，则LCS(n, m-1)与LCS(n-1, m)中取更长者
• 动态规划—迭代：O(n*m)
• 单调性：每经过一次比对，至少一个序列的长度缩短一个单位

三、作业

1. The naive way of computing fib(n) recursively leads to a time complexity of 直接用定义以递归的方式计算fib(n)的时间复杂度是：O(2ⁿ)
2. With a regular computer, computing fib(100) naively using recursion would cost (no need to consider overflow). 以现在普通计算机的速度，直接用定义以递归的方式计算fib(100)需要多少时间（不考虑溢出）:much longer than your lifetime. 这辈子看不到啦
3. For the staircase problem in the video lecture, how many different ways can get you from the first step to the eighth. 对于视频中的上台阶问题（从第一层开始），上到第8层共有多少种不同的走法：34
4. The time and space complexities for computing fib(n) with dynamic programming are 用动态规划计算fib(n)的时间、空间复杂度分别为:θ(n)，θ(1)
5. The length of the LCS between “program” and “algorithm” is program 和 algorithm的LCS长度为:3
6. LCS(x,y) is defined to be the length of the LCS between strings x and y. LCS(“program”, “algorithm”) = LCS(x,y)表示字符串x,y最长公共子序列长度，则LCS（“program”, “algorithm”）= LCS（“progra”, “algorith”） + 1
7. Checkout the Demo in the video lecture (the download link is on the right side of the “Course” page, or in 01-f-6). Which tool was used to write the demo?下载并使用视频中的Demo（下载链接在“课程信息”右侧，01-f-6里也有），它是用什么做的？MS Excel
8. Computing the LCS using dynamic programming leads to a time complexity of (m and n are the lengths of the input strings) 用动态规划求解输入序列长度分别为m,n的LCS问题，时间复杂度为：θ(m*n)

XA. 局限(缓存)

一、就地循环移位：

1. 蛮力版O(n*k)：反复以1为间距循环佐移
2. 迭代版O(n)：同余类（考虑是否互素）
3. 倒置版O(3n)：cache连续访问

二、作业

1. 如下图
   
2. Which of the following functions grows fastest asymptotically?下列函数渐进增长速度最快的是：n/log₂(n)
3. . Given the following three functions: 以下是三个函数：Their time complexities are: 它们的时间复杂度分别为：
4. The following recursive function is for reversing array A[lo, hi]以下递归函数实现数组A[lo, hi]的倒置：What is the time complexity of reverse(A, 0, n-1), for reversing an array of length n?调用reverse(A, 0, n-1)以倒置长度为n的数组，算法的时间复杂度为：
   
5. V={11, 23, 19, 7, 17, 5, 3, 13, 2, 29} When sorting V using bubble sort, what is the value of V[8] after two rounds of sweep & swap?对V进行起泡排序，两趟扫描交换后V[8] = 23