文章目录

第1章实践基础
- 1.1 如何运行本书的代码
- - 1.1.1 本地运行
  - - 1.1.1.1 环境准备
    - 1.1.1.2 快速安装
  - 1.1.2 AI Studio运行
- 1.2 张量
- - 1.2.1 创建张量
  - - 1.2.1.1 指定数据创建张量
    - 1.2.1.2 指定形状创建
    - 1.2.1.3 指定区间创建
  - 1.2.2 张量的属性
  - - 1.2.2.1 张量的形状
    - 1.2.2.2 形状的改变
    - 1.2.2.3 张量的数据类型
    - 1.2.2.4 张量的设备位置
  - 1.2.3 张量与Numpy数组转换
  - 1.2.4 张量的访问
  - - 1.2.4.1 索引和切片
    - 1.2.4.2 访问张量
    - 1.2.4.3 修改张量
  - 1.2.5 张量的运算
  - - 1.2.5.1 数学运算
    - 1.2.5.2 逻辑运算
    - 1.2.5.3 矩阵运算
    - 1.2.5.4 广播机制
    - - 广播机制的条件
      - 广播机制的计算规则
- 1.3 算子
- - 1.3.1 算子定义
  - - 1.3.1.1 加法算子
    - - 前向计算
      - 反向计算
    - 1.3.1.2 乘法算子
    - 1.3.1.3 指数算子
  - 1.3.2 自动微分机制
  - - 1.3.2.1 前向执行
    - 1.3.2.2 反向执行
  - 1.3.3 预定义的算子
  - 1.3.4 本书中实现的算子
  - 1.3.5 本书中实现的优化器
- 1.4 本书中实现的DataSet类
- - 1.4.1 数据集
  - 1.4.2 Dataset类
- 1.5 本书中使用的Runner类
- 1.6 小结
- 1.7 课程链接

第1章实践基础

深度学习在很多领域中都有非常出色的表现，在图像识别、语音识别、自然语言处理、机器人、广告投放、医学诊断和金融等领域都有广泛应用。而目前深度学习的模型还主要是各种各样的神经网络。随着网络越来越复杂，从底层开始一步步实现深度学习系统变得非常低效，其中涉及模型搭建、梯度求解、并行计算、代码实现等多个环节。每一个环节都需要进行精心实现和检查，需要耗费开发人员很多的精力。为此，深度学习框架（也常称为机器学习框架）应运而生，它有助于研发人员聚焦任务和模型设计本身，省去大量而烦琐的代码编写工作，其优势主要表现在如下两个方面：

实现简单：深度学习框架屏蔽了底层实现，用户只需关注模型的逻辑结构，同时简化了计算逻辑，降低了深度学习入门门槛。
使用高效：深度学习框架具备灵活的移植性，在不同设备（CPU、GPU或移动端）之间无缝迁移，使得深度学习框架会使模型训练以及部署更高效。

本书使用飞桨框架作为实践的基础框架。飞桨（PaddlePaddle）框架是一套面向深度学习的基础训练和推理框架。飞桨于2016年正式开源，是主流深度学习开源框架中一款完全国产化的产品。目前，飞桨框架已经非常成熟并且易用，可以很好地支持本书的实践设计。

在讲解本书主要内容之前，本章先对实践环节的基础知识进行介绍，主要介绍以下内容：

张量（Tensor）：深度学习中表示和存储数据的主要形式。在动手实践机器学习之前，需要熟悉张量的概念、性质和运算规则，以及了解飞桨中张量的各种API。
算子（Operator）：构建神经网络模型的基础组件。每个算子有前向和反向计算过程，前向计算对应一个数学函数，而反向计算对应这个数学函数的梯度计算。有了算子，我们就可以很方便地通过算子来搭建复杂的神经网络模型，而不需要手工计算梯度。

此外，本章还汇总了在本书中自定义的一些算术、数据集以及轻量级训练框架Runner类。

1.1 如何运行本书的代码

笔记

本书涉及大量代码实践，通过运行代码理解如何构建模型及训练网络。本书中代码有两种运行方式：本地运行AI Studio运行。下面我们分别介绍两种运行方式的环境准备及操作方法。

1.1.1 本地运行

1.1.1.1 环境准备

本书代码基于Python语言与飞桨框架开发，如选择在本地运行请首先确认本机的操作系统、Python及pip版本是否满足飞桨支持的环境。目前飞桨支持的环境如下：

Linux 版本（64 bit）
- CentOS 7（GPU版本支持CUDA 10.1/10.2/11.0/11.1/11.2）
  - Ubuntu 16.04（GPU版本支持CUDA 10.1/10.2/11.0/11.1/11.2）
  - Ubuntu 18.04（GPU版本支持CUDA 10.1/10.2/11.0/11.1/11.2）
  - Ubuntu 20.04（GPU版本支持CUDA 10.1/10.2/11.0/11.1/11.2）
Python版本3.6/3.7/3.8/3.9（64 bit）
pip或pip3版本20.2.2或更高版本（64 bit）

可以使用如下命令查看本机的操作系统和位数信息：

uname -m && cat /etc/*release

使用如下命令确认Python版本是否为3.6/3.7/3.8/3.9:

python --version

使用如下命令确认pip版本是否满足要求：

python -m ensurepip
python -m pip --version

确认Python和pip是64bit版本，且处理器架构是x86_64（或称作x64、Intel 64、AMD64）架构。需要注意，目前飞桨不支持arm64架构。

python -c "import platform;print(platform.architecture()[0]);print(platform.machine())"

该命令第一行输出为“64bit”，第二行输出为“x86_64”“x64”或“AMD64”即符合要求。

1.1.1.2 快速安装

本书第1章内容使用CPU即可完成，无须其他硬件设备。但从第2章开始，建议使用支持CUDA的GPU，书中代码默认在32G RAM的Tesla V100上运行，如使用其他配置的GPU可适当调整模型训练参数或直接通过AI Studio平台运行代码。

笔记
在GPU上运行模型训练代码可以大幅缩短模型训练时间，但使用GPU并不是必需的。如果电脑没有GPU硬件设备，本书内代码在仅使用CPU的情况下仍可以跑通，只是模型训练所需时间会增加。在这种情况下，可以使用AI Studio平台的免费GPU算力运行代码。使用方法详见第1.1.2节。

目前推荐使用飞桨开源框架v2.2版本，后续可在飞桨官网查看最新稳定版本。通过如下命令安装CPU版本：

python -m pip install paddlepaddle==2.2.2 -i https://mirror.baidu.com/pypi/simple

通过如下命令安装GPU版本：

python -m pip install paddlepaddle-gpu==2.2.2 -i https://mirror.baidu.com/pypi/simple

默认GPU环境为CUDA 10.2，如需安装基于其他CUDA版本的飞桨框架，可在2.2.2后面加入版本后缀，比如CUDA 10.1版本的飞桨框架对应为paddlepaddle-gpu==2.2.2.post101。

动手练习1.1

使用python命令进入python解释器，输入import paddle，验证安装是否成功。
输入paddle.__version__验证版本安装是否正确。
输入paddle.utils.run_check()，如出现“PaddlePaddle is installed successfully!”，则说明已正确安装。

1.1.2 AI Studio运行

AI Studio是基于飞桨的人工智能学习与实训社区，提供免费的算力支持，本书的内容在AI Studio上提供配套的BML Codelab项目。BML Codelab是面向个人和企业开发者的AI开发工具，基于Jupyter提供了在线的交互式开发环境。

BML Codelab目前默认使用飞桨2.2.2版本，无须额外安装。如图1.1所示，通过选择“启动环境” $\rightarrow$ “基础版”即可在CPU环境下运行，选择“至尊版GPU”即可在32G RAM的Tesla V100上运行代码，至尊版GPU每天有8小时的免费使用时间。

图1.1 AI Studio项目运行环境选择

选择环境进入项目后，项目整体布局如图1.2所示。项目页面（Notebook）由侧边栏、菜单栏、快捷工具栏、状态监控栏和代码编辑区组成。这里我们重点介绍代码编辑区和快捷工具栏，其余边栏的使用方法可参见BML Codelab环境使用说明。

图1.2 BML Codelab项目布局

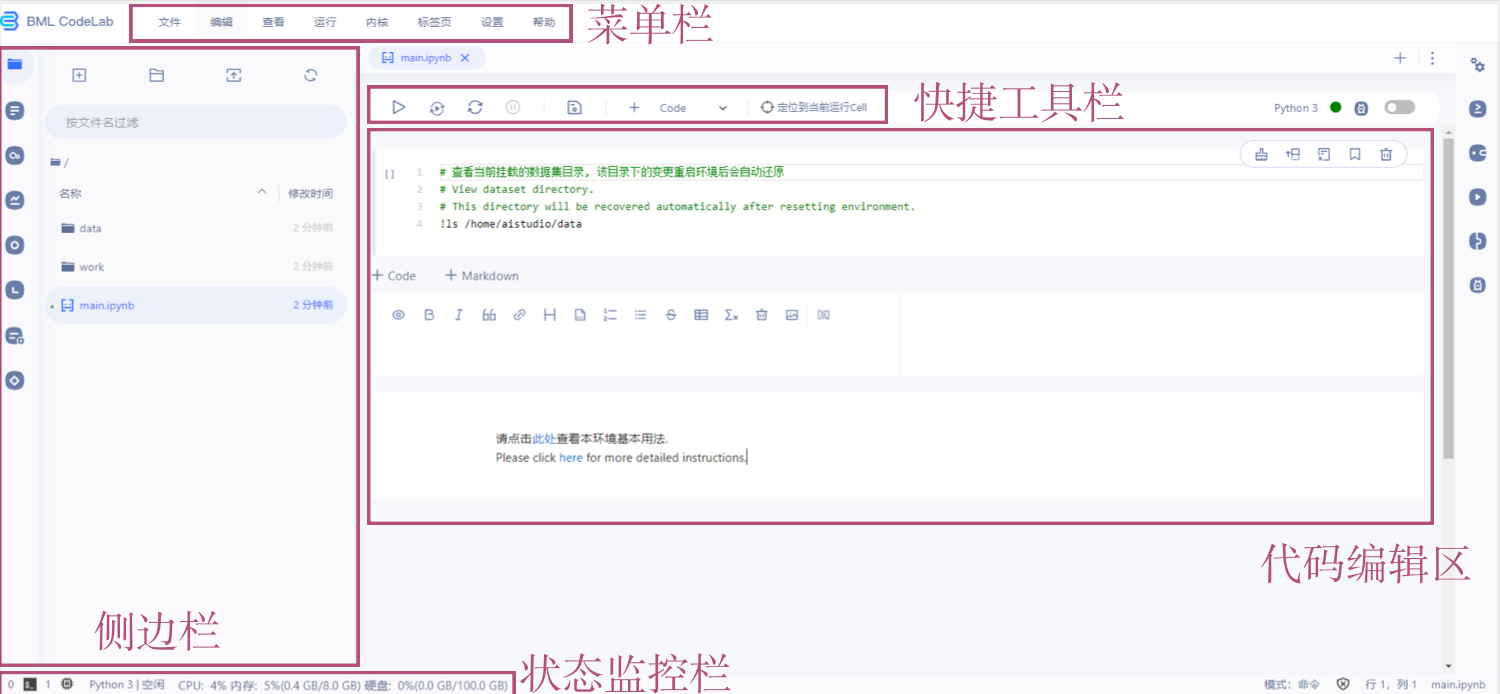
代码编辑区主要由代码编写单元(Code Cell)组成，在代码编写单元内编写Python代码或shell命令，点击“运行”按钮，代码或命令将在云端执行，并将结果返回到代码编写单元，直接显示在项目页面中。图1.3中我们简单定义两行代码，通过运行代码编写单元，得到输出结果。

图1.3 代码编写单元交互式运行

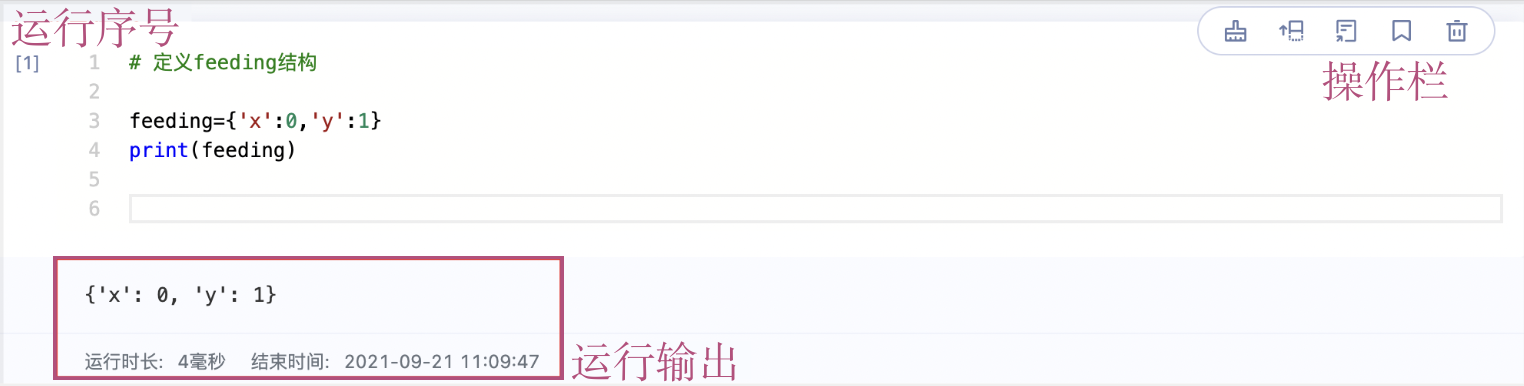
快捷工具栏内工具如图1.4所示，工具功能为：

运行：运行当前选中的代码编写单元。
停止运行：停止Notebook的运行状态。
重启内核：重启代码内核，清空环境中的环境变量、缓存变量、输出结果等.
保存：保存Notebook项目文件.
插入：添加指定类型的单元，支持Code和Markdown两种类型。
定位：定位到正在执行的单元。

图1.4 快捷工具栏

1.2 张量

在深度学习的实践中，我们通常使用向量或矩阵运算来提高计算效率。比如 $w_1x_1 + w_2 x_2 +\cdots +w_N x_N$ 的计算可以用$ w^\top x $来代替（其中$ w=[w_1 w_2 \cdots w_N]^\top， x=[x_1 x_2 \cdots x_N]^\top$），这样可以充分利用计算机的并行计算能力，特别是利用GPU来实现高效矩阵运算。

在深度学习框架中，数据经常用张量(Tensor)的形式来存储。张量是矩阵的扩展与延伸，可以认为是高阶的矩阵。1阶张量为向量，2阶张量为矩阵。如果你对Numpy熟悉，那么张量是类似于Numpy的多维数组(ndarray)的概念，可以具有任意多的维度。

笔记

注意：这里的“维度”是“阶”的概念，和线性代数中向量的“维度”含义不同。

张量的大小可以用形状（shape）来描述。比如一个三维张量的形状是 $[2, 2, 5]$ ，表示每一维（也称为轴（axis））的元素的数量，即第0轴上元素数量是2，第1轴上元素数量是2，第2轴上的元素数量为5。

图1.5给出了3种纬度的张量可视化表示。

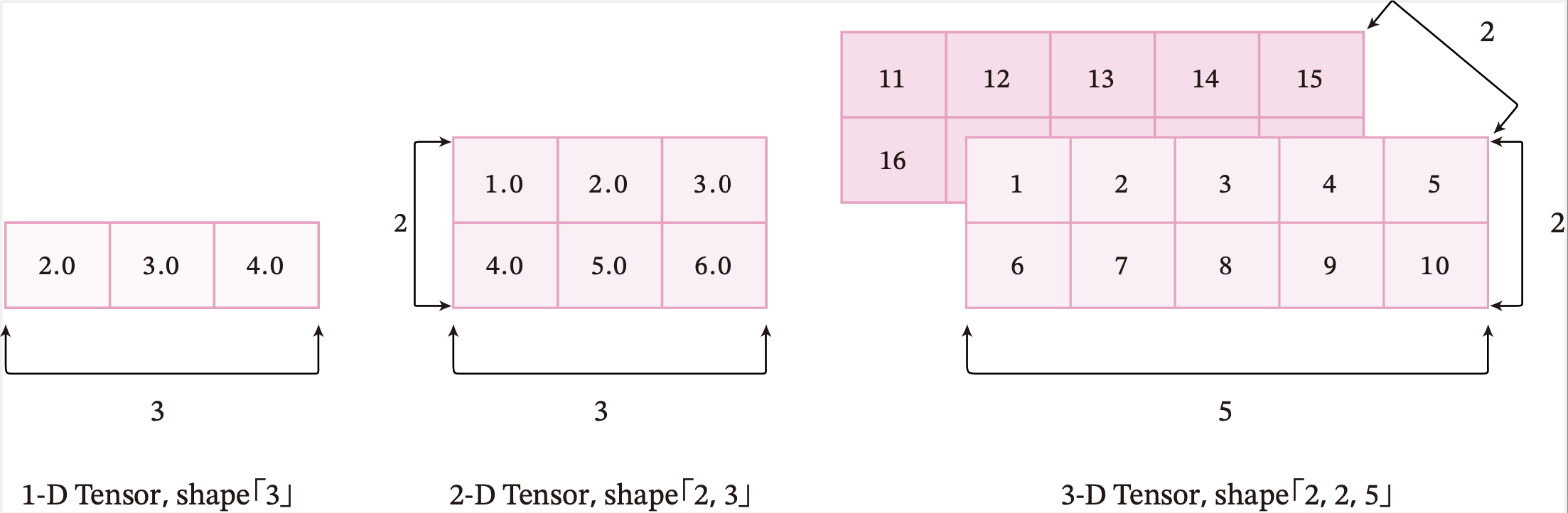
图1.5 不同维度的张量可视化表示

张量中元素的类型可以是布尔型数据、整数、浮点数或者复数，但同一张量中所有元素的数据类型均相同。因此我们可以给张量定义一个数据类型(dtype)来表示其元素的类型。

1.2.1 创建张量

创建一个张量可以有多种方式，如：指定数据创建、指定形状创建、指定区间创建等。

1.2.1.1 指定数据创建张量

通过给定Python列表数据，可以创建任意维度的张量。

（1）通过指定的Python列表数据[2.0, 3.0, 4.0]，创建一个一维张量。

# 导入PaddlePaddle
import paddle
# 创建一维Tensor
ndim_1_Tensor = paddle.to_tensor([2.0, 3.0, 4.0])
print(ndim_1_Tensor)

Tensor(shape=[3], dtype=float32, place=CPUPlace, stop_gradient=True,[2., 3., 4.])

（2）通过指定的Python列表数据来创建类似矩阵（matrix）的二维张量。

# 创建二维Tensor
ndim_2_Tensor = paddle.to_tensor([[1.0, 2.0, 3.0],[4.0, 5.0, 6.0]])
print(ndim_2_Tensor)

Tensor(shape=[2, 3], dtype=float32, place=CPUPlace, stop_gradient=True,[[1., 2., 3.],[4., 5., 6.]])

（3）同样地，还可以创建维度为3、4…N等更复杂的多维张量。

# 创建多维Tensor
ndim_3_Tensor = paddle.to_tensor([[[1, 2, 3, 4, 5],[6, 7, 8, 9, 10]],[[11, 12, 13, 14, 15],[16, 17, 18, 19, 20]]])
print(ndim_3_Tensor)

Tensor(shape=[2, 2, 5], dtype=int64, place=CPUPlace, stop_gradient=True,[[[1 , 2 , 3 , 4 , 5 ],[6 , 7 , 8 , 9 , 10]],[[11, 12, 13, 14, 15],[16, 17, 18, 19, 20]]])

需要注意的是，张量在任何一个维度上的元素数量必须相等。下面尝试定义一个在同一维度上元素数量不等的张量。

# 尝试定义在不同维度上元素数量不等的Tensor
ndim_2_Tensor = paddle.to_tensor([[1.0, 2.0],[4.0, 5.0, 6.0]])

输出结果为：

ValueError:Faild to convert input data to a regular ndarray :- Usually this means the input data contains nested lists with different lengths.

从输出结果看，这种定义情况会抛出异常，提示在任何维度上的元素数量必须相等。

1.2.1.2 指定形状创建

如果要创建一个指定形状、元素数据相同的张量，可以使用paddle.zeros、paddle.ones、paddle.full等API。

m, n = 2, 3# 使用paddle.zeros创建数据全为0，形状为[m, n]的Tensor
zeros_Tensor = paddle.zeros([m, n])# 使用paddle.ones创建数据全为1，形状为[m, n]的Tensor
ones_Tensor = paddle.ones([m, n])# 使用paddle.full创建数据全为指定值，形状为[m, n]的Tensor，这里我们指定数据为10
full_Tensor = paddle.full([m, n], 10)print('zeros Tensor: ', zeros_Tensor)
print('ones Tensor: ', ones_Tensor)
print('full Tensor: ', full_Tensor)

zeros Tensor:  Tensor(shape=[2, 3], dtype=float32, place=CPUPlace, stop_gradient=True,[[0., 0., 0.],[0., 0., 0.]])
ones Tensor:  Tensor(shape=[2, 3], dtype=float32, place=CPUPlace, stop_gradient=True,[[1., 1., 1.],[1., 1., 1.]])
full Tensor:  Tensor(shape=[2, 3], dtype=float32, place=CPUPlace, stop_gradient=True,[[10., 10., 10.],[10., 10., 10.]])

1.2.1.3 指定区间创建

如果要在指定区间内创建张量，可以使用paddle.arange、paddle.linspace等API。

# 使用paddle.arange创建以步长step均匀分隔数值区间[start, end)的一维Tensor
arange_Tensor = paddle.arange(start=1, end=5, step=1)# 使用paddle.linspace创建以元素个数num均匀分隔数值区间[start, stop]的Tensor
# [start, stop]为双闭区间，在该区间内创造5个元素的等差数列。而paddle.logspace是创造等比数列
linspace_Tensor = paddle.linspace(start=1, stop=5, num=5)print('arange Tensor: ', arange_Tensor)
print('linspace Tensor: ', linspace_Tensor)

arange Tensor:  Tensor(shape=[4], dtype=int64, place=CPUPlace, stop_gradient=True,[1, 2, 3, 4])
linspace Tensor:  Tensor(shape=[5], dtype=float32, place=CPUPlace, stop_gradient=True,[1., 2., 3., 4., 5.])

1.2.2 张量的属性

1.2.2.1 张量的形状

张量具有如下形状属性：

Tensor.ndim：张量的维度，例如向量的维度为1，矩阵的维度为2。
Tensor.shape：张量每个维度上元素的数量。
Tensor.shape[n]：张量第 $n$ 维的大小。第 $n$ 维也称为轴（axis）。
Tensor.size：张量中全部元素的个数。

为了更好地理解ndim、shape、axis、size四种属性间的区别，创建一个如图1.6所示的四维张量。

图1.6 形状为[2, 3, 4, 5]的四维张量

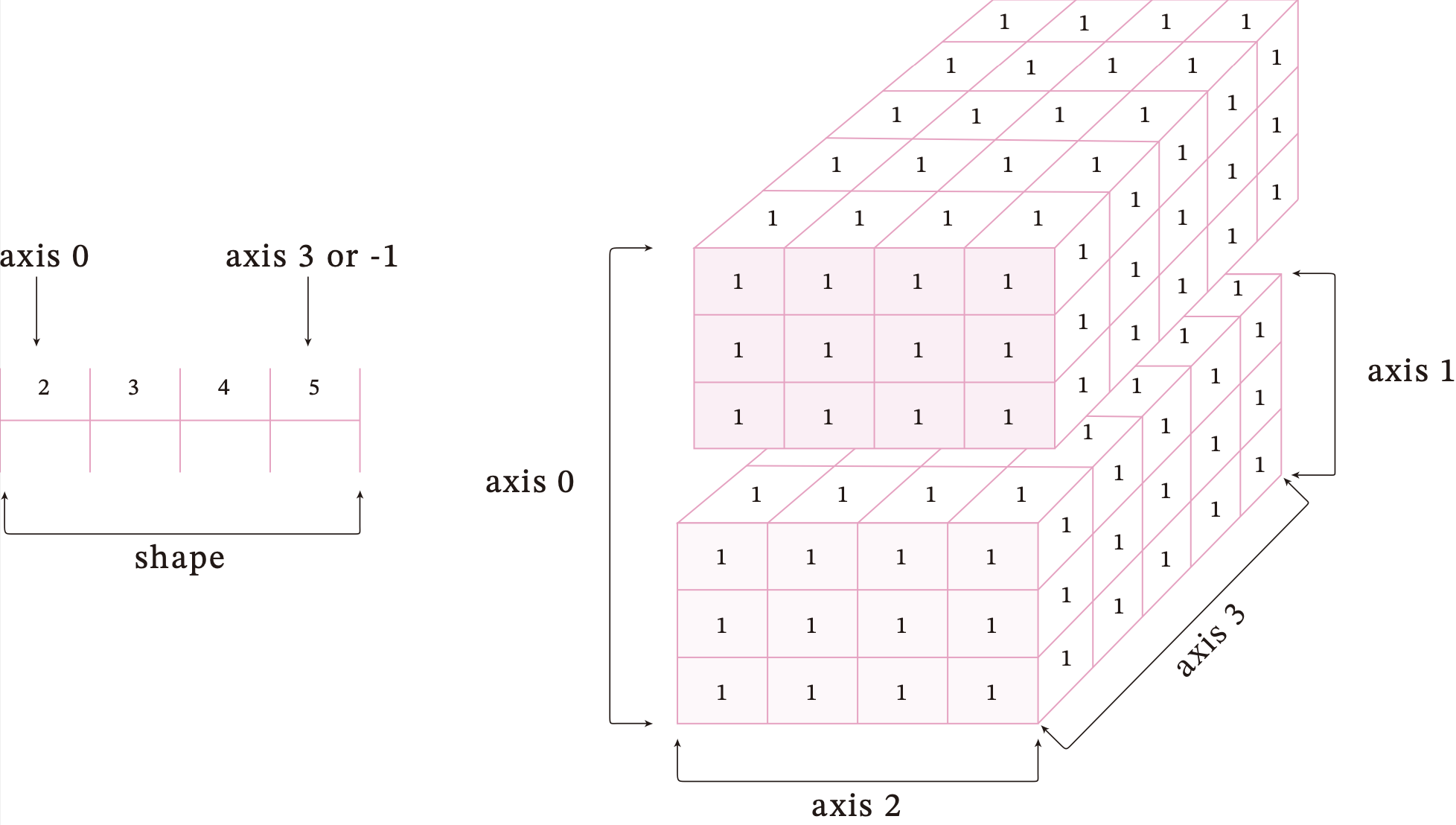
创建一个四维张量，并打印出shape、ndim、shape[n]、size属性。

ndim_4_Tensor = paddle.ones([2, 3, 4, 5])print("Number of dimensions:", ndim_4_Tensor.ndim)
print("Shape of Tensor:", ndim_4_Tensor.shape)
print("张量0轴上的元素数:", ndim_4_Tensor.shape[0])
print("张量最后一个轴上的元素数:", ndim_4_Tensor.shape[-1])
print('Number of elements in Tensor: ', ndim_4_Tensor.size)

Number of dimensions: 4
Shape of Tensor: [2, 3, 4, 5]
张量0轴上的元素数: 2
张量最后一个轴上的元素数: 5
Number of elements in Tensor:  120

1.2.2.2 形状的改变

除了查看张量的形状外，重新设置张量的在实际编程中也具有重要意义，飞桨提供了paddle.reshape接口来改变张量的形状。

# 定义一个shape为[3,2,5]的三维Tensor
ndim_3_Tensor = paddle.to_tensor([[[1, 2, 3, 4, 5],[6, 7, 8, 9, 10]],[[11, 12, 13, 14, 15],[16, 17, 18, 19, 20]],[[21, 22, 23, 24, 25],[26, 27, 28, 29, 30]]])
print("the shape of ndim_3_Tensor:", ndim_3_Tensor.shape)# paddle.reshape 可以保持在输入数据不变的情况下，改变数据形状。这里我们设置reshape为[2,5,3]
reshape_Tensor = paddle.reshape(ndim_3_Tensor, [2, 5, 3])
print("After reshape:", reshape_Tensor)

the shape of ndim_3_Tensor: [3, 2, 5]
After reshape: Tensor(shape=[2, 5, 3], dtype=int64, place=CPUPlace, stop_gradient=True,[[[1 , 2 , 3 ],[4 , 5 , 6 ],[7 , 8 , 9 ],[10, 11, 12],[13, 14, 15]],[[16, 17, 18],[19, 20, 21],[22, 23, 24],[25, 26, 27],[28, 29, 30]]])

从输出结果看，将张量从[3, 2, 5]的形状reshape为[2, 5, 3]的形状时，张量内的数据不会发生改变，元素顺序也没有发生改变，只有数据形状发生了改变。

笔记

使用reshape时存在一些技巧，比如：

-1表示这个维度的值是从张量的元素总数和剩余维度推断出来的。因此，有且只有一个维度可以被设置为-1。
0表示实际的维数是从张量的对应维数中复制出来的，因此shape中0所对应的索引值不能超过张量的总维度。

分别对上文定义的ndim_3_Tensor进行reshape为[-1]和reshape为[0, 5, 2]两种操作，观察新张量的形状。

new_Tensor1 = ndim_3_Tensor.reshape([-1])
print('new Tensor 1 shape: ', new_Tensor1.shape)
new_Tensor2 = ndim_3_Tensor.reshape([0, 5, 2])
print('new Tensor 2 shape: ', new_Tensor2.shape)

new Tensor 1 shape:  [30]
new Tensor 2 shape:  [3, 5, 2]

从输出结果看，第一行代码中的第一个reshape操作将张量reshape为元素数量为30的一维向量；第四行代码中的第二个reshape操作中，0对应的维度的元素个数与原张量在该维度上的元素个数相同。

除使用paddle.reshape进行张量形状的改变外，还可以通过paddle.unsqueeze将张量中的一个或多个维度中插入尺寸为1的维度。

ones_Tensor = paddle.ones([5, 10])
new_Tensor1 = paddle.unsqueeze(ones_Tensor, axis=0)
print('new Tensor 1 shape: ', new_Tensor1.shape)
new_Tensor2 = paddle.unsqueeze(ones_Tensor, axis=[1, 2])
print('new Tensor 2 shape: ', new_Tensor2.shape)

new Tensor 1 shape:  [1, 5, 10]
new Tensor 2 shape:  [5, 1, 1, 10]

1.2.2.3 张量的数据类型

飞桨中可以通过Tensor.dtype来查看张量的数据类型，类型支持bool、float16、float32、float64、uint8、int8、int16、int32、int64和复数类型数据。

1）通过Python元素创建的张量，可以通过dtype来指定数据类型，如果未指定：

对于Python整型数据，则会创建int64型张量。
对于Python浮点型数据，默认会创建float32型张量。

2）通过Numpy数组创建的张量，则与其原来的数据类型保持相同。通过paddle.to_tensor()函数可以将Numpy数组转化为张量。

# 使用paddle.to_tensor通过已知数据来创建一个Tensor
print("来自Python整数的张量dtype:", paddle.to_tensor(1).dtype)
print("来自Python浮点的张量dtype:", paddle.to_tensor(1.0).dtype)

来自Python整数的张量dtype: paddle.int64
来自Python浮点的张量dtype: paddle.float32

如果想改变张量的数据类型，可以通过调用paddle.castAPI来实现。

# 定义dtype为float32的Tensor
float32_Tensor = paddle.to_tensor(1.0)
# paddle.cast可以将输入数据的数据类型转换为指定的dtype并输出。支持输出和输入数据类型相同。
int64_Tensor = paddle.cast(float32_Tensor, dtype='int64')
print("转换为int64后的张量:", int64_Tensor.dtype)

转换为int64后的张量: paddle.int64

1.2.2.4 张量的设备位置

初始化张量时可以通过place来指定其分配的设备位置，可支持的设备位置有三种：CPU、GPU和固定内存。

固定内存也称为不可分页内存或锁页内存，它与GPU之间具有更高的读写效率，并且支持异步传输，这对网络整体性能会有进一步提升，但它的缺点是分配空间过多时可能会降低主机系统的性能，因为它减少了用于存储虚拟内存数据的可分页内存。当未指定设备位置时，张量默认设备位置和安装的飞桨版本一致，如安装了GPU版本的飞桨，则设备位置默认为GPU。

如下代码分别创建了CPU、GPU和固定内存上的张量，并通过Tensor.place查看张量所在的设备位置。

# 创建CPU上的Tensor
cpu_Tensor = paddle.to_tensor(1, place=paddle.CPUPlace())
# 通过Tensor.place查看张量所在设备位置
print('cpu Tensor: ', cpu_Tensor.place)# 创建GPU上的Tensor
gpu_Tensor = paddle.to_tensor(1, place=paddle.CUDAPlace(0))
print('gpu Tensor: ', gpu_Tensor.place)# 创建固定内存上的Tensor
pin_memory_Tensor = paddle.to_tensor(1, place=paddle.CUDAPinnedPlace())
print('pin memory Tensor: ', pin_memory_Tensor.place)

cpu Tensor:  CPUPlace
gpu Tensor:  CUDAPlace(0)
pin memory Tensor:  CUDAPinnedPlace

1.2.3 张量与Numpy数组转换

张量和Numpy数组可以相互转换。第1.2.2.3节中我们了解到paddle.to_tensor()函数可以将Numpy数组转化为张量，也可以通过Tensor.numpy()函数将张量转化为Numpy数组。

ndim_1_Tensor = paddle.to_tensor([1., 2.])
# 将当前 Tensor 转化为 numpy.ndarray
print('Tensor to convert: ', ndim_1_Tensor.numpy())

Tensor to convert:  [1. 2.]

1.2.4 张量的访问

1.2.4.1 索引和切片

我们可以通过索引或切片方便地访问或修改张量。飞桨使用标准的Python索引规则与Numpy索引规则，具有以下特点：

基于 $0 - n$ 的下标进行索引，如果下标为负数，则从尾部开始计算。
通过冒号“:”分隔切片参数start:stop:step来进行切片操作，也就是访问start到stop范围内的部分元素并生成一个新的序列。其中start为切片的起始位置，stop为切片的截止位置，step是切片的步长，这三个参数均可缺省。

1.2.4.2 访问张量

针对一维张量，对单个轴进行索引和切片。

# 定义1个一维Tensor
ndim_1_Tensor = paddle.to_tensor([0, 1, 2, 3, 4, 5, 6, 7, 8])print("初始张量:", ndim_1_Tensor)
print("First element:", ndim_1_Tensor[0])
print("Last element:", ndim_1_Tensor[-1])
print("All element:", ndim_1_Tensor[:])
print("前3个元素:", ndim_1_Tensor[:3])
print("间隔3个元素:", ndim_1_Tensor[::3])
print("张量翻转:", ndim_1_Tensor[::-1])

初始张量: Tensor(shape=[9], dtype=int64, place=CUDAPlace(0), stop_gradient=True,[0, 1, 2, 3, 4, 5, 6, 7, 8])
First element: Tensor(shape=[1], dtype=int64, place=CUDAPlace(0), stop_gradient=True,[0])
Last element: Tensor(shape=[1], dtype=int64, place=CUDAPlace(0), stop_gradient=True,[8])
All element: Tensor(shape=[9], dtype=int64, place=CUDAPlace(0), stop_gradient=True,[0, 1, 2, 3, 4, 5, 6, 7, 8])
前3个元素: Tensor(shape=[3], dtype=int64, place=CUDAPlace(0), stop_gradient=True,[0, 1, 2])
间隔3个元素: Tensor(shape=[3], dtype=int64, place=CUDAPlace(0), stop_gradient=True,[0, 3, 6])
张量翻转: Tensor(shape=[9], dtype=int64, place=CUDAPlace(0), stop_gradient=True,[8, 7, 6, 5, 4, 3, 2, 1, 0])

针对二维及以上维度的张量，在多个维度上进行索引或切片。索引或切片的第一个值对应第0维，第二个值对应第1维，以此类推，如果某个维度上未指定索引，则默认为“:”。

# 定义1个二维Tensor
ndim_2_Tensor = paddle.to_tensor([[0, 1, 2, 3],[4, 5, 6, 7],[8, 9, 10, 11]])
print("初始张量:", ndim_2_Tensor)
print("First row:", ndim_2_Tensor[0])
print("First row:", ndim_2_Tensor[0, :])
print("First column:", ndim_2_Tensor[:, 0])
print("Last column:", ndim_2_Tensor[:, -1])
print("All element:", ndim_2_Tensor[:])
print("First row and second column:", ndim_2_Tensor[0, 1])

初始张量: Tensor(shape=[3, 4], dtype=int64, place=CUDAPlace(0), stop_gradient=True,[[0 , 1 , 2 , 3 ],[4 , 5 , 6 , 7 ],[8 , 9 , 10, 11]])
First row: Tensor(shape=[4], dtype=int64, place=CUDAPlace(0), stop_gradient=True,[0, 1, 2, 3])
First row: Tensor(shape=[4], dtype=int64, place=CUDAPlace(0), stop_gradient=True,[0, 1, 2, 3])
First column: Tensor(shape=[3], dtype=int64, place=CUDAPlace(0), stop_gradient=True,[0, 4, 8])
Last column: Tensor(shape=[3], dtype=int64, place=CUDAPlace(0), stop_gradient=True,[3 , 7 , 11])
All element: Tensor(shape=[3, 4], dtype=int64, place=CUDAPlace(0), stop_gradient=True,[[0 , 1 , 2 , 3 ],[4 , 5 , 6 , 7 ],[8 , 9 , 10, 11]])
First row and second column: Tensor(shape=[1], dtype=int64, place=CUDAPlace(0), stop_gradient=True,[1])

1.2.4.3 修改张量

与访问张量类似，可以在单个或多个轴上通过索引或切片操作来修改张量。

提醒
慎重通过索引或切片操作来修改张量，此操作仅会原地修改该张量的数值，且原值不会被保存。如果被修改的张量参与梯度计算，将仅会使用修改后的数值，这可能会给梯度计算引入风险。

# 定义1个二维Tensor
ndim_2_Tensor = paddle.ones([2, 3], dtype='float32')
print('初始张量: ', ndim_2_Tensor)# 修改第1维为0
ndim_2_Tensor[0] = 0
print('修改后的张量: ', ndim_2_Tensor)# 修改第1维为2.1
ndim_2_Tensor[0:1] = 2.1
print('修改后的张量: ', ndim_2_Tensor)# 修改全部Tensor
ndim_2_Tensor[...] = 3
print('修改后的张量: ', ndim_2_Tensor)

初始张量:  Tensor(shape=[2, 3], dtype=float32, place=CUDAPlace(0), stop_gradient=True,[[1., 1., 1.],[1., 1., 1.]])
修改后的张量:  Tensor(shape=[2, 3], dtype=float32, place=CUDAPlace(0), stop_gradient=True,[[0., 0., 0.],[1., 1., 1.]])
修改后的张量:  Tensor(shape=[2, 3], dtype=float32, place=CUDAPlace(0), stop_gradient=True,[[2.09999990, 2.09999990, 2.09999990],[1.        , 1.        , 1.        ]])
修改后的张量:  Tensor(shape=[2, 3], dtype=float32, place=CUDAPlace(0), stop_gradient=True,[[3., 3., 3.],[3., 3., 3.]])

1.2.5 张量的运算

张量支持包括基础数学运算、逻辑运算、矩阵运算等100余种运算操作，以加法为例，有如下两种实现方式：
1）使用飞桨API paddle.add(x,y)。
2）使用张量类成员函数x.add(y)。

# 定义两个Tensor
x = paddle.to_tensor([[1.1, 2.2], [3.3, 4.4]], dtype="float64")
y = paddle.to_tensor([[5.5, 6.6], [7.7, 8.8]], dtype="float64")
# 第一种调用方法，paddle.add逐元素相加算子，并将各个位置的输出元素保存到返回结果中
print('Method 1: ', paddle.add(x, y))
# 第二种调用方法
print('Method 2: ', x.add(y))

Method 1:  Tensor(shape=[2, 2], dtype=float64, place=CUDAPlace(0), stop_gradient=True,[[6.60000000 , 8.80000000 ],[11.        , 13.20000000]])
Method 2:  Tensor(shape=[2, 2], dtype=float64, place=CUDAPlace(0), stop_gradient=True,[[6.60000000 , 8.80000000 ],[11.        , 13.20000000]])

从输出结果看，使用张量类成员函数和飞桨API具有相同的效果。

笔记
由于张量类成员函数操作更为方便，以下均从张量类成员函数的角度，对常用张量操作进行介绍。

笔记
更多张量操作相关的API，请参考飞桨官方文档。

1.2.5.1 数学运算

张量类的基础数学函数如下：

x.abs()                       # 逐元素取绝对值
x.ceil()                      # 逐元素向上取整
x.floor()                     # 逐元素向下取整
x.round()                     # 逐元素四舍五入
x.exp()                       # 逐元素计算自然常数为底的指数
x.log()                       # 逐元素计算x的自然对数
x.reciprocal()                # 逐元素求倒数
x.square()                    # 逐元素计算平方
x.sqrt()                      # 逐元素计算平方根
x.sin()                       # 逐元素计算正弦
x.cos()                       # 逐元素计算余弦
x.add(y)                      # 逐元素加
x.subtract(y)                 # 逐元素减
x.multiply(y)                 # 逐元素乘（积）
x.divide(y)                   # 逐元素除
x.mod(y)                      # 逐元素除并取余
x.pow(y)                      # 逐元素幂
x.max()                       # 指定维度上元素最大值，默认为全部维度
x.min()                       # 指定维度上元素最小值，默认为全部维度
x.prod()                      # 指定维度上元素累乘，默认为全部维度
x.sum()                       # 指定维度上元素的和，默认为全部维度

同时，为了更方便地使用张量，飞桨对Python数学运算相关的魔法函数进行了重写，以下操作与上述结果相同。

x + y  -> x.add(y)            # 逐元素加
x - y  -> x.subtract(y)       # 逐元素减
x * y  -> x.multiply(y)       # 逐元素乘（积）
x / y  -> x.divide(y)         # 逐元素除
x % y  -> x.mod(y)            # 逐元素除并取余
x ** y -> x.pow(y)            # 逐元素幂

1.2.5.2 逻辑运算

张量类的逻辑运算函数如下：

x.isfinite()                  # 判断Tensor中元素是否是有限的数字，即不包括inf与nan
x.equal_all(y)                # 判断两个Tensor的全部元素是否相等，并返回形状为[1]的布尔类Tensor
x.equal(y)                    # 判断两个Tensor的每个元素是否相等，并返回形状相同的布尔类Tensor
x.not_equal(y)                # 判断两个Tensor的每个元素是否不相等
x.less_than(y)                # 判断Tensor x的元素是否小于Tensor y的对应元素
x.less_equal(y)               # 判断Tensor x的元素是否小于或等于Tensor y的对应元素
x.greater_than(y)             # 判断Tensor x的元素是否大于Tensor y的对应元素
x.greater_equal(y)            # 判断Tensor x的元素是否大于或等于Tensor y的对应元素
x.allclose(y)                 # 判断两个Tensor的全部元素是否接近

同样地，飞桨对Python逻辑比较相关的魔法函数也进行了重写，这里不再赘述。

1.2.5.3 矩阵运算

张量类还包含了矩阵运算相关的函数，如矩阵的转置、范数计算和乘法等。

x.t()                         # 矩阵转置
x.transpose([1, 0])           # 交换第 0 维与第 1 维的顺序
x.norm('fro')                 # 矩阵的弗罗贝尼乌斯范数
x.dist(y, p=2)                # 矩阵（x-y）的2范数
x.matmul(y)                   # 矩阵乘法

有些矩阵运算中也支持大于两维的张量，比如matmul函数，对最后两个维度进行矩阵乘。比如x是形状为[j,k,n,m]的张量，另一个y是[j,k,m,p]的张量，则x.matmul(y)输出的张量形状为[j,k,n,p]。

1.2.5.4 广播机制

飞桨的一些API在计算时支持广播(Broadcasting)机制，允许在一些运算时使用不同形状的张量。通常来讲，如果有一个形状较小和一个形状较大的张量，会希望多次使用较小的张量来对较大的张量执行某些操作，看起来像是形状较小的张量首先被扩展到和较大的张量形状一致，然后再做运算。

广播机制的条件

飞桨的广播机制主要遵循如下规则（参考Numpy广播机制）：

1）每个张量至少为一维张量。

2）从后往前比较张量的形状，当前维度的大小要么相等，要么其中一个等于1，要么其中一个不存在。

# 当两个Tensor的形状一致时，可以广播
x = paddle.ones((2, 3, 4))
y = paddle.ones((2, 3, 4))
z = x + y
print('用两个形状相同的张量进行广播: ', z.shape)x = paddle.ones((2, 3, 1, 5))
y = paddle.ones((3, 4, 1))
# 从后往前依次比较：
# 第一次：y的维度大小是1
# 第二次：x的维度大小是1
# 第三次：x和y的维度大小相等，都为3
# 第四次：y的维度不存在
# 所以x和y是可以广播的
z = x + y
print('用两个形状不相同的张量进行广播:', z.shape)

用两个形状相同的张量进行广播:  [2, 3, 4]
用两个形状不相同的张量进行广播: [2, 3, 4, 5]

从输出结果看，x与y在上述两种情况中均遵循广播规则，因此在张量相加时可以广播。我们再定义两个shape分别为[2, 3, 4]和[2, 3, 6]的张量，观察这两个张量是否能够通过广播操作相加。

x = paddle.ones((2, 3, 4))
y = paddle.ones((2, 3, 6))
z = x + y

输出结果为：

ValueError: (InvalidArgument) Broadcast dimension mismatch.

从输出结果看，此时x和y是不能广播的，因为在第一次从后往前的比较中，4和6不相等，不符合广播规则。

广播机制的计算规则

现在我们知道在什么情况下两个张量是可以广播的。两个张量进行广播后的结果张量的形状计算规则如下：

1）如果两个张量shape的长度不一致，那么需要在较小长度的shape前添加1，直到两个张量的形状长度相等。

2）保证两个张量形状相等之后，每个维度上的结果维度就是当前维度上较大的那个。

以张量x和y进行广播为例，x的shape为[2, 3, 1，5]，张量y的shape为[3，4，1]。首先张量y的形状长度较小，因此要将该张量形状补齐为[1, 3, 4, 1]，再对两个张量的每一维进行比较。从第一维看，x在一维上的大小为2，y为1，因此，结果张量在第一维的大小为2。以此类推，对每一维进行比较，得到结果张量的形状为[2, 3, 4, 5]。

由于矩阵乘法函数paddle.matmul在深度学习中使用非常多，这里需要特别说明一下它的广播规则：

1）如果两个张量均为一维，则获得点积结果。

2）如果两个张量都是二维的，则获得矩阵与矩阵的乘积。

3）如果张量x是一维，y是二维，则将x的shape转换为[1, D]，与y进行矩阵相乘后再删除前置尺寸。

4）如果张量x是二维，y是一维，则获得矩阵与向量的乘积。

5）如果两个张量都是N维张量（N > 2），则根据广播规则广播非矩阵维度（除最后两个维度外其余维度）。比如：如果输入x是形状为[j,1,n,m]的张量，另一个y是[k,m,p]的张量，则输出张量的形状为[j,k,n,p]。

x = paddle.ones([10, 1, 5, 2])
y = paddle.ones([3, 2, 5])
z = paddle.matmul(x, y)
print('After matmul: ', z.shape)

After matmul:  [10, 3, 5, 5]

从输出结果看，计算张量乘积时会使用到广播机制。

笔记
飞桨的API有原位（inplace）操作和非原位操作之分。原位操作即在原张量上保存操作结果，非原位操作则不会修改原张量，而是返回一个新的张量来表示运算结果。在飞桨框架V2.1及之后版本，部分API有对应的原位操作版本，在API后加上’_'表示，如：x.add(y)是非原位操作，x.add_(y)为原位操作。

动手练习1.2
尝试和熟悉本节中的各种张量运算，特别是掌握张量计算时的广播机制。

1.3 算子

一个复杂的机器学习模型（比如神经网络）可以看作一个复合函数，输入是数据特征，输出是标签的值或概率。简单起见，假设一个由 $L$ 个函数复合的神经网络定义为：
$y=f_L(\cdots f_2(f_1(x))),$

其中 $f_l(\cdot)$ 可以为带参数的函数，也可以为不带参数的函数， $x$ 为输入特征， $y$ 为某种损失。
我们将从 $x$ 到 $y$ 的计算看作一个前向计算过程。而神经网络的参数学习需要计算损失关于所有参数的偏导数（即梯度）。假设函数 $f_l(\cdot)$ 包含参数 $\theta_l$ ，根据链式法则，

$\begin{aligned} \frac{\partial y}{\partial \theta_l} &= {\frac{\partial f_l}{\partial \theta_l}} \frac{\partial y}{\partial f_l} \\ &= \frac{\partial f_l}{\partial \theta_l} \frac{\partial f_{l+1}}{\partial f_l} \cdots \frac{\partial f_L}{\partial f_{L-1}} . \end{aligned}$

在实践中，一种比较高效的计算 $y$ 关于每个函数 $f_l$ 的偏导数的方式是利用递归进行反向计算。令 $\delta_l\triangleq \frac{\partial y}{\partial f_l}$ ，则有
$\delta_{l-1} = \frac{\partial f_l}{\partial f_{l-1}} \delta_{l}.$

如果将函数 $f_l(\cdot)$ 称为前向函数，则 $\delta_{l-1}$ 的计算称为函数 $f (x)$ 的反向函数。

如果我们实现每个基础函数的前向函数和反向函数，就可以非常方便地通过这些基础函数组合出复杂函数，并通过链式法则反向计算复杂函数的偏导数。
在深度学习框架中，这些基本函数的实现称为算子(Operator，Op)。有了算子，就可以像搭积木一样构建复杂的模型。

1.3.1 算子定义

算子是构建复杂机器学习模型的基础组件，包含一个函数 $f (x)$ 的前向函数和反向函数。为了可以更便捷地进行算子组合，本书中定义算子Op}的接口如下：

class Op(object):def __init__(self):passdef __call__(self, inputs):return self.forward(inputs)# 前向函数# 输入：张量inputs# 输出：张量outputsdef forward(self, inputs):# return outputsraise NotImplementedError# 反向函数# 输入：最终输出对outputs的梯度outputs_grads# 输出：最终输出对inputs的梯度inputs_gradsdef backward(self, outputs_grads):# return inputs_gradsraise NotImplementedError

在上面的接口中，forward是自定义Op的前向函数，必须被子类重写，它的参数为输入对象，参数的类型和数量任意；backward是自定义Op的反向函数，必须被子类重写，它的参数为forward输出张量的梯度outputs_grads，它的输出为forward输入张量的梯度inputs_grads。

笔记
在飞桨中，可以直接调用模型的forward()方法进行前向执行，也可以调用__call__，从而执行在forward()中定义的前向计算逻辑。

下面以 $\exp(a \times b+c \times d)$ 为例，分别实现加法、乘法和指数运算三个算子，通过算子组合计算 $y$ 值。

1.3.1.1 加法算子

图1.7展示了加法算子的前反向计算过程。

图1.7 加法算子的前反向函数

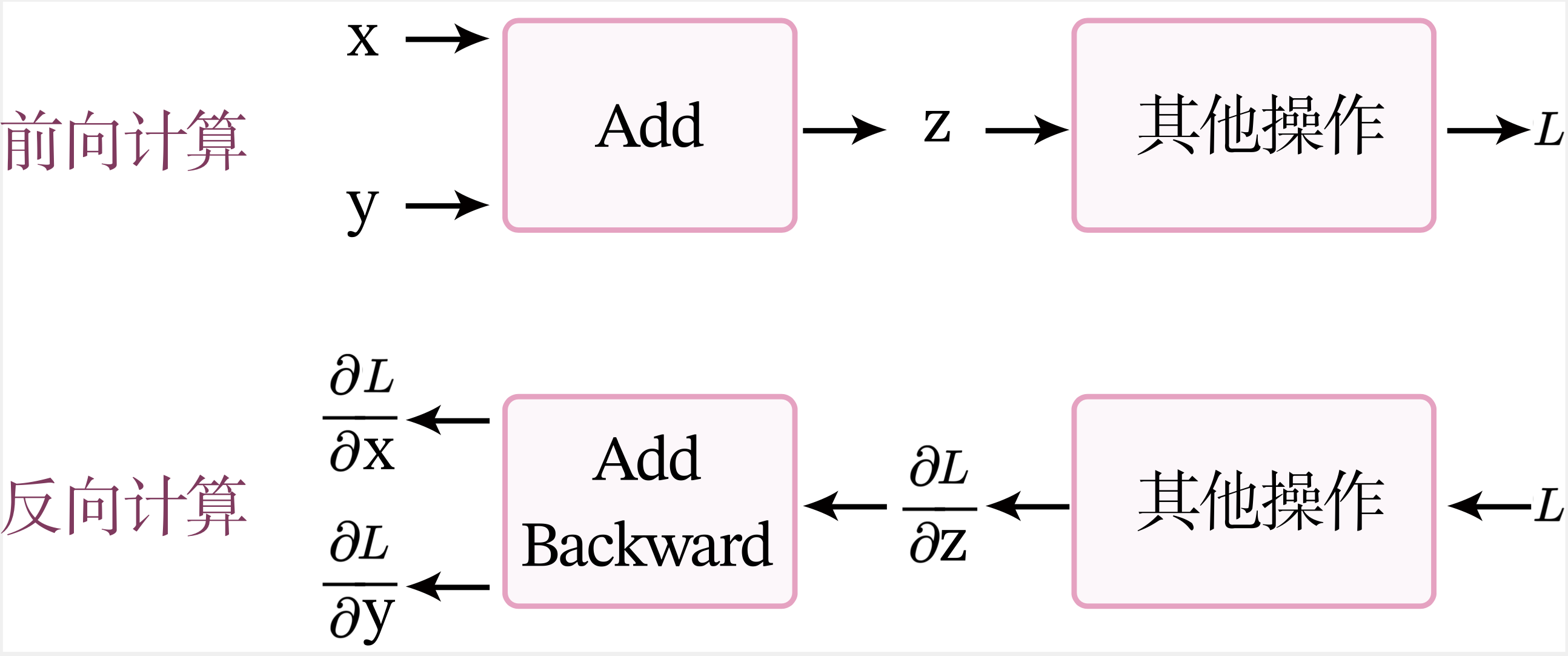
前向计算

当进行前向计算时，加法计算输出 $z = x + y$ 。

反向计算

假设经过一个其他操作后，最终输出为 $L$ ，令 $\delta_z=\frac{\partial L}{\partial z}$ ， $\delta_x=\frac{\partial L}{\partial x}$ ， $\delta_y=\frac{\partial L}{\partial y}$ 。
加法算子的反向计算的输入是梯度 $\delta_z$ ，输出是梯度 $\delta_x$ 和 $\delta_y$ 。

根据链式法则， $\delta_x = \delta_z \times 1$ ， $\delta_y = \delta_z \times 1$ 。
加法算子的代码实现如下：

class add(Op):def __init__(self):super(add, self).__init__()def __call__(self, x, y):return self.forward(x, y)def forward(self, x, y):self.x = xself.y = youtputs = x + yreturn outputsdef backward(self, grads):grads_x = grads * 1grads_y = grads * 1return grads_x, grads_y

定义 $x = 1$ 、 $y = 4$ ，根据反向计算，得到 $x$ 、 $y$ 的梯度。

x = 1
y = 4
add_op = add()
z = add_op(x, y)
grads_x, grads_y = add_op.backward(grads=1)
print("x's grad is: ", grads_x)
print("y's grad is: ", grads_y)

x's grad is:  1
y's grad is:  1

1.3.1.2 乘法算子

同理，乘法算子的代码实现如下：

class multiply(Op):def __init__(self):super(multiply, self).__init__()def __call__(self, x, y):return self.forward(x, y)def forward(self, x, y):self.x = xself.y = youtputs = x * yreturn outputsdef backward(self, grads):grads_x = grads * self.ygrads_y = grads * self.xreturn grads_x, grads_y

1.3.1.3 指数算子

同理，指数算子的代码实现如下：

import mathclass exponential(Op):def __init__(self):super(exponential, self).__init__()def forward(self, x):self.x = xoutputs = math.exp(x)return outputsdef backward(self, grads):grads = grads * math.exp(self.x)return grads

分别指定 $a 、 b 、 c 、 d$ 的值，通过实例化算子，调用加法、乘法和指数运算算子，计算得到 $y$ 。

a, b, c, d = 2, 3, 2, 2
# 实例化算子
multiply_op = multiply()
add_op = add()
exp_op = exponential()
y = exp_op(add_op(multiply_op(a, b), multiply_op(c, d)))
print('y: ', y)

y:  22026.465794806718

动手练习1.3

执行上述算子的反向过程，并验证梯度是否正确。

1.3.2 自动微分机制

目前大部分深度学习平台都支持自动微分（Automatic Differentiation），即根据forward()函数来自动构建backward()函数。

笔记

自动微分的原理是将所有的数值计算都分解为基本的原子操作，并构建计算图{Computational Graph}。计算图上每个节点都是一个原子操作，保留前向和反向的计算结果，很方便通过链式法则来计算梯度。自动微分的详细介绍可以参考《神经网络与深度学习》第4.5节。

飞桨的自动微分是通过trace的方式，记录各种算子和张量的前向计算，并自动创建相应的反向函数和反向变量，来实现反向梯度的计算。

笔记

在飞桨中，可以通过paddle.grad()API或张量类成员函数x.grad来查看张量的梯度。

下面用一个比较简单的例子来了解整个过程。定义两个张量a和b，并用stop_gradient属性用来设置是否传递梯度。将a的stop_gradient属性设为False，会自动为a创建一个反向张量，将b的stop_gradient属性设为True，即不会为b创建反向张量。

# 定义张量a，stop_gradient=False代表进行梯度传导
a = paddle.to_tensor(2.0, stop_gradient=False)# 定义张量b，stop_gradient=True代表不进行梯度传导
b = paddle.to_tensor(5.0, stop_gradient=True)
c = a * b# 自动计算反向梯度
c.backward()
print("张量a的梯度为: {}".format(a.grad))
print("张量b的梯度为: {}".format(b.grad))
print("张量c的梯度为s: {}".format(c.grad))

张量a的梯度为: Tensor(shape=[1], dtype=float32, place=CPUPlace, stop_gradient=False,[5.])
张量b的梯度为: None
张量c的梯度为s: Tensor(shape=[1], dtype=float32, place=CPUPlace, stop_gradient=False,[1.])

下面我们解释下上面代码的执行逻辑。

1.3.2.1 前向执行

在上面代码中，第7行c.backward()被执行前，会为每个张量和算子创建相应的反向张量和反向函数。

当创建张量或执行算子的前向计算时，会自动创建反向张量或反向算子。这里以上面代码中乘法为例来进行说明。

当创建张量a时，由于其属性stop_gradient=False，因此会自动为a创建一个反向张量，也就是图1.8中的a_grad。由于a不依赖其它张量或算子，a_grad的grad_op为None。
当创建张量b时，由于其属性stop_gradient=True，因此不会为b创建一个反向张量。
执行乘法 $c=a\times b$ 时， $\times$ 是一个前向算子Mul，为其构建反向算子MulBackward。由于Mul的输入是a和b，输出是c，对应反向算子MulBackward的输入是张量c的反向张量c_grad，输出是a和b的反向张量。如果输入定义stop_gradient=True，反向张量即为None。在此例子中就是a_grad和None。
反向算子MulBackward中的grad_pending_ops用于在自动构建反向网络时，明确该反向算子的下一个可执行的反向算子。可以理解为在反向计算中，该算子衔接的下一个反向算子。
当c通过乘法算子Mul被创建后，c会创建一个反向张量c_grad，它的grad_op为该乘法算子的反向算子，即MulBackward。

由于此时还没有进行反向计算，因此这些反向张量和反向算子中的具体数值为空(data = None)。此时，上面代码对应的计算图状态如图1.8所示。

图1.8 调用backward()前的计算图状态

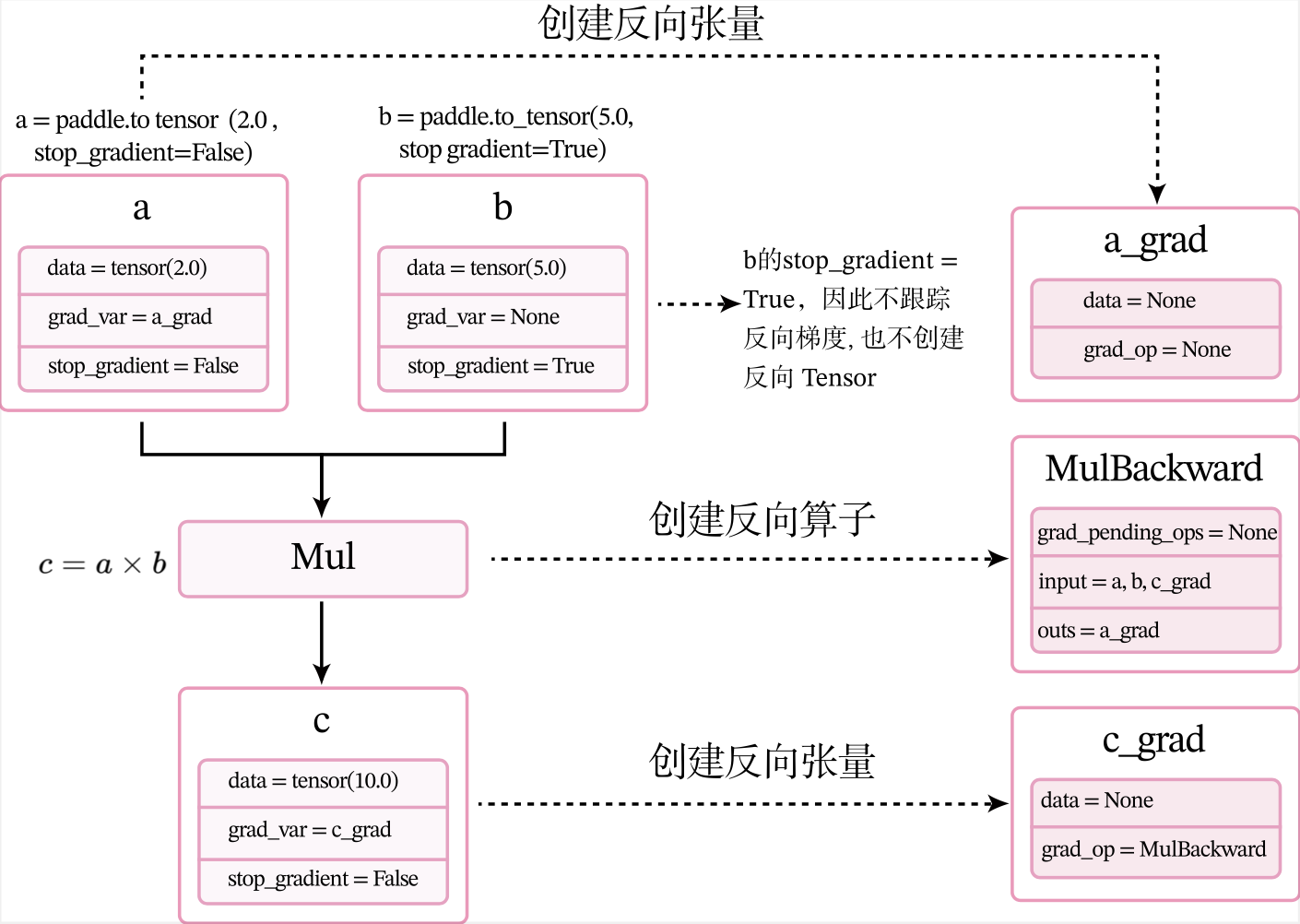
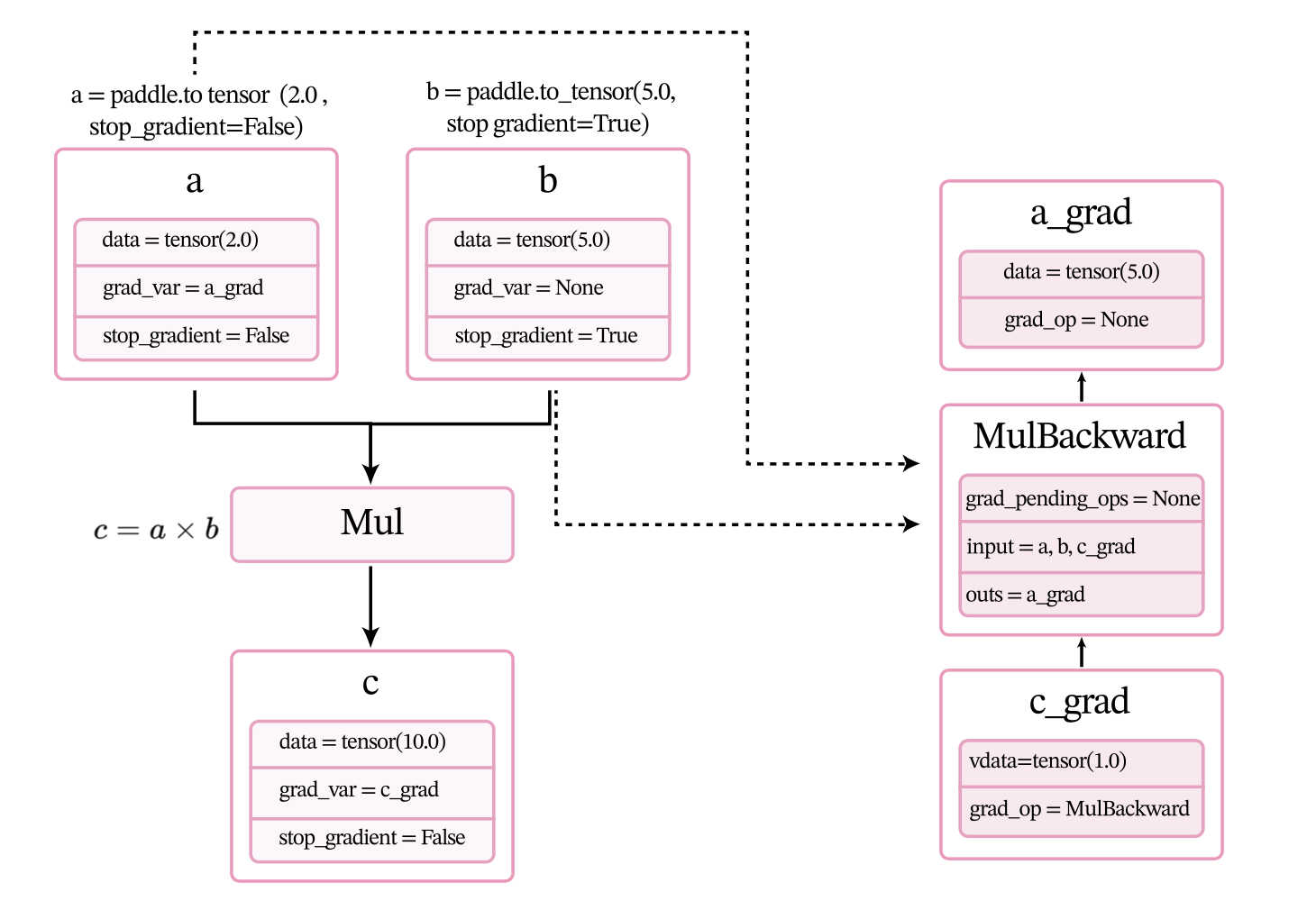
1.3.2.2 反向执行

调用backward()后，执行计算图上的反向过程，即通过链式法则自动计算每个张量或算子的微分，计算过程如图1.9所示。经过自动反向梯度计算，获得c_grad和a_grad的值。

图1.9 调用backward()后的计算图状态

1.3.3 预定义的算子

从零开始构建各种复杂的算子和模型是一个很复杂的过程，在开发的过程中也难以避免地会出现很多冗余代码，因此飞桨提供了基础算子和中间算子，可以便捷地实现复杂模型。

在深度学习中，大多数模型都是以各种神经网络为主，由一系列层(Layer)组成，层是模型的基础逻辑执行单元。飞桨提供了paddle.nn.Layer类来方便快速地实现自己的层和模型。模型和层都可以基于paddle.nn.Layer扩充实现，模型只是一种特殊的层。

当我们实现的算子继承paddle.nn.Layer类时，就不用再定义backward函数。飞桨的自动微分机制可以自动完成反向传播过程，让我们只关注模型构建的前向过程，不必再进行烦琐的梯度求导。

1.3.4 本书中实现的算子

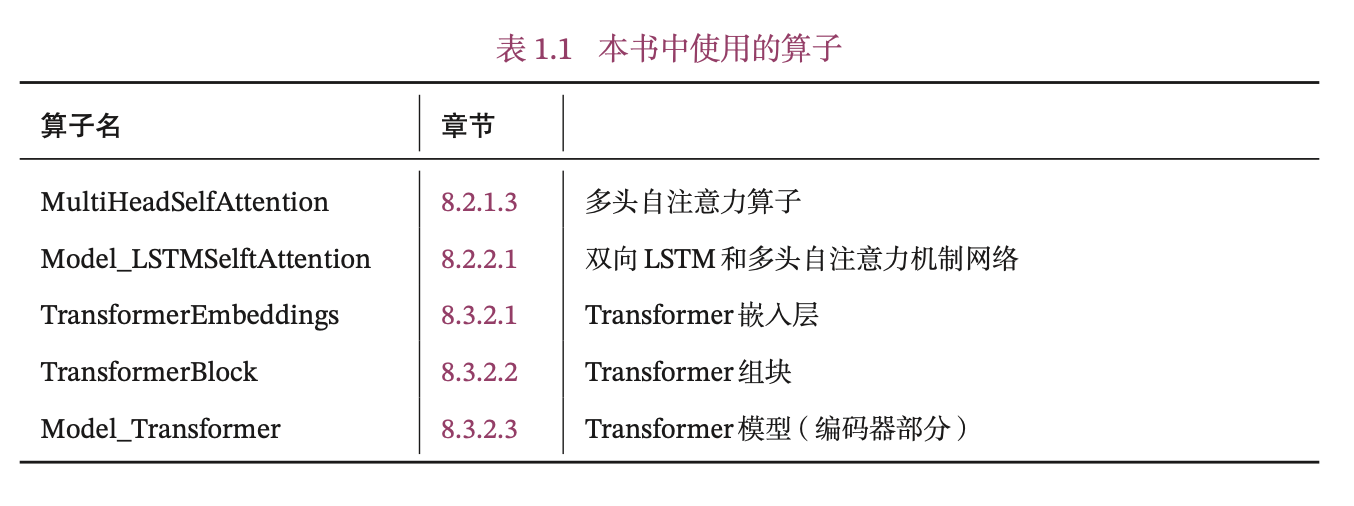
更深入的理解深度学习的模型和算法，在本书中，我们也手动实现自己的算子库：nndl，并基于自己的算子库来构建机器学习模型。本书中的自定义算子分为两类：一类是继承在第1.3.1节中定义Op类，这些算子是为了进行更好的展示模型的实现细节，需要自己动手计算并实现其反向函数；另一类是继承飞桨的paddle.nn.Layer类，更方便地搭建复杂算子，并和飞桨预定义算子混合使用。

本书中实现的算子见表1.1所示，其中Model_开头为完整的模型。

表1.1 本书中使用的算子

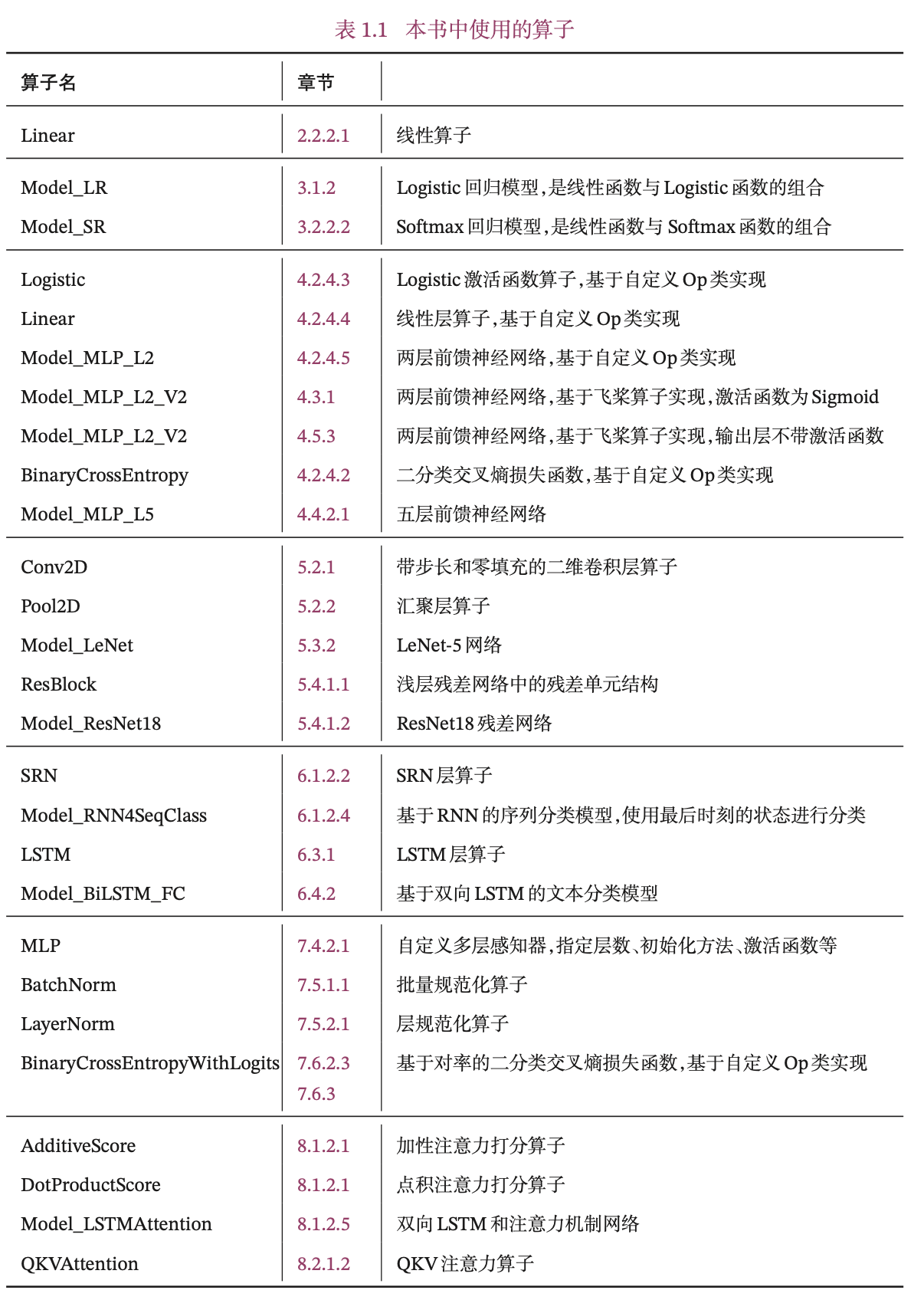
1.3.5 本书中实现的优化器

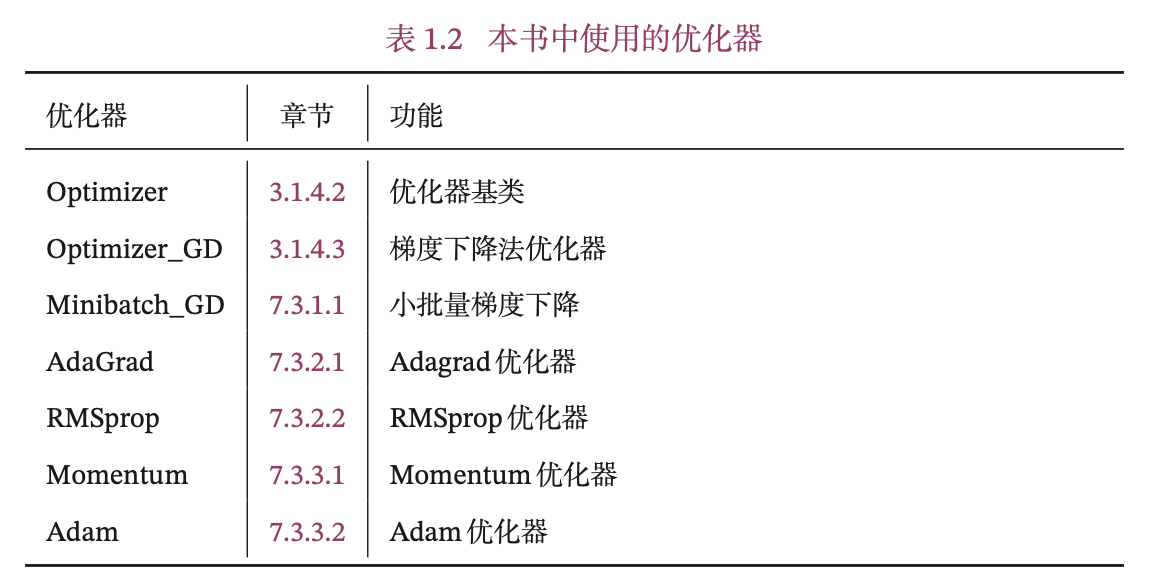
针对继承Op类的算子的优化，本书还实现了自定义的优化器，见表1.2所示。

表1.2 本书中使用的优化器

1.4 本书中实现的DataSet类

为了更好地实践，本书在模型解读部分主要使用简单任务和数据集，在案例实践部分主要使用公开的实际案例数据集。下面介绍我们用到的数据集以及对应构建的DataSet类。

1.4.1 数据集

本书中使用的数据集如下：

线性回归数据集ToyLinear150：在第2.2.1.2节中构建，用于简单的线性回归任务。ToyLinear150数据集包含150条带噪音的样本数据，其中训练集100条、测试集50条，由在第2.2.1.2节中create_toy_data函数构建。
非线性回归数据集ToySin25：在第2.3.1节中构建，用于简单的多项式回归任务.ToySin25数据集包含25条样本数据，其中训练集15条、测试集10条。ToySin25数据集同样使用在第2.2.1.1节中create_toy_data函数进行构建。
波士顿房价预测数据集：波士顿房价预测数据集共506条样本数据，每条样本包含了12种可能影响房价的因素和该类房屋价格的中位数。该数据集在第2.5节中使用。
二分类数据集Moon1000：在第3.1中构建，二分类数据集Moon1000数据是从两个带噪音的弯月形状数据分布中采样得到，每个样本包含2个特征，其中训练集640条、验证集160条、测试集200条。该数据集在本书第3.1节和第4.2节中使用。数据集构建函数make_moons在第7.4.2.3节和第7.6节中使用。
三分类数据集Multi1000：在第3.2.1节中构建三分类数据集集Multi1000，其中训练集640条、验证集160条、测试集200条。该数据集来自三个不同的簇，每个簇对应一个类别。
鸢尾花数据集：鸢尾花数据集包含了3种鸢尾花类别(Setosa、Versicolour、Virginica)，每种类别有50个样本，共计150个样本。每个样本中包含了4个属性：花萼长度、花萼宽度、花瓣长度以及花瓣宽度。该数据集在第3.3节和第4.5节使用。
MNIST数据集：MNIST手写数字识别数据集是计算机视觉领域的经典入门数据集，包含了训练集60 000条、测试集10 000条。MNIST数据集在第5.3.1节和第7.2节中使用。
CIFAR-10 数据集：CIFAR-10数据集是计算机视觉领域的经典数据集，包含了10种不同的类别、共 60 000 张图像，其中每个类别的图像都是6 000 张，图像大小均为32×32像素。CIFAR-10数据集在第5.5节中使用.
IMDB电影评论数据集：IMDB电影评论数据集是一份关于电影评论的经典二分类数据集。IMDB按照评分的高低筛选出了积极评论和消极评论，如果评分≥7，则认为是积极评论；如果评分≤4，则认为是消极评论。数据集包含训练集和测试集数据，数量各为25 000 条，每条数据都是一段用户关于某个电影的真实评价，以及观众对这个电影的情感倾向。IMDB数据集在第6.4节、第8.1节和第8.2节中使用.
数字求和数据集DigitSum：在第6.1.1节中构建，包含用于数字求和任务的不同长度的数据集。数字求和任务的输入是一串数字，前两个位置的数字为0-9，其余数字随机生成(主要为0)，预测目标是输入序列中前两个数字的加和，用来测试模型的对序列数据的记忆能力。
LCQMC通用领域问题匹配数据集：LCQMC数据集是百度知道领域的中文问题匹配数据集，目的是为了解决在中文领域大规模问题匹配数据集的缺失。该数据集从百度知道不同领域的用户问题中抽取构建数据。LCQMC数据集共包含训练集238 766条、验证集8 802条和测试集12 500 条。LCQMC数据集在第8.3节中使用。

1.4.2 Dataset类

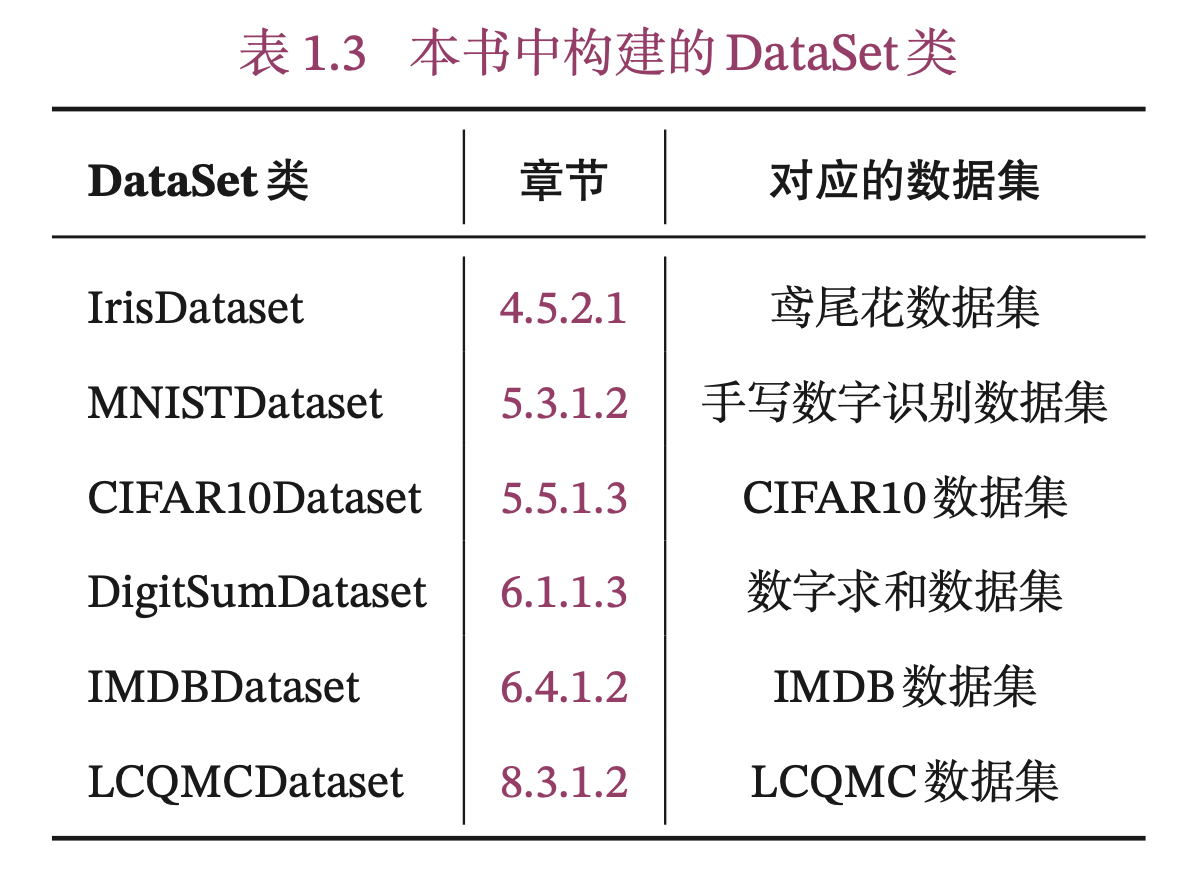
为了更好地支持使用随机梯度下降进行参数学习，我们构建了DataSet类，以便可以更好地进行数据迭代。

本书中构建的DataSet类见表1.3。关于Dataset类的具体介绍见第4.5.1.1节。

表1.3 本书中构建的DataSet类

1.5 本书中使用的Runner类

在一个任务上应用机器学习方法的流程基本上包括：数据集构建、模型构建、损失函数定义、优化器定义、评价指标定义、模型训练、模型评价和模型预测等环节。为了将上述环节规范化，我们将机器学习模型的基本要素封装成一个Runner类，使得我们可以更方便进行机器学习实践。除上述提到的要素外，Runner类还包括模型保存、模型加载等功能。Runner类的具体介绍可参见第2节.
这里我们对本书中用到的三个版本的Runner类进行汇总，说明每一个版本Runner类的构成方式.