1 何谓逆波兰表达式
逆波兰表达式又称为后缀表达式,是波兰逻辑学家J・卢卡西维兹(J・ Lukasewicz)于1929年首先提出的一种表达式的表示方法。
例如:
1 + 2 + 3,转换为逆波兰表达式:1 2 3 + +。
1 + 2 * 3,转换为逆波兰表达式:1 2 3 * +。
对于我们而言,中缀表达式是最熟悉也是最直观的一种求值方式,但是计算机处理中缀表达式并不方便。
对于计算机而言,逆波兰表达式是最优、最简洁、最方便检索的一种表达式形式。因为逆波兰表达式没有括号,并且严格遵循从左到右运算。只需要利用栈的特点,就可以一次性求出逆波兰表达式的值。
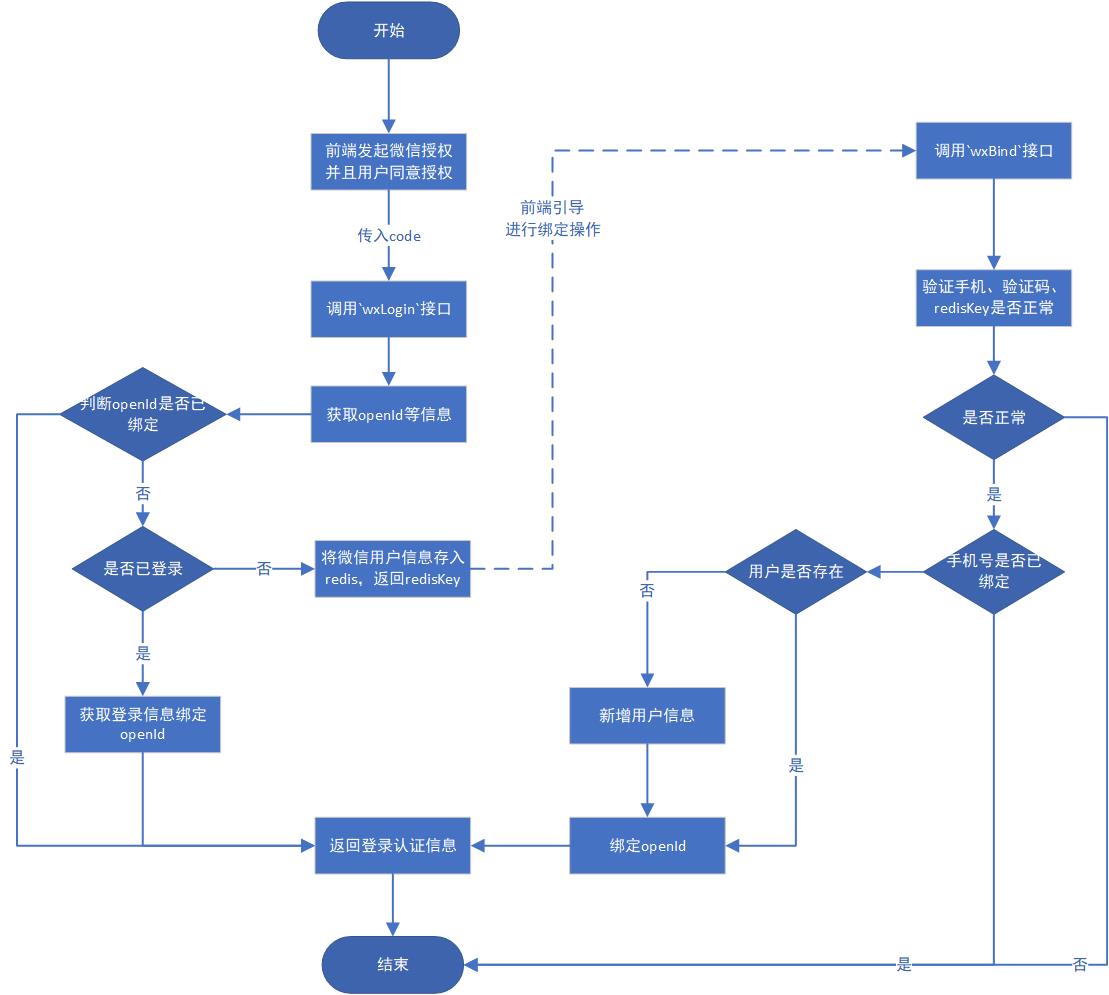
2 算法实现
首先需要一个队列用来存储后缀表达式,一个栈临时存储操作符。
- 构造一个运算符优先表(算符优先矩阵)。
- 读入一个中缀表达式并进行预处理,将运算符与操作数分隔开。
- 从左到右扫描中缀表达式。
- 如果是操作数,直接入队列;
- 如果是操作符,栈为空的情况下直接入栈;
- 不为空则需要比较栈顶运算符与当前运算符优先级,当前运算符优先级高则入栈;
- 否则将栈顶运算符出栈直到栈为空或者栈顶运算符优先级小于当前运算符。
- 计算逆波兰表达式结果。
3 C++实现代码
#include<bits/stdc++.h>
using namespace std;// 从操作符到索引的映射
map<char, int>operator_to_index;
// 算符优先矩阵
int priority_matrix[6][6] = {1, 1, -1, -1, -1, 1,1, 1, -1, -1, -1, 1,1, 1, 1, 1, -1, 1,1, 1, 1, 1, -1, 1,-1, -1, -1, -1, -1, 0,1, 1, 1, 1, 100, 1
};
// 输入的中缀表达式
string expression;
// 存储操作数
queue<string>Operand;
// 存储操作符
stack<char>Operator;
// 存储后缀表达式计算结果
stack<int>result;// 判断是否为操作符
bool isOperator(char ch) {if (ch == '(' || ch == ')' || ch == '+' || ch == '-' || ch == '*' || ch == '/')return true;return false;
}// 判断优先级
bool priority(char left, char right) {//左边操作符(栈顶)优先级低if (priority_matrix[operator_to_index[left]][operator_to_index[right]] == -1)return true;//左边操作符(栈顶)优先级与右边(当前操作符)相等if (priority_matrix[operator_to_index[left]][operator_to_index[right]] == 0)return true;return false;
}// 初始化
void init() {// 将操作符映射为对应的索引operator_to_index['+'] = 0;operator_to_index['-'] = 1;operator_to_index['*'] = 2;operator_to_index['/'] = 3;operator_to_index['('] = 4;operator_to_index[')'] = 5;
}// 打印后缀表达式
void print_postfix() {queue<string>temp = Operand;cout << "逆波兰表达式为:" << endl;while (!Operand.empty()) {cout << Operand.front() << ' ';Operand.pop();}cout << endl;Operand = temp;
}void print_Infix() {cout << "中缀表达式为:" << endl;cout << expression << endl;
}// 输入函数
bool readin() {cin >> expression;if (expression == "end")return false;return true;
}// 处理函数
void treat() {// 预处理表达式,将数字与操作符用空格分开for (int i = 0; i < expression.length(); i++) {if (isOperator(expression[i])) {expression.insert(i, " ");i++;expression.insert(i + 1, " ");}}stringstream sin(expression);string word;// 遍历表达式while (sin >> word) {// 如果是操作符if (isOperator(word[0])) {// 如果存储操作符的栈为空,直接入栈if (Operator.empty()) {Operator.push(word[0]);}// 如果栈顶运算符优先级小于当前运算符优先级,直接入栈else if (priority(Operator.top(), word[0])) {Operator.push(word[0]);}// 如果栈顶运算符优先级大于等于当前运算符优先级,则将栈顶出栈,直到栈为空或者栈顶运算符优先级小于当前运算符优先级else {while (!Operator.empty() && !priority(Operator.top(), word[0])) {string temp = "";temp += Operator.top();Operator.pop();Operand.push(temp);}// 右括号不入栈if (word[0] != ')')Operator.push(word[0]);else {// 将栈中左括号去除if (Operator.top() == '(')Operator.pop();}}}// 如果是操作数,直接进入Operand队列else {Operand.push(word);}}// 当操作符栈不为空时,需要将栈中操作符压入操作数队列中while (!Operator.empty()) {string temp = "";temp += Operator.top();Operator.pop();Operand.push(temp);}
}// 计算逆波兰表达式结果
void calculat() {queue<string>temp = Operand;// 依次遍历逆波兰表达式while (!Operand.empty()) {string s = Operand.front();Operand.pop();// 如果是操作符,则取出result栈中两个操作数,进行相应计算if (isOperator(s[0])) {int b = result.top();result.pop();int a = result.top();result.pop();int c = 0;if (s[0] == '+') {c = a + b;}else if (s[0] == '-') {c = a - b;}else if (s[0] == '*') {c = a * b;}else if (s[0] == '/') {c = a / b;}result.push(c);}// 如果是操作数,直接压入result栈else {result.push(stoi(s));}//cout << result.top() << ' ';}//cout << endl;Operand = temp;
}void print_result() {cout << "逆波兰表达式计算结果:" << endl;cout << result.top() << endl;cout << endl;
}int main() {init();cout << "请输入中缀表达式(end表示退出程序):" << endl;while (readin()) {treat();//print_Infix();print_postfix();calculat();print_result();}return 0;
}
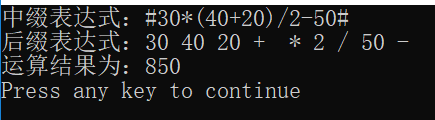
4 运算结果

附上输入样例:
1+(2+(3+4))
(1+2)6-(5+3)+(3+5)/4
(12+24+36)/12+100
(12+16/2-28+(20+7)/3)-10*2
注意:输入的中缀表达式不能有空格,因为是用cin读取的,cin不能读取空格。