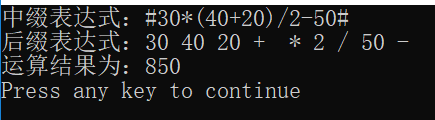
要求:设计一个算法,将一般算术表达式转化为逆波兰表达式,并求逆波兰表达式的值。
实现思路
- 获取一个中缀表达式
- 将表达式转换为后缀表达式
- 计算后缀表达式的结果
中缀表达式转换为后缀表达式的几个关键部分
假如不是运算符,则输出,否则进行下面步骤
- 假如遇到空栈或者‘(’时,直接入栈,并继续,因为第一个遇到的肯定是'#',所以直接入栈。
- 假如遇到'#',则说明表达式结束了,但得在前一点的后面进行判断。
- 假如遇到')',则进行出栈,知道遇到'(',并弹出,但不记录,因为我们不要括号的
- 优先级比较:
- 假如优先级大于栈顶,则入栈
- 小于或等于栈顶时,一直出栈,直到当前运算符优先级大于栈顶,则把当前运算符进栈。
计算后缀表达式
前一步已经将表达式存放在新的数组里面了,并且为了方便识别,在适当的位置都加了空格,方便识别。
由于需要进行计算,且要把char的数转换成一个整数,所以这里简单的利用一个整型数组,并且模拟栈的实现方式,基本思想如下:
- 对获取到后缀表达式进行扫描
- 如果为数字,则继续扫描直到遇到空格,并把数入栈。
- 假如为运算符,则进相应的运算,从栈中取出离栈顶最近的两个数,进行计算,并且把结果写在离栈顶较远的那个位置,并且把当前栈顶的数据清零。
- 最后获取到的结果会存放在数组的0位置。
结语
由于这个实验是我在学数据结构时的一个实验,刚学习编程,语言也比较混乱,如有错误的地方,欢迎指出。以下为代码部分:
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
/* (1)设计一个算法,将一般算术表达式转化为逆波兰表达式,并求逆波兰表达式的值。例如 #30*(40+20)/2-50# #为两个界限符
*/
const int StackSize = 30;
char result[30];//接收转换结果,并添加空格
char num;//用来result数组的计数//定义一个栈结构体
typedef struct Stack
{char data[StackSize];int top;
}StackType;//出栈处理,输入:栈结构体
char Pop(StackType *p)
{char x;if(p->top == -1) {printf("under flow\n");exit(0);}x = p->data[p->top--];return x;
}
//入栈处理
void Push(StackType *p, char dat)
{if(p->top == StackSize -1){printf("over flow\n");exit(0);}p->data[++p->top] = dat;
}//为空时返回1,不为空则返回0
bool Emtry(StackType *p)
{if(p->top == -1)return 1;return 0;
}
//获取栈顶的数据
char GetTop(StackType *p)
{if(p->top != -1)return p->data[p->top];return 0;
}//判断是运算符还是运算对象bool isNumber(char op){switch(op){ case ' ':case '(':case ')':case '+': case '-': case '*': case '/':case '#': return 0; default : return 1; }}
//获取运算符的优先级,1为最高,且统计优先级int priority(char ch){int value= 10; switch(ch){case '(':case ')': value = 4; break;//当遇到左括号时,所有的符号都会进行入栈处理,直到遇到右括号,或者内部运算输出case '*': value = 2; break;case '/': value = 2; break;case '+': value = 3; break;case '-': value = 3; break;case '#': value = 5; break;default: break;}return value;}/*
函数名:Nifix2Postfix
输 入:数组
返 回:无
功 能:将中缀表达式转换成后缀表达式并输出
*/
void Nifix2Postfix(char arr[])
{StackType* pStack = new StackType;pStack->top = -1;int i = 0;char ch;for(i=0;arr[i] != '\0';i++){if(isNumber(arr[i])){result[num++] = arr[i];}//不是对象时,即为运算符else{//首先判断是否为空,如果为空,则入栈if(Emtry(pStack) || arr[i] == '('){Push(pStack, arr[i]);continue;}if(arr[i] == '#')//结束符号break;if(arr[i] == ')')//出栈直到遇到({result[num++] = ' ';while((ch = Pop(pStack)) != '(' )//开始出栈,出到'('{result[num++] = ch;result[num++] = ' ';}continue;}result[num++] = ' ';//优先级比较ch = priority(GetTop(pStack)) - priority(arr[i]);//获取优先级比较后的结果,但ch>0时,运算符优先级大于栈顶,=0相等,<0小于//优先级大于栈顶if(ch > 0){//优先级大的入栈Push(pStack, arr[i]);}//优先级小于或等于栈顶else if(ch <= 0){//应该是出栈一个,然后判断优先级,假如不为空栈,继续判断优先级,然后将arr[i]入栈while( priority(arr[i]) >= priority(GetTop(pStack)))//此运算符优先级小于等于栈顶时,一直输出{
// printf("%c",ch = Pop(pStack));result[num++] = Pop(pStack);
// printf(" ");result[num++] = ' ';}Push(pStack, arr[i]); }}}while(GetTop(pStack) != '#'){result[num++] = ' ';result[num++] = Pop(pStack);}for(i=0;i<num;i++)printf("%c",result[i]);
}/*
函数功能:计算后缀表达式的值
输入:一个后缀表达式
输出:结果
*/
int Calculate(char arr[])
{int i, cal[10],top=-1;memset(cal,0,sizeof(cal));for(i=0;i<num;i++){if(isNumber(arr[i]))//判断是否是操作符,返回1不是,进来的只能是数字{//模拟入栈top++;while(arr[i] != ' ')//获取一个整数,并入栈{cal[top] = cal[top]*10 + arr[i++]-48;}}else{switch(arr[i]){//模拟出栈case '+': cal[top-1] = cal[top-1] + cal[top]; cal[top--] = 0; break;case '-': cal[top-1] = cal[top-1] - cal[top]; cal[top--] = 0; break;case '*': cal[top-1] = cal[top-1] * cal[top]; cal[top--] = 0; break;case '/': cal[top-1] = cal[top-1] / cal[top]; cal[top--] = 0; break;default: break;}}}return cal[0];
}int main(void)
{char express[] = "#30*(40+20)/2-50#";// gets(express);printf("中缀表达式:");printf("%s\n", express);printf("后缀表达式:");Nifix2Postfix(express);printf("\n");printf("运算结果为:%d\n", Calculate(result));return 0;
}运行结果: