版权声明:本文为博主原创文章,未经博主允许不得转载。https://blog.csdn.net/weixin_38451800/article/details/87982400
本文,主要的目的向大家介绍容积卡尔曼(CKF)算法,包括两方面:(1)将积分形式变换成球面径向积分形式的缘故;(2)三阶球面径向准则;最后给出一个非线性系统的例子和源代码,供大家参考使用。
1.参考资料
首先,还是给出一篇参考论文:湖南大学-段洋2018年的硕士毕业论文
链接:https://pan.baidu.com/s/18_BUWrpg4gNpZiOjUk2byA 提取码:8u89 。
(备注:其实,随便找一篇只要是没有太多错误的论文就好,只不过他这篇论文中还有:加了平方根的容积卡尔曼,即SRCKF)
然后,推荐一篇博客,好像并没有专门并且讲的很详细的博客。
2.容积卡尔曼(CKF)算法
容积卡尔曼滤波(Cubature Kalman filter, CKF),是由加拿大学者 Arasaratnam 和 Haykin 在 2009 年首次在硕士学位论文提出,CKF 基于三阶球面径向容积准则,并使用一组容积点来逼近具有附加高斯噪声的非线性系统的状态均值和协方差,是理论上当前最接近贝叶斯滤波的近似算法,是解决非线性系统状态估计的强有力工具。其中,将积分形式变换成球面径向积分形式和三阶球面径向准则是最为重要的两个步骤。
(1) 那**为何将积分形式变换成球面径向积分形式???**我们先来看看,原来的积分形式是啥样(如下图1):
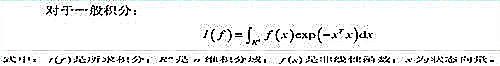
图1
为了解上式,我们有多少种方法呢?比如EKF是靠非线性函数线性化,泰勒级数取前几项近似,所以都不涉及到解积分方程,有人可能会问,哪里来的积分方程,那微分方程和积分方程不是一样的解法吗,况且有的时候积分方程比微分方程更容易求解;UKF是靠对非线性函数的概率密度分布进行近似,用一系列确定样本来逼近状态的后验概率密度;粒子滤波是靠频率代替概率;神经网络直接不管这些,三层结构用数据训练模型等等。然后,我们看看球面径向积形式(如下图):

图 2
(备注:这种形式变换的目的是什么呢?跟所有坐标变换的目的一样,即模型描述的简洁程度不同,讲深了这篇博客博主就跑偏了,哈哈哈)
(2) 高斯-厄米准则(Gass-Hermite,GH)和三阶球面径向容积准则
对图2径向式和球面积分式,分别利用Mr点的GH准则和Ms点的球面准则,可得

图3
3.权值和容积点
应用三阶球面径向容积准则,Mr=1,Ms=2n(n为状态向量维数),标准高斯积分可表示如下: 
比如n=3时,相应的容积点集为:[1,0,0,-1,1,0;
0,1,0,0,-1,0;
0,0,1,0,0,-1];
比如n=2时,相应的容积点集为:[1,0,-1,0;
0,1,0,-1];
4.一个CKF例子
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 容积Kalman滤波% 状态方程:x(:,k+1) = F * x(:,k) +[sqrt(Q) * randn;0]; % 观测方程:z(k+1) = atan(0.1 * x(1,k+1)) + sqrt(R) * randn; % 编程人:a往南向北,日期:2019/02/26 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%clc; clear all;close all;n=501;tf = 500; % 模拟长度 x=zeros(2,n);z=zeros(1,n);x(:,1) =[1;0.1]; % 初始状态 x_ckf=zeros(2,n);% x_estimate(:,1) = [1;0.1]; %状态的估计x_ckf(:,1)=[1;0.1];% e_x_estimate = x_estimate(:,1); %EKF的初始估计xhat=x_ckf(:,1);x_e_error=zeros(1,n);x_c_error=zeros(1,n);z_e_error=zeros(1,n);z_c_error=zeros(1,n);Q = 0.0001; % 过程状态协方差 R = 0.16; % 测量噪声协方差 P =[0.0099,0;0,0.0001]; %初始估计方差Pplus=P;F=[1,1;0,1];Gamma=[0.5;1];w=0.25; kesi=sqrt(2)*[1,0,-1,0;0,1,0,-1];for k = 1 : tf % 模拟系统 x(:,k+1) = F * x(:,k) + Gamma * sqrt(Q) * randn; %状态值 %x(:,k+1) = F * x(:,k) +[sqrt(Q) * randn;0]; z(k+1) = atan(0.1 * x(1,k+1)) + sqrt(R) * randn; %观测值end;for k = 1 : tf %Cubature卡尔曼滤波器%%%%%(1)求协方差矩阵平方根S=chol(Pplus,'lower');%%%%%(2)计算求容积点rjpoint(:,1)=S*kesi(:,1)+xhat;rjpoint(:,2)=S*kesi(:,2)+xhat;rjpoint(:,3)=S*kesi(:,3)+xhat;rjpoint(:,4)=S*kesi(:,4)+xhat;%%%%%(3)传播求容积点Xminus(:,1)=F*rjpoint(:,1); %容积点经过非线性函数后的值Xminus(:,2)=F*rjpoint(:,2);Xminus(:,3)=F*rjpoint(:,3); Xminus(:,4)=F*rjpoint(:,4); %%%%(4)状态预测xminus=w*Xminus(:,1)+w*Xminus(:,2)+w*Xminus(:,3)+w*Xminus(:,4);%%%%(5)状态预测协方差阵Pminus=w*(Xminus(:,1)*Xminus(:,1)'+Xminus(:,2)*Xminus(:,2)'+Xminus(:,3)*Xminus(:,3)'+Xminus(:,4)*Xminus(:,4)')-xminus*xminus'+Gamma * Q* Gamma';%Pminus=w*(Xminus(:,1)*Xminus(:,1)'+Xminus(:,2)*Xminus(:,2)'+Xminus(:,3)*Xminus(:,3)'+Xminus(:,4)*Xminus(:,4)')-xminus*xminus'+[Q,0;0,0]; %%%%观测更新%%%%%(1)矩阵分解Sminus=chol(Pminus,'lower');%%%%%(2)计算求容积点rjpoint1(:,1)=Sminus*kesi(:,1)+xminus;rjpoint1(:,2)=Sminus*kesi(:,2)+xminus;rjpoint1(:,3)=Sminus*kesi(:,3)+xminus;rjpoint1(:,4)=Sminus*kesi(:,4)+xminus;%%%%%(3)传播求容积点Z(1)=atan(0.1*rjpoint1(1,1));Z(2)=atan(0.1*rjpoint1(1,2));Z(3)=atan(0.1*rjpoint1(1,3));Z(4)=atan(0.1*rjpoint1(1,4));% Z(:,4)=[atan(0.1*rjpoint1(1,4));0];%%%%%%%(4)观测预测zhat=w*(Z(1)+Z(2)+Z(3)+Z(4));%%%%(5)观测预测协方差阵%Pzminus=w*(Z(:,1)*Z(:,1)'+Z(:,2)*Z(:,2)'+Z(:,3)*Z(:,3)'+Z(:,4)*Z(:,4)')-zhat*zhat'+[R,0;0,Q];Pzminus=w*(Z(1)^2+Z(2)^2+Z(3)^2+Z(4)^2)-zhat^2+R;%%%%(6)互协方差阵Pxzminus=w*(rjpoint1(:,1)*Z(1)+rjpoint1(:,2)*Z(2)+rjpoint1(:,3)*Z(3)+rjpoint1(:,4)*Z(4))-xminus*zhat;%%%%(7)计算卡尔曼增益K=Pxzminus/Pzminus;%%%%(8)状态更新xhat=xminus+K*(z(k+1)-zhat);%%%%(9)状态协方差矩阵更新Pplus=Pminus-K*Pzminus*K';x_ckf(:,k+1)=xhat;endt = 0 : tf;figure;plot(t,x(1,:),'k.',t,x_ckf(1,:),'g');legend('真实值','CKF估计值');
5.输出结果
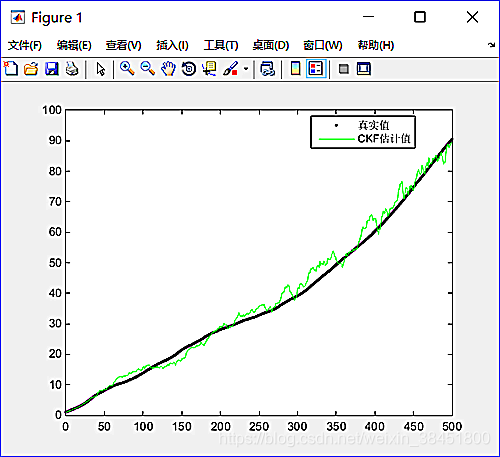 ,
,