希望对大家有帮助,文档做过修改。
1、辑模式:
在一般模式中可以进行删除、复制、粘贴等的操作,但是却无法编辑文件的内容,只有当到你按下【i, I, o, O, a, A, r, R】等任何一个字母之后才会进入编辑模式。这时候屏幕的左下方会出现【INSERT或 REPLACE】的字样,此时才可以进行编辑。而如果要回到一般模式时, 则必须要按下【Esc】即可退出编辑模式。
2、命令行模式:
输入【 : / ? 】三个中的任何一个,就可以将光标移动到最底下那一行。在这个模式中, 可以提供查找、读取、存盘、替换字符、离开vi、显示行号等的动作则是在此模式中完成的!
3、打开文件
# vim /path/to/somefile
vim +# :打开文件,并定位于第#行
vim +:打开文件,定位至最后一行
vim +/PATTERN : 打开文件,定位至第一次被PATTERN匹配到的行的行首
一般模式可用的按钮说明
4、移动光标
【h、j、k、l】,分别控制光标左、下、上、右移一格
翻屏
Ctrl+f: 向下翻一屏
Ctrl+b: 向上翻一屏
Ctrl+d: 向下翻半屏
Ctrl+u: 向上翻半屏
【n<space>】光标向右移动n个字符
【Home】移动到这一行的最前面字符处:0数字,但不能用数字小键盘上的数字
【End】 移动到这一行的最后面字符处:$,我测试好像不行
【w】光标跳到下个字的开头
【e】光标跳到下个字的字尾
【H】 光标移动到这个屏幕的最上方那一行的第一个字符
【M】 光标移动到这个屏幕的中间那一行的第一个字符
【L】光标移动到这个屏幕的最下方那一行的第一个字符
【G】 移动到这个文件的最后一行
【nG】移动到这个文件的第n行(可配合:set nu)
【gg】 移动到这个文件的第一行,相当于1G
【n<Enter>】光标向下移动n行
5、查找与替换
【/word】 向光标向下寻找一个名称为word的字符串
【?word】 向光标向上寻找一个名称为word的字符串
【n】 代表重复前一个查找的动作
【N】 与n刚好相反,为【反向】进行行前一个查找动作
【:n1,n2s/word1/word2/g】 n1与n2为数字,在第n1与n2行之间查找word1 这个字符串,并将该字符串替换为word2
【:1,$s/word1/word2/g】 从第一行到最后一行查找word1字符串,并将该字符串替换为word2
【:1,$s/word1/word2/gc】 从第一行到最后一行查找word1字符串,并将该字符串替换为word2 ,且在替换前提示用户确认是否进行替换
6、删除、复制与粘贴
【x】 为向后删除一个字符 (相当于【del】键)
【X】 为向前删除一个字符(相当于【backspace】键)
【nx】 连续向后删除n个字符
【dd】 删除光标所在行
【dn】 删除光标所在的向下n行
【d1G】 删除光标所在行到第一行的所有数据
【dG】 删除光标所在到最后一行的所有数据
【d$】 删除光标所在处,到该行的最后一个字符
【d0】 删除光标所在处,到该行的最前一个字符
【yy】 复制光标所在的那一行
【nyy】 复制光标所在的向下n列
【y1G】 复制光标所在行到第一行的所有数据
【yG】 复制光标所在行到最后一行的所有数据
【y0】 复制光标所在的那个字符到该行行首的所有数据
【y$】 复制光标所在的那个字符到该行行尾的所有数据
【p】将已复制的数据在光标下一行粘贴上
【P】 则为贴在光标的上一行
【u】 恢复前一个操作
【Ctrl+r】重做上一个操作
【.】 是重复前一个操作
7、一般模式切换到编辑模式的可用的按钮说明
【i, I】 进入编辑模式:
i 为【从目前光标所在处插入】
I 为【在目前所在行的第一个非空格符处开始插入】
【a, A】 进入编辑模式(Insert mode):
a 为【从目前光标所在的下一个字符处开始插入】
A 为【从光标所在行的最后一个字符处开始插入】
【o, O】 进入编辑模式:
o 为【在目前光标所在的下一行处插入新的一行】
O 为在目前光标所在处的上一行插入新的一行
【r, R】 进入取代模式:
r 只会取代光标所在的那一个字符一次
R会一直取代光标所在的文字,直到按下 ESC 为止;
【Esc】 退出编辑模式,回到一般模式
8、一般模式切换到命令行模式可用的按钮说明
【:w】 保存编辑的内容
【:w!】强制写入该文件,但跟你对该文件的权限有关
【:q】 离开vi
【:q!】 不想保存修改强制离开
【:wq】 保存后离开
【:x】 保存后离开
【ZZ】 若文件没有更动,则不保存离开,若文件已经被更改过,则保存后离开
【:w filename】 将编辑的数据保存成另一个文件(类似另存)
【:r filename】 在编辑的数据中,读入另一个文件的数据。即将【filename】 这个文件的内容加到光标所在行后面。
【:n1,n2 w filename】 将n1到n2的内容保存成filename这个文件。
【:! command】暂时离开vi 到命令行模式下执行command的显示结果!例如 【:! ls /home】即可在 vi 当中察看/home底下以ls输出的文件信息!
【:set nu】 显示行号
【:set nonu】 与 set nu 相反,为取消行
9、vim的缓存文件、恢复与开启时的警告信息
我们知道一些常用的编辑软件,都有个恢复的功能,就是说当你的系统因为某些原因而导致类似当机的情况时,还可以利用这个恢复功能将之前未保存的数据找回来。我们的VIM也有这个功能。
当我们在使用vim编辑时,vim会在与被编辑的文件的目录下,再建立一个名为 .filename.swp的文件。如果你的系统因为某些原因断线了, 导致你编辑的文件还没有保存,这个时候 .filenam.swp 就能够发会救援的功能了。
我们来演示一下
在/jiaoben下面出现了一个.bincp.sh.swp 文件,其实这个文件是bincp.sh 文件没有保存,中断系统后出现的恢复文件,在下次编辑bincp.sh文件时,系统会自动提示是否从上次执行处继续执行,还是终止等,根据提示执行就可以,执行完成后,保存文档后记得把 .bincp.sh文件删除。删除命令:rm -f .bincp.sh ,下次再执行bincp.sh时就不会出现提示。

提示如下:
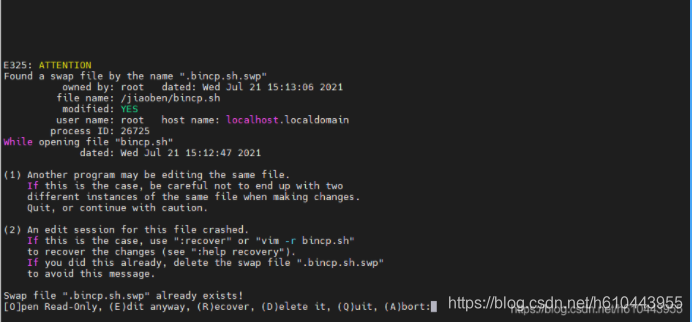
问题一:可能有其他人或程序同时在编辑这个文件:
问题二:在前一个vim的环境中,可能因为某些不知名原因导致vim中断 (crashed):
右下角会出现六个命令项,其作用说明如下:
(O)pen Read-Only:打开此文件成为只读档, 可以用在你只是想要查阅该文件内容并不想要进行编辑行为时。一般来说,在上课时,如果你是登入到同学的计算机去看他的配置文件, 结果发现其实同学他自己也在编辑时,可以使用这个模式;
(E)dit anyway:还是用正常的方式打开你要编辑的那个文件, 并不会载入暂存盘的内容。如果说两个人都在编辑这个文件的话,很容易出现互相改变对方的文件等问题。
(R)ecover:就是加载暂存盘的内容,用在你要救回之前未保存的工作。 不过当你救回来并且储存离开vim后,还是要手动自行删除那个暂存档。
(D)elete it:你确定那个暂存档是无用的!那么开启文件前会先将这个暂存盘删除
(Q)uit:按下 q 就离开vim,不会进行任何动作回到命令提示字符。
(A)bort:忽略这个编辑行为,感觉上与 quit 非常类似!
10、vim的功能
其实,目前大部分的Linux发行版本都以vim取代了vi。为什么要用vim呢?因为vim具有颜色显示的功能,并且还支持许多的程序语法(syntax)和相应的提示信息。查看自己的VI是不是被VIM代替,可以用
alias这个命令来查看是不是有alias vi=’vim’这一行。
11、块选择
【v】字符选择,会将光标经过的地方反白选择
【V】 行选择,会将光标经过的行反白选择
【Ctrl+v】 块选择,可以用长方形的方式选择资料 (提制竖列)
【y】 将反白的地方复制
【d】 将反白的地方删除
12、分屏显示一个文件
Ctrl+w, s: 水平拆分窗口 (按住Ctrl+w后松开键盘,按键盘上的s键就可以水平拆分)
Ctrl+w, v: 垂直拆分窗口 (按住Ctrl+w后松开键盘,按键盘上的v键就可以垂直拆分)
按住Ctrl+w键按两次就可以切换光标的不同的窗口
如果需要突出窗口可以输入exit 。
13、多文件编辑
大家在使用vim的时候,可能会碰到你需要复制一个文件中的某段到另外一个文件中,而vim不能够在关闭的时候,把这段保留住。或者是用其它的方法复制。
【vim file1 file2】
【:n】编辑下一个文件
【:N】编辑上一个文件
【:files】列出目前这个vim编辑的所有文件
多窗口功能
有两个需要对照着看的文件
【:sp filename】开启一个新窗口,如果有加 filename, 表示在新窗口开启一个新文件,否则表示两个窗口为同一个文件内容(同步显示)。
【ctrl+w+j】
【ctrl+w+↓】按键的按法是:先按下 【ctrl】 不放, 再按下 w 后放开所有的按键,然后再按下 j (或向下箭头键),则光标可移动到下方的窗口。
【ctrl+w+k】
【ctrl+w+↑】同上,不过光标移动到上面的窗口。
vim 环境设定与记录(~/.vimrc, ~/.viminfo)
14、参数参考文档。
- 设定自动缩进
:set autoindent
:set ai
:set noai - 查找到的文本高亮显示或取消
:set hlsearch
:set nohlsearch - 语法高亮
:syntax on
:syntax off -
显示忽略或区分字符大小写
:set ic
:set noic
-
显示或取消显示行号
:set nu
:set nonu
-
将另外一个文件的内容填充在当前文件中
:r /path/to/somefile
-
将当前文件中部分内容另存为另外一个文件末行模式下使用w命令
:w /path/to/somewhere
:ADDR1,ADDR2w /path/to/somewhere -
配置文件(保存退出vim后,在下次使用vim的时候,就会有自己的vim操作环境了。)
/etc/vimrc(全局配置有效)
~/.vimrc (当前bash)
注意;上面的参数参考中每一行前面加不加【:】效果都是一样的。
15、如果想自己专研vim 可以执行命令: vimtutor (此命令可以自己学习vim)
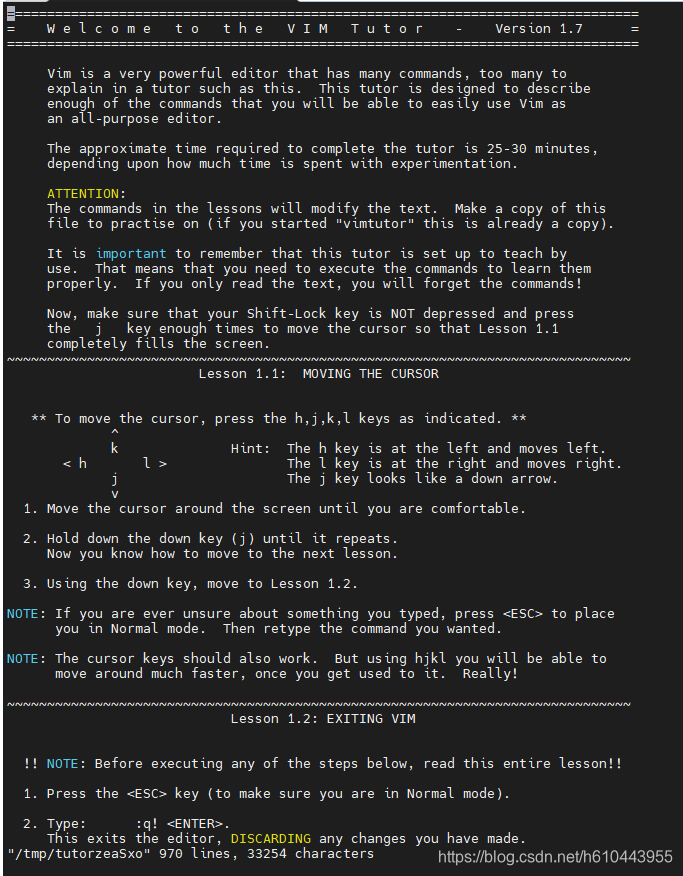
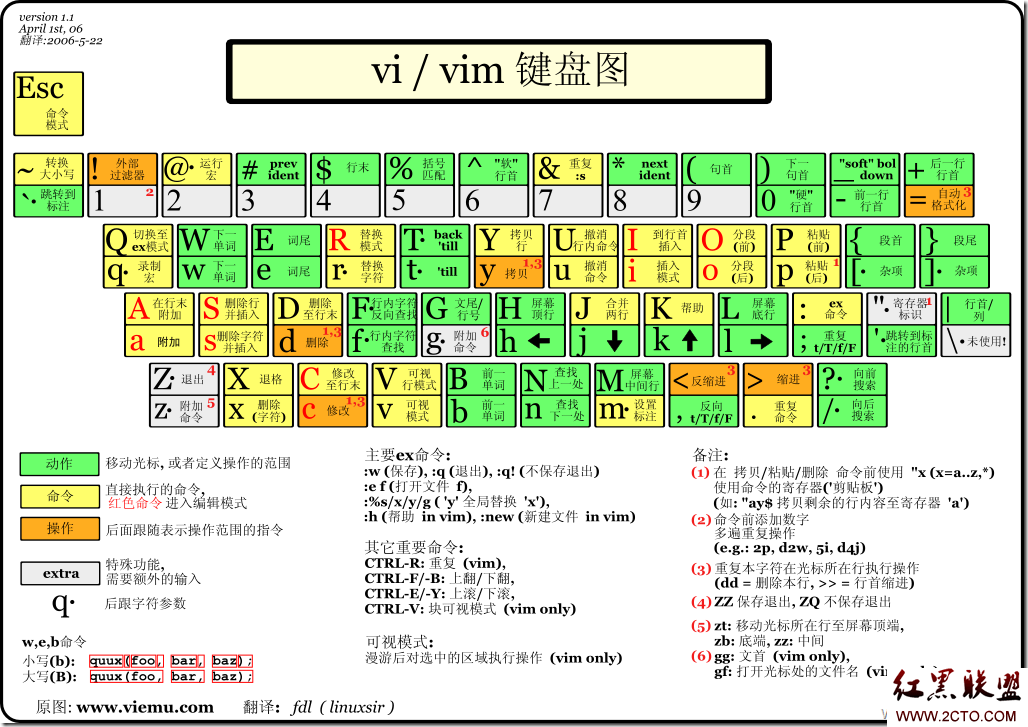
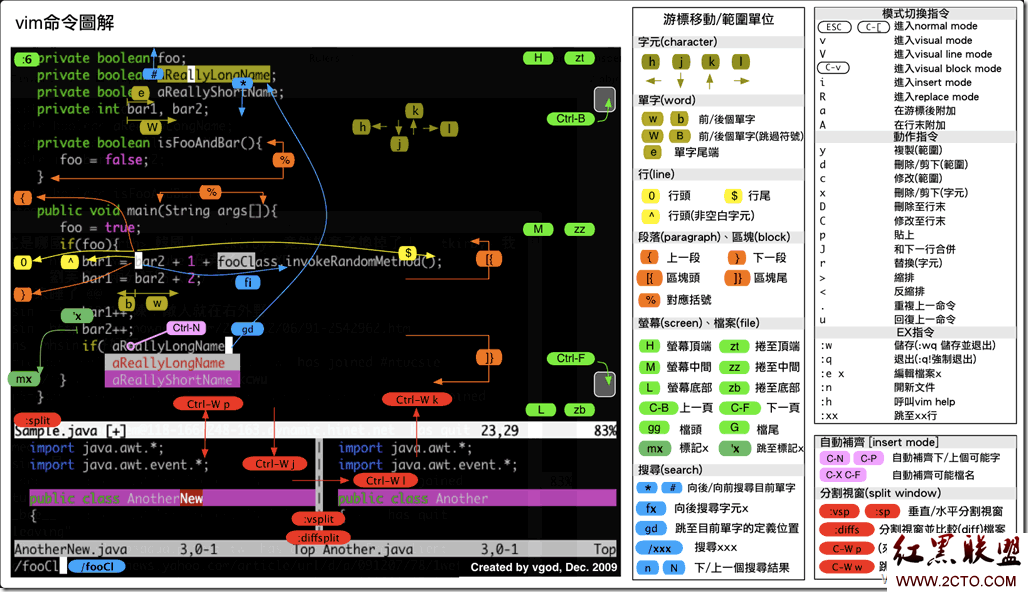
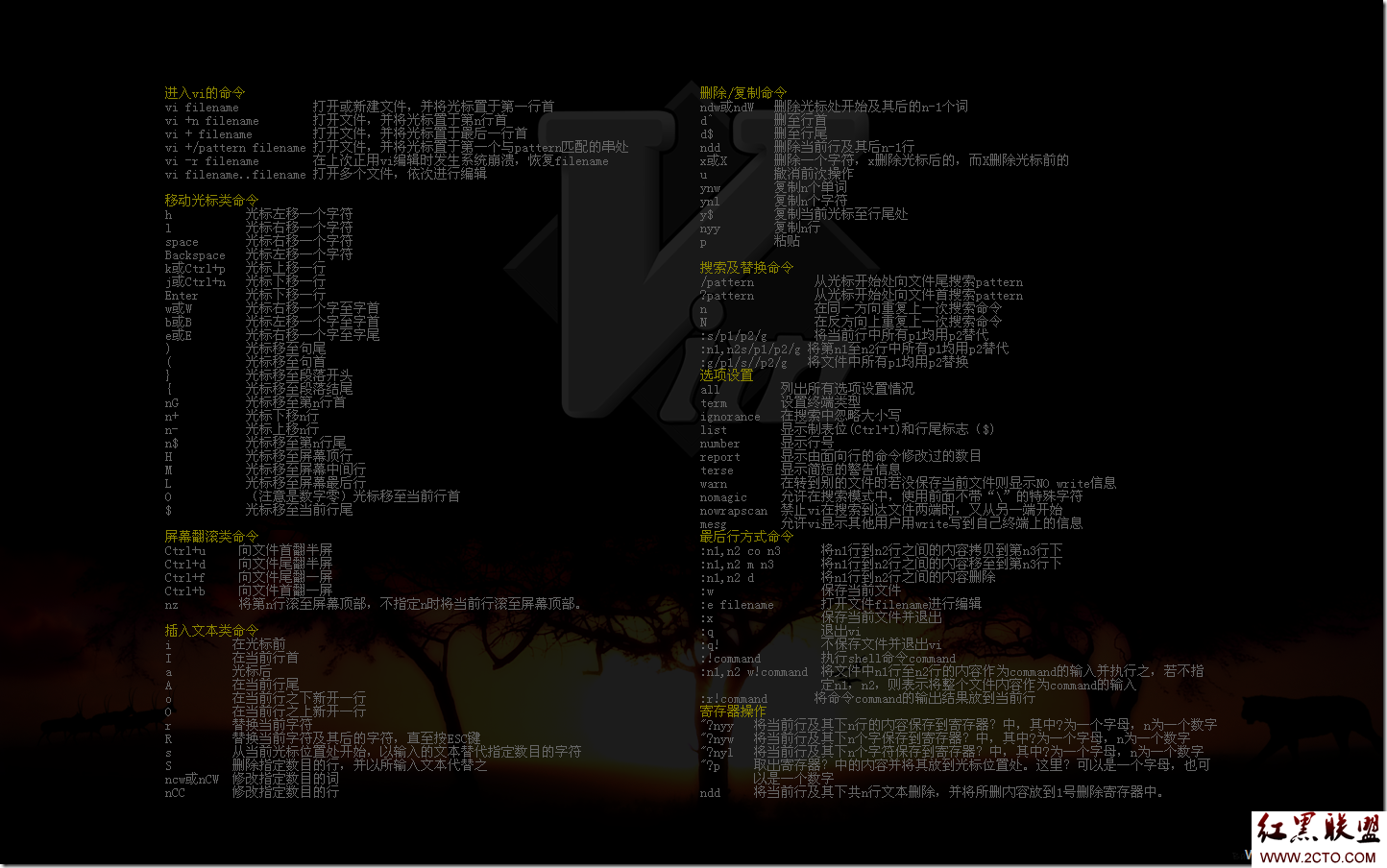
16、vi/vim键盘图