问题引入

数学描述

数学实现

最大似然原理（The Principle of Maximum Likelihood）

代码实现

问题求解：

非线性关系的线性化

问题求解

代码实现

结果

内置函数

示例（求解“问题引入”）

练习题：

问题引入

大家一定非常熟悉理想气体状态方程 $pV=nRT$ ,假如我们现在要研究理想气体压强p（ $N/m^{^{2}}$ ）和温度T（°C）的关系，在实验室测得了一系列数据如表一所示，那么我们该如何处理这些数据呢？

表一压强与温度对应表
T（°C）	-40	0	40	80	120	160
p（ $N/m^{^{2}}$ ）	6900	8100	9350	10500	11700	12800

由理想气体状态方程已知，当系统体积不变时，p和T成线性关系，处理这种数据的一个比较好的办法是本节所要讨论的方法——线性最小二乘回归。

数学描述

什么样的函数能最好的描述实验所得的数据点呢？当然是离所有数据点最近的函数！那么问题来了，什么样的函数才叫“离所有数据点最近”呢？

数学家们给出了残差（residual）的概念：实际观察值与估计值（拟合值）之间的差。

$e=y-a_{0}-a_{1}x$

这样一来，“离所有数据点最近”就好描述了，对于线性关系的数据点，我们只要找到一条直线使得所有有效数据点的残差之和达到最小即可！

可是这样描述有一个很大的缺陷，那就是正负残差会进行抵消，我们必须消除残差正负号的影响，在这里，我们考虑对残差进行平方求和，即

$S_{r}= \sum_{i=1}^{n}e_{i}^{2}=\sum_{i=1}^{n}(y_{i}-a_{0}-a_{1}x_{i})^{2}$

该方法即为最小二乘（least square）。

数学实现

为了确定 $a_{1}$ 和 $a_{0}$ 的值，我们需要利用 $S_{r}$ 达到最小这一条件。

对上式进行微分

$\frac{\partial S_{r}}{\partial a_{0}}=-2\sum (y_{i}-a_{0}-a_{1}x_{i})$ $\frac{\partial S_{r}}{\partial a_{0}}=-2\sum (y_{i}-a_{0}-a_{1}x_{i})$

$\frac{\partial S_{r}}{\partial a_{1}}=-2\sum [(y_{i}-a_{0}-a_{1}x_{i})x_{i}]$

令导数等于0，可以得到

$0=\sum y_{i}-\sum a_{0}-\sum a_{1}x_{i}$

$0=\sum x_{i}y_{i}-\sum a_{0}x_{i}-\sum a_{1}x_{i}^{2}$

联立求解可以得到 $a_{0},a_{1}$

$a_{1}=\frac{n\sum x_{i}y_{i}-\sum x_{i}\sum y_{i}}{n\sum x_{i}^{2}-(\sum x_{i})^{2}}$

带入到方程组可以得到

$a_{0}=\bar{y}-a_{1}\bar{x}$

这样就求出了 $a_{0},a_{1}$

最大似然原理（The Principle of Maximum Likelihood）

（1）在整个数据分布范围内，所有数据点与直线的距离都处于差不多的量级；

（2）数据点沿着直线分布符合正态分布

满足上述两个条件得出的 $a_{0},a_{1}$ 是最优的，回归线的标准差就可以有下式计算

$s_{y/x}=\sqrt{\frac{S_{r}}{n-2}}$

下标y/x是由给定的x估计y的误差。注意分母的n-2是必要的：计算Sr时用到了两个估计值 $a_{0},a_{1}$ ，因此损失了两个自由度。

另外一种误差也值得注意，那就是平均值与数据点之间的差

$S_{t}=\sum (y_{i}-\bar{y})^{2}$

两个误差都跟拟合程度有关，不妨将二者结合，这样就得出了决定系数（coefficient of determination）的概念

$r^{2}=\frac{S_{t}-S_{r}}{S_{t}}$

$r=\sqrt{r^{2}}$ 称为相关系数（Correlation coefficient）

$r=\frac{n\sum x_{i}y_{i}-\sum x_{i}\sum y_{i}}{\sqrt{n\sum x_{i}^{2}-(\sum x_{i})^{2}}\sqrt{n\sum y_{i}^{2}-(\sum y_{i})^{2}}}$

相关系数定量地刻画了x和y的相关程度，即r越大，相关程度越大；r=0,对应相关程度最低。

代码实现

function [a,r2]=linregr(x,y)
%linregr:线性回归拟合（linear regression curve fitting）
%       [a,r2]=linregr(x,y):对直线数据的最小二乘拟合%input:
%    x=自变量
%    y=因变量
% output:
%     a=a(1)-斜率；a(2)-截距
%     r2=决定系数n=length(x);
if length(y) ~= n, error("x向量和y向量必须等长");endx=x(:);y=y(:)
sx=sum(x);sy=sum(y);
sx2=sum(x.*x);sxy=sum(x.*y);sy2=sum(y.*y);
a(1)=(n*sxy-sx*sy)/(n*sx2-(sx)^2);%计算a1
a(2)=sy/n-a(1)*sx/n;%计算a2(文中的a0)
r2=((n*sxy-sx*sy)^2)/((n*sx2-(sx)^2)*(n*sy2-(sy)^2));%相关系数xp=linspace(min(x),max(x),20*n);
yp=a(1)*xp+a(2);
plot(x,y,'o',xp,yp)
grid on
end

问题求解：

将问题引入部分问题的数据带入

x=[-40	0	40	80	120	160];
y=[6900	8100	9350	10500	11700	12800];
[a,r2]=linregr(x,y)

获得拟合结果

>> linregr_test
a =1.0e+03 *0.0296    8.1152
r2 =0.9997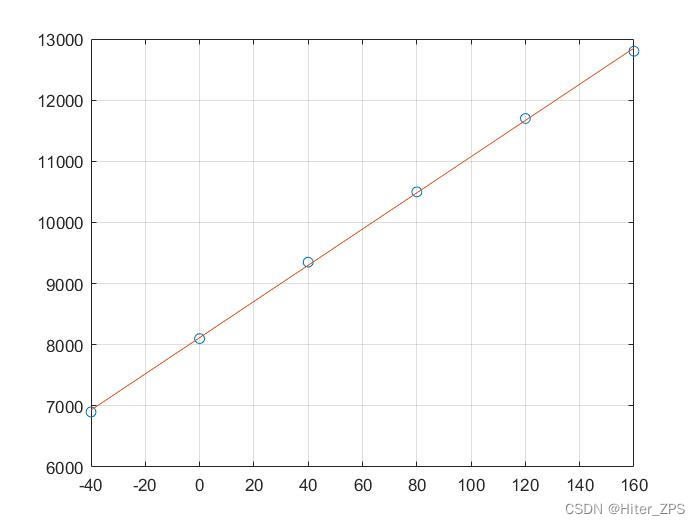

发现决定系数为0.9997，代表拟合的很好，这从拟合图像中也可以看出。

非线性关系的线性化

线性回归的用处很多，它还可以对非线性数据进行拟合！对于某些情况，我们可以将非线性转化为线性进行拟合，得到系数后利用反函数回到非线性。

指数方程（a）

$y=\alpha _{1}e^{\beta _{1}x}$

应用：人口增长，放射性衰变……

幂方程(b)

$y=\alpha _{2}x^{\beta _{2}}$

常用来描述基本模型未知的拟合。

饱和增长方程(c)

$y=\alpha _{3}\frac{x}{\beta _{3}+x}$

人口限制增长，生态环境……

上述模型均可以转换为线性形式，然后进行线性拟合。

例如，对指数模型线性处理：

$lny=ln\alpha _{1}+\beta _{1}x$

对幂方程线性化

$logy=\alpha _{2}log+\beta _{2}logx$

对饱和增长方程

$\frac{1}{y}=\frac{1}{\alpha _{3}}+\frac{\beta _{3}}{\alpha _{3}}\frac{1}{x}$

对应带入相关的a1,a0即可求出拟合关系。

问题求解

例一：人的表面积A与体重W和身高H有关。下对几个身高为180cm的志愿者进行了相关测量，得到表二

$W/kg$	70	75	77	80	82	84	87	90
$A/m^{2}$	2.10	2.12	2.15	2.20	2.22	2.23	2.26	2.30

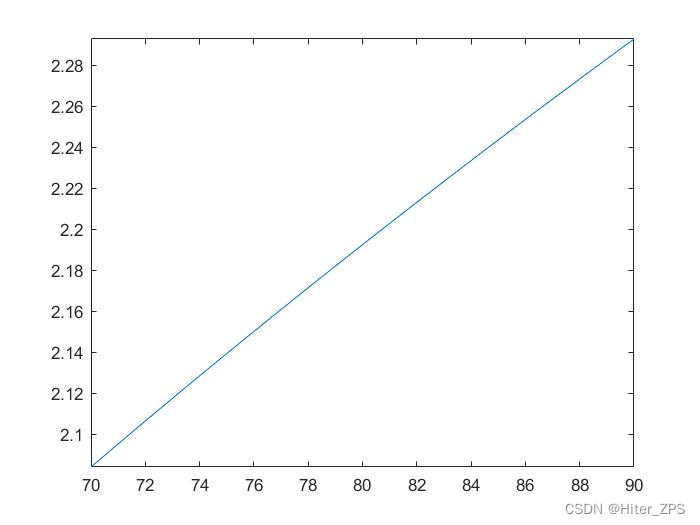
若数据非常适合用幂方程进行拟合： $A=aW^{b}$

（1）估计a,b的值并绘出拟合图；

（2）计算95kg的人的表面积。

代码实现

x=[70	75	77	80	82	84	87	90];
y=[2.10	2.12	2.15	2.20	2.22	2.23	2.26	2.30];
[a,r2] = linregr(log(x),log(y))figure(2)
A = @(W) exp(a(2)).*W.^(a(1));
fplot(A,[70,90])
exp(a(2)) * 95^(a(1))%W=95kg时的表面积

结果

>> linregr_test
a =0.3799   -0.8797
r2 =0.9711
ans =2.3404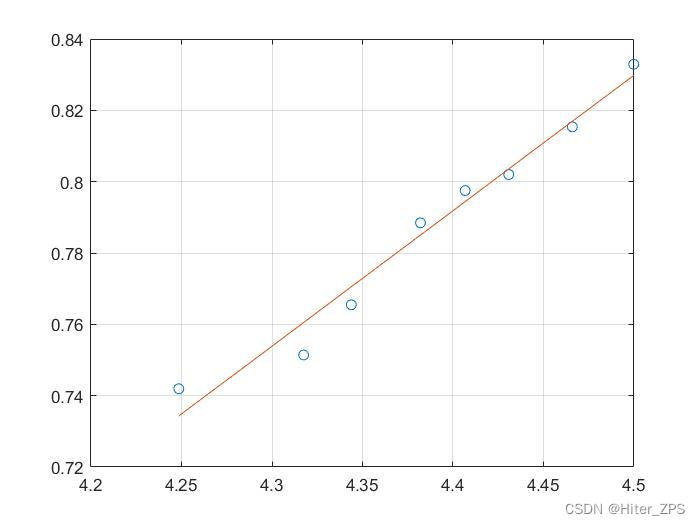

内置函数

MATLAB内置polyfit函数和polyval函数可以分别求解数据的n次最小二乘拟合多项式和特定点取值。

用法：

p=ployfit(x,y,n) 返回次数为 n 的多项式 p(x) 的系数，该阶数是 y 中数据的最佳拟合（在最小二乘方式中）。p 中的系数按降幂排列，p 的长度为 n+1

p(x)=p1xn+p2xn−1+...+pnx+pn+1

y=polyval(p,x) 计算多项式 p 在 x 的每个点处的值。参数 p 是长度为 n+1 的向量，其元素是 n 次多项式的系数（降幂排序）：

示例（求解“问题引入”）

x=[-40	0	40	80	120	160];
y=[6900	8100	9350	10500	11700	12800];
a=polyfit(x,y,1)
X=linspace(-40,160);
Y=polyval(a,X);
plot(x,y,'o',X,Y)

>> polyfit_test02
a =1.0e+03 *0.0296    8.1152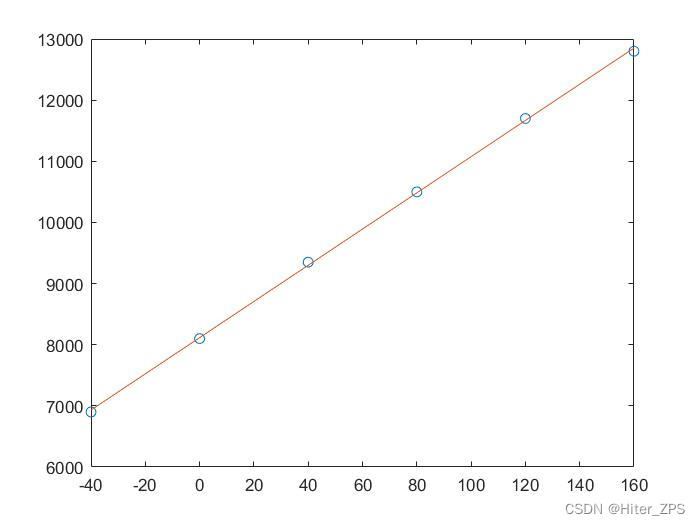

练习题：

1.研究人员考察细菌生长率k(每天)与氧气浓度c/(mg/L)的关系，得到实验数据表格如表三

c	0.5	0.8	1.5	2.5	4
k	1.1	2.5	5.3	7.6	8.9

提示：采用 $k=\frac{k_{max}c^{2}}{c_{s}+c^{2}}$ 进行拟合。

（1）利用线性回归估计cs和kmax；

（2）并计算c=2mg/L时的生长率。

2.理论上细菌在培养皿中的繁殖情况可以描述为

$\frac{dX}{dt}=\mu X$

式子中X表示细菌数量， $\mu$ 表示特定繁殖率。请根据表中数据估算 $\mu$

时间/h	0	1	2	3	4	5	6
细菌/(g/L)	0.100	0.335	1.102	1.655	2.453	3.702	5.460

声明：文章来源于笔者学习【美】Steven C. CHapra所著，林赐译《工程于科学数值方法的MATLAB实现》（第4版）的笔记，如有谬误或想深入了解，请翻阅原书。

MATLAB数值分析学习笔记：线性最小二乘回归

问题引入

数学描述

数学实现

最大似然原理（The Principle of Maximum Likelihood）

代码实现

问题求解：

非线性关系的线性化

问题求解

代码实现

结果

内置函数

示例（求解“问题引入”）

练习题：

相关文章

R语言实现偏最小二乘回归法 partial least squares (PLS)回归

偏最小二乘回归 Matlab

偏最小二乘回归预测(MATLAB源码)

MATLAB-偏最小二乘回归分析

MATLAB实现偏最小二乘回归PLS

第10章最小二乘线性回归分析

普通最小二乘（OLS）回归

最小二乘法：求回归直线方程

最小二乘回归

离线安装IE 11

Microsoft Edge离线安装包下载

安装IE11提示“Internet Explorer在安装前需要更新”

安装ie11提示计算机安装了更新的版本,离线安装IE11浏览器提示quot;获取更新quot;解决方法 - 191路由网...

electron离线安装

chrome浏览器离线安装包下载地址

如何下载谷歌浏览器官方最新离线安装包

【已解决】在Win11上离线安装 .NET Framework 3.5的方法【含网盘离线文件】

win11电脑安装ie11浏览器

Windows7安装IE11步骤和中文安装包超简单

IE11的安装方法和更新补丁