一、最小二乘法的历史

1801年，意大利天文学家朱赛普·皮亚齐发现了第一颗小行星谷神星。经过40天的跟踪观测后，由于谷神星运行至太阳背后，使得皮亚齐失去了谷神星的位置。随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星，但是根据大多数人计算的结果来寻找谷神星都没有结果。

只有时年24岁的高斯所计算的谷神星的轨道，被奥地利天文学家海因里希·奥尔伯斯的观测所证实，使天文界从此可以预测到谷神星的精确位置。同样的方法也产生了哈雷彗星等很多天文学成果。

高斯使用的方法就是最小二乘法，该方法发表于1809年他的著作《天体运动论》中。其实法国科学家勒让德于1806年独立发明“最小二乘法”，但因不为世人所知而默默无闻。1829年，高斯提供了最小二乘法的优化效果强于其他方法的证明。

二、最小二乘法的原理

最小二乘法的形式如下式：

标函数 $=\sum(\text { 观测值 }-\text { 理论值 })^{2}$

观测值就是我们的多组样本，理论值就是我们的假设拟合函数。目标函数也就是在机器学习中常说的损失函数，我们的目标是得到使目标函数最小化时候的拟合函数的模型。举一个最简单的线性回归的简单例子，比如我们有 $m$ 个只有一个特征的样本: $\left(x_{i}, y_{i}\right)(i=1,2,3 \ldots, m)$
样本采用一般的 $h_{\theta}(x)$ 为 $n$ 次的多项式拟合，

$h_{\theta}(x)=\theta_{0}+\theta_{1} x+\theta_{2} x^{2}+\ldots \theta_{n} x^{n}, \theta\left(\theta_{0}, \theta_{1}, \theta_{2}, \ldots, \theta_{n}\right)$ 为参数

最小二乘法就是要找到一组 $\theta\left(\theta_{0}, \theta_{1}, \theta_{2}, \ldots, \theta_{n}\right)$ 使得 $\sum_{i=1}^{n}\left(h_{\theta}\left(x_{i}\right)-y_{i}\right)^{2}$ (残差平方和)

最小，即，求 $\min \sum_{i=1}^{n}\left(h_{\theta}\left(x_{i}\right)-y_{i}\right)^{2}$

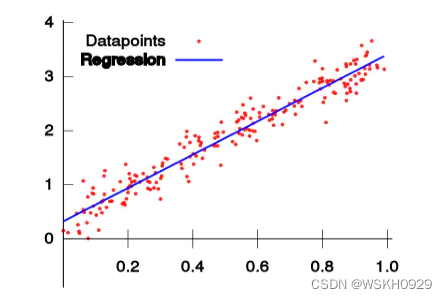
在这里插入图片描述

三、最小二乘法的公式

设拟合直线的公式为 $\bullet x+b$ ，

其中: 拟合直线的斜率为: $k=\frac{x y-n \bar{x} \bullet \bar{y}}{x^{2}-n(\bar{x})^{2}}$ ;

计算出斜率后，根据 $(\bar{x}, \bar{y})$ 和已经确定的斜率 $\mathrm{k}_{r}$ 利用待定系数法求出截距 $\mathrm{b}$ 。

四、Java代码实现最小二乘法

/*
**  Create by: WSKHDate:2022-01-08Time:19:38
*/
public class LeastSquaresRegression {double[] xData;double[] yData;public static void main(String[] args) {double[] xData = new double[]{1, 2, 3, 4,5,6,7,8,9,10,11,12};double[] yData = new double[]{4200,4300,4000,4400,5000,4700,5300,4900,5400,5700,6300,6000};double[] preX = {13,14,15,16,17,18,19,20,21,22,23,24};new LeastSquaresRegression(xData, yData).predict(preX);}public void predict(double[] preX) {// 计算nint n = xData.length;System.out.println("n = " + n);// 计算x，y，xy，x²的总和double totalX = 0d;double totalY = 0d;double totalXY = 0d;double totalX2 = 0d;for (int i = 0; i < xData.length; i++) {totalX += xData[i];totalY += yData[i];totalXY += xData[i] * yData[i];totalX2 += xData[i] * xData[i];}System.out.println("totalX = " + totalX);System.out.println("totalY = " + totalY);System.out.println("totalXY = " + totalXY);System.out.println("totalX2 = " + totalX2);// 计算x均值double meanX = totalX / n;System.out.println("meanX = " + meanX);// 计算y均值double meanY = totalY / n;System.out.println("meanY = " + meanY);// 计算斜率bdouble b = (totalXY - n * meanX * meanY) / (totalX2 - n * meanX * meanX);System.out.println("b = " + b);// 计算截距adouble a = meanY - b * meanX;System.out.println("a = " + a);// 线性方程System.out.printf("线性方程为: y = %.2f + %.2fx\n", a, b);// 预测for (double x : preX) {System.out.printf("x 为%.2f时，预测y值为：%.2f\n", x, a+b*x);}}public LeastSquaresRegression(double[] xData, double[] yData) {this.xData = xData;this.yData = yData;}
}

五、输出预测结果

n = 12
totalX = 78.0
totalY = 60200.0
totalXY = 418800.0
totalX2 = 650.0
meanX = 6.5
meanY = 5016.666666666667
b = 192.30769230769232
a = 3766.666666666667
线性方程为: y = 3766.67 + 192.31x
x 为13.00时，预测y值为：6266.67
x 为14.00时，预测y值为：6458.97
x 为15.00时，预测y值为：6651.28
x 为16.00时，预测y值为：6843.59
x 为17.00时，预测y值为：7035.90
x 为18.00时，预测y值为：7228.21
x 为19.00时，预测y值为：7420.51
x 为20.00时，预测y值为：7612.82
x 为21.00时，预测y值为：7805.13
x 为22.00时，预测y值为：7997.44
x 为23.00时，预测y值为：8189.74
x 为24.00时，预测y值为：8382.05