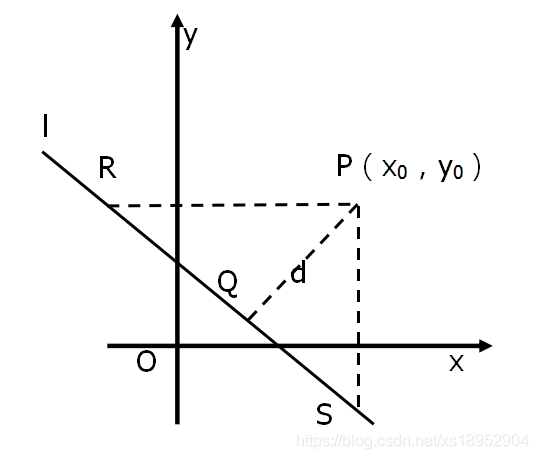
空间直线方程及两直线的夹角
1.空间直线的一般方程

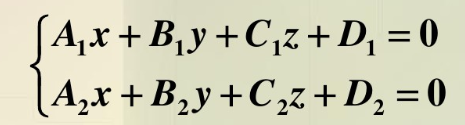
方向向量
与一直直线平行的非零向量
求法参照2.对称式方程
2.空间直线的点向式(对称式)方程
求的是平面

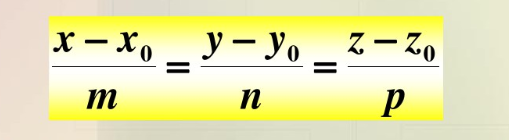
特殊情况


3.空间直线的参数方程(引入参数t)
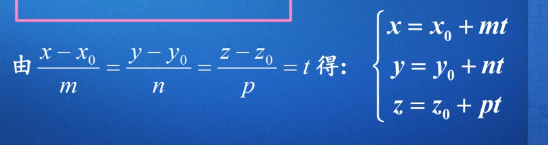
两直线的夹角(锐角)
是指的其方向向量的夹角

用向量夹角的公式

两直线相互垂直和平行的充分必要条件

垂直是向量数量积为0
平行时对应的方向向量成比例
直线与平面夹角
注意与直线与直线的夹角不一样
直线与直线的夹角是cos
直线与平面的夹角是sin

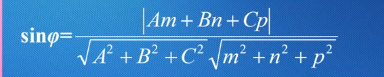
直线与平面垂直和平行的充分必要条件
主要考虑的是直线与平面的法向量关系

平面束
定义:过一条直线的所有的直线集合
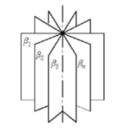

例子
与两平面交线平行的直线

直线与平面的交点