点到直线的距离公式推导
本文地址:blog.lucien.ink/archives/495
摘自 点到直线距离公式的几种推导 - 三横先生的文章 - 知乎 的三角形面积法,稍作修改并更正书写错误。
起因
今天在 PPT 里看到一个点到超平面的距离公式 d = 1 ∥ w ∥ ∣ w ⋅ x 0 + b ∣ d = \frac{ 1 }{ \left\| \boldsymbol w \right\| }| \boldsymbol w \cdot \boldsymbol x_0 + \boldsymbol b | d=∥w∥1∣w⋅x0+b∣,看了半天没看懂为什么这样算,遂去问学霸,答曰“平面情况下就是点到直线的距离公式”。
万分惭愧,我连初中数学都忘了。
三角形面积法
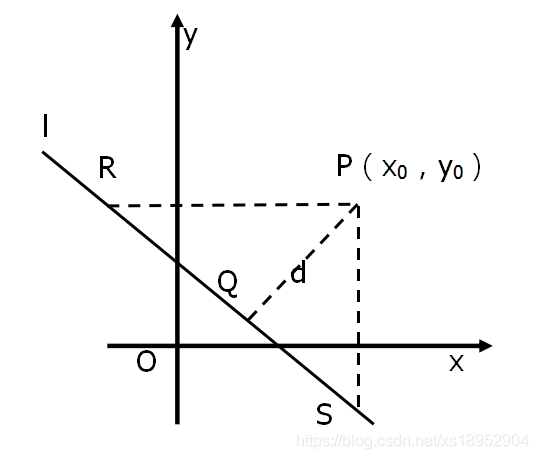
直线 l l l 方程为 A x + B y + C = 0 Ax + By + C = 0 Ax+By+C=0, A A A、 B B B 均不为 0 0 0,点 P ( x 0 , y 0 ) P(x_0, y_0) P(x0,y0),设点 P P P 到 l l l 的距离为 d d d。
设点 R ( x R , y 0 ) R(x_R, y_0) R(xR,y0),点 S ( x 0 , y S ) S(x_0, y_S) S(x0,yS)。
由 R , S R, S R,S 在直线 l l l 上,得到
A x R + B y 0 + C = 0 Ax_R + By_0 + C = 0 AxR+By0+C=0 A x 0 + B y S + C = 0 Ax_0 + By_S + C = 0 Ax0+ByS+C=0
所以
x R = − B y 0 − C A x_R = \frac{ -By_0 - C }{ A } xR=A−By0−C y S = − A x 0 − C B y_S = \frac{ -Ax_0 - C }{ B } yS=B−Ax0−C
即
∣ P R ∣ = ∣ x 0 − x R ∣ = ∣ x 0 − − B y 0 − C A ∣ = ∣ A x 0 + B y 0 + C A ∣ | PR | = | x_0 - x_R | = | x_0 - \frac{ -By_0 - C }{ A } | = | \frac{ Ax_0 + By_0 + C }{ A } | ∣PR∣=∣x0−xR∣=∣x0−A−By0−C∣=∣AAx0+By0+C∣ ∣ P S ∣ = ∣ y 0 − y S ∣ = ∣ y 0 − − A x 0 − C B ∣ = ∣ A x 0 + B y 0 + C B ∣ | PS | = | y_0 - y_S | = | y_0 - \frac{ -Ax_0 - C }{ B } | = | \frac{ Ax_0 + By_0 + C }{ B } | ∣PS∣=∣y0−yS∣=∣y0−B−Ax0−C∣=∣BAx0+By0+C∣
于是
∣ R S ∣ = P R 2 + P S 2 = A 2 + B 2 A B ⋅ ∣ A x 0 + B y 0 + C ∣ | RS | = \sqrt{ { PR }^2 + { PS }^2 } = \frac{ \sqrt{ A^2 + B^2 } }{ AB } \cdot | Ax_0 + By_0 + C | ∣RS∣=PR2+PS2=ABA2+B2⋅∣Ax0+By0+C∣
由 Δ P S R \Delta_{PSR} ΔPSR 得
d ⋅ ∣ R S ∣ = ∣ P R ∣ ⋅ ∣ P S ∣ d \cdot | RS | = | PR | \cdot | PS | d⋅∣RS∣=∣PR∣⋅∣PS∣
即
d = ∣ P R ∣ ⋅ ∣ P S ∣ ∣ R S ∣ = ∣ A x 0 + B y 0 + C A ∣ ⋅ ∣ A x 0 + B y 0 + C B ∣ A 2 + B 2 A B ⋅ ∣ A x 0 + B y 0 + C ∣ = ∣ A x 0 + B y 0 + C ∣ A 2 + B 2 d = \frac{ | PR | \cdot | PS | }{ | RS | } = \frac{ | \frac{ Ax_0 + By_0 + C }{ A } | \cdot | \frac{ Ax_0 + By_0 + C }{ B } | }{ \frac{ \sqrt{ A^2 + B^2 } }{ AB } \cdot | Ax_0 + By_0 + C | } = \frac{ | Ax_0 + By_0 + C | }{ \sqrt{ A^2 + B^2 } } d=∣RS∣∣PR∣⋅∣PS∣=ABA2+B2⋅∣Ax0+By0+C∣∣AAx0+By0+C∣⋅∣BAx0+By0+C∣=A2+B2∣Ax0+By0+C∣
另一种形式
设函数 f ( x , y ) = A x + B y + C f(x, y) = Ax + By + C f(x,y)=Ax+By+C,直线 l : A x + B y + C = 0 l: Ax + By + C = 0 l:Ax+By+C=0 的法向量为 v ( A , B ) \boldsymbol v(A, B) v(A,B)。
则点 P ( x 0 , y 0 ) P(x_0, y_0) P(x0,y0) 到直线 l l l 的距离 d d d 为
d = ∣ A x 0 + B y 0 + C ∣ A 2 + B 2 = f ( x 0 , y 0 ) ∥ v ∥ d = \frac{ | Ax_0 + By_0 + C | }{ \sqrt{ A^2 + B^2 } } = \frac{ f(x_0, y_0) }{ \left\| \boldsymbol v \right\| } d=A2+B2∣Ax0+By0+C∣=∥v∥f(x0,y0)
注: ∥ v ∥ \left\| \boldsymbol v \right\| ∥v∥ 为向量 v \boldsymbol v v 的 2-范数