LRU和LFU的区别

article/2025/10/17 0:53:33

对于web开发而言，缓存必不可少，也是提高性能最常用的方式。无论是浏览器缓存(如果是chrome浏览器，可以通过chrome:://cache查看)，还是服务端的缓存(通过memcached或者redis等内存数据库)。缓存不仅可以加速用户的访问，同时也可以降低服务器的负载和压力。那么，了解常见的缓存淘汰算法的策略和原理就显得特别重要。

常见的缓存算法

LRU (Least recently used) 最近最少使用，如果数据最近被访问过，那么将来被访问的几率也更高。
LFU (Least frequently used) 最不经常使用，如果一个数据在最近一段时间内使用次数很少，那么在将来一段时间内被使用的可能性也很小。
FIFO (Fist in first out) 先进先出，如果一个数据最先进入缓存中，则应该最早淘汰掉。

LRU缓存

像浏览器的缓存策略、memcached的缓存策略都是使用LRU这个算法，LRU算法会将近期最不会访问的数据淘汰掉。LRU如此流行的原因是实现比较简单，而且对于实际问题也很实用，良好的运行时性能，命中率较高。下面谈谈如何实现LRU缓存：

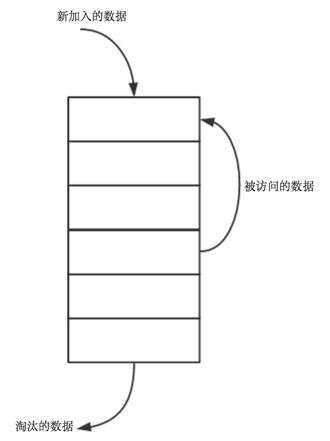
新数据插入到链表头部
每当缓存命中（即缓存数据被访问），则将数据移到链表头部
当链表满的时候，将链表尾部的数据丢弃

LRU Cache具备的操作：

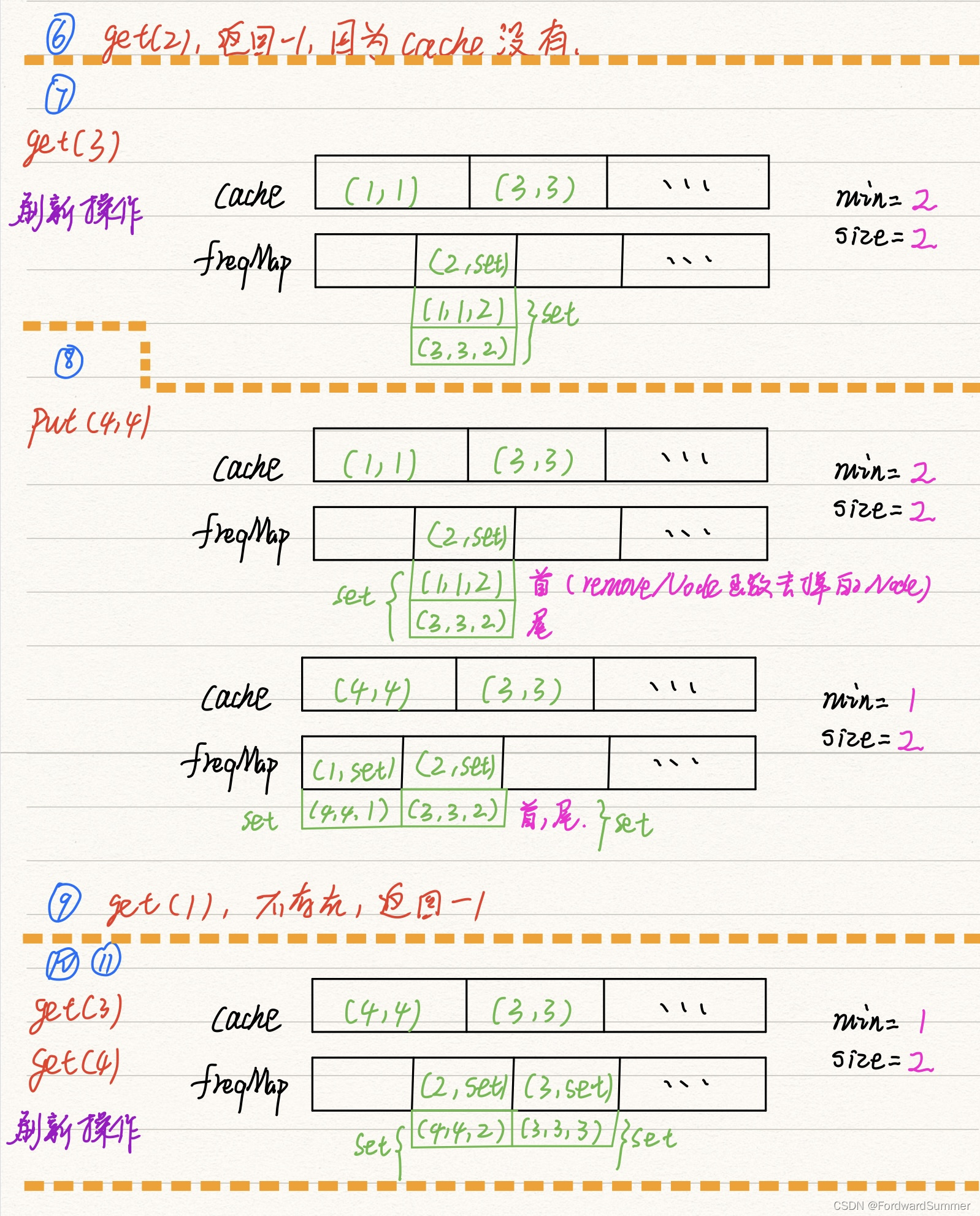
set(key,value)：如果key在hashmap中存在，则先重置对应的value值，然后获取对应的节点cur，将cur节点从链表删除，并移动到链表的头部；若果key在hashmap不存在，则新建一个节点，并将节点放到链表的头部。当Cache存满的时候，将链表最后一个节点删除即可。
get(key)：如果key在hashmap中存在，则把对应的节点放到链表头部，并返回对应的value值；如果不存在，则返回-1。

LRU的c++实现

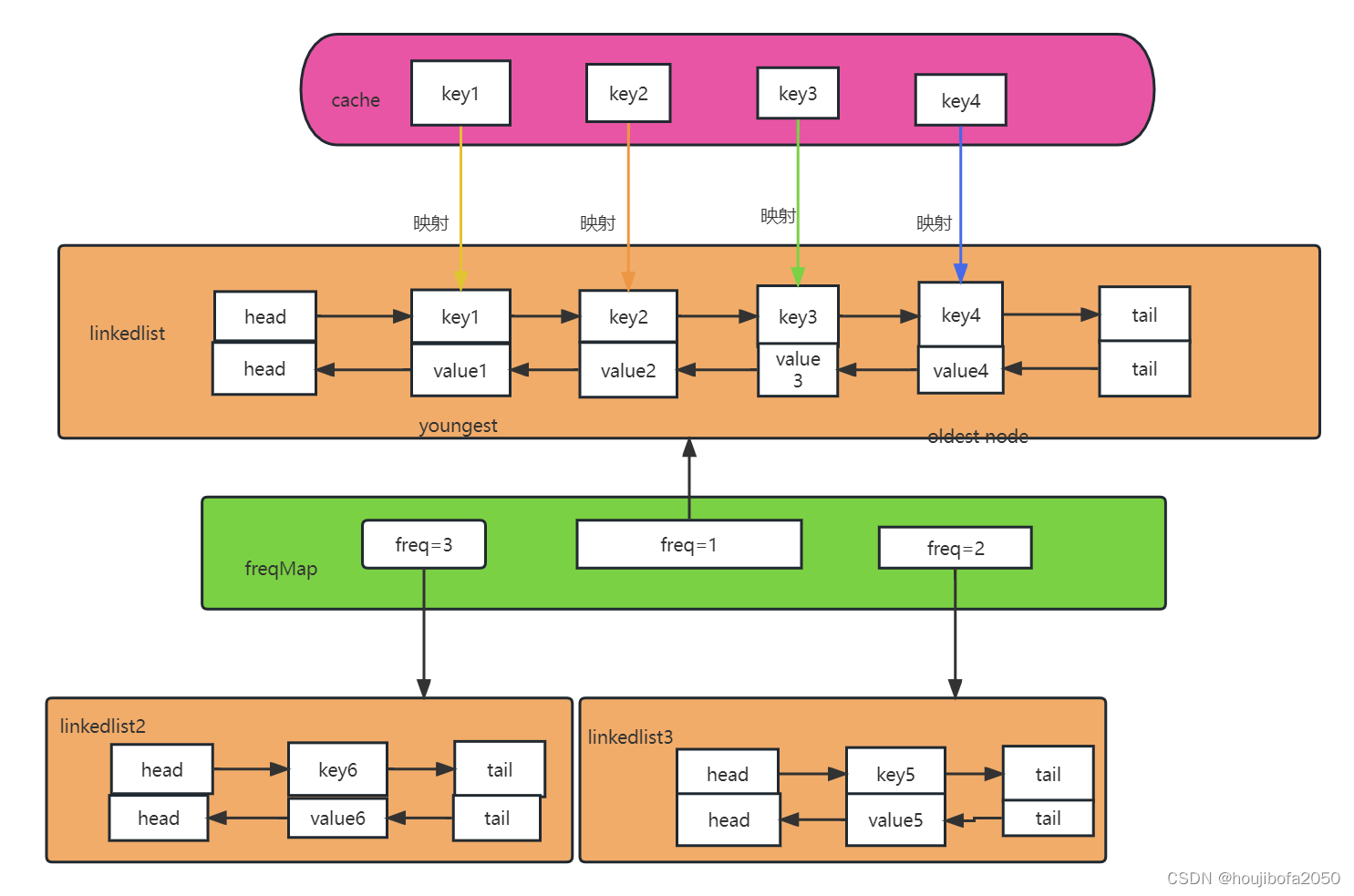
LRU实现采用双向链表 + Map 来进行实现。这里采用双向链表的原因是：如果采用普通的单链表，则删除节点的时候需要从表头开始遍历查找，效率为O(n)，采用双向链表可以直接改变节点的前驱的指针指向进行删除达到O(1)的效率。使用Map来保存节点的key、value值便于能在O(logN)的时间查找元素,对应get操作。

双链表节点的定义：

struct CacheNode {int key;      // 键int value;    // 值CacheNode *pre, *next;  // 节点的前驱、后继指针CacheNode(int k, int v) : key(k), value(v), pre(NULL), next(NULL) {}
};

对于LRUCache这个类而言，构造函数需要指定容量大小

LRUCache(int capacity)
{size = capacity;      // 容量head = NULL;          // 链表头指针tail = NULL;          // 链表尾指针
}

双链表的节点删除操作：

void remove(CacheNode *node)
{if (node -> pre != NULL){node -> pre -> next = node -> next;}else{head = node -> next;}if (node -> next != NULL){node -> next -> pre = node -> pre;}else{tail = node -> pre;}
}

将节点插入到头部的操作：

void setHead(CacheNode *node)
{node -> next = head;node -> pre = NULL;if (head != NULL){head -> pre = node;}head = node;if (tail == NULL){tail = head;}
}

get(key)操作的实现比较简单，直接通过判断Map是否含有key值即可，如果查找到key，则返回对应的value，否则返回-1;

int get(int key)
{map<int, CacheNode *>::iterator it = mp.find(key);if (it != mp.end()){CacheNode *node = it -> second;remove(node);setHead(node);return node -> value;}else{return -1;}
}

set(key, value)操作需要分情况判断。如果当前的key值对应的节点已经存在，则将这个节点取出来，并且删除节点所处的原有的位置，并在头部插入该节点；如果节点不存在节点中，这个时候需要在链表的头部插入新节点，插入新节点可能导致容量溢出，如果出现溢出的情况，则需要删除链表尾部的节点。

void set(int key, int value)
{map<int, CacheNode *>::iterator it = mp.find(key);if (it != mp.end()){CacheNode *node = it -> second;node -> value = value;remove(node);setHead(node);}else{CacheNode *newNode = new CacheNode(key, value);if (mp.size() >= size){map<int, CacheNode *>::iterator iter = mp.find(tail -> key);remove(tail);mp.erase(iter);}setHead(newNode);mp[key] = newNode;}
}

至此，LRU算法的实现操作就完成了，完整的源码参考：https://github.com/cpselvis/leetcode/blob/master/solution146.cpp

以上原文链接：https://www.cnblogs.com/cpselvis/p/6272096.html

补充：

LRU和LFU的区别：

LRU是最近最少使用页面置换算法(Least Recently Used),也就是首先淘汰最长时间未被使用的页面!

LFU是最近最不常用页面置换算法(Least Frequently Used),也就是淘汰一定时期内被访问次数最少的页!

比如,第二种方法的时期T为10分钟,如果每分钟进行一次调页,主存块为3,若所需页面走向为2 1 2 1 2 3 4

注意,当调页面4时会发生缺页中断

若按LRU算法,应换页面1(1页面最久未被使用) 但按LFU算法应换页面3(十分钟内,页面3只使用了一次)

可见LRU关键是看页面最后一次被使用到发生调度的时间长短,

而LFU关键是看一定时间段内页面被使用的频率!