0. 前置提要
本篇约为8650字,阅读完需要约40~60分钟。主要介绍页面置换算法,LRU和LFU的原理及其实现,对应leetcode140和460,如果能给个赞就更好了^-^。
1.从内存置换算法说起
计算机的运行的程序和数据保存在内存中,内存的空间是有限的,所运行的程序可能需要新的数据,而数据不在内存,在磁盘(硬盘)中。 CPU 访问的页面在物理内存时,便会产生一个缺页中断,请求操作系统将所缺页调入到物理内存。
对于要新加入内存的页面,需要一定的算法来确定把哪个页面剔除出去给新的要加进来的页面让位。所以,页面置换算法的功能是,当出现缺页异常,需调入新页面而内存已满时,选择被置换的物理页面,也就是说选择⼀个物理页面换出到磁盘,然后把需要访问的页面换入到物理页。
那其算法目标则是,尽可能减少页面的换入换出的次数,常见的页面置换算法有如下几种【1】:
最佳页面置换算法(OPT)
先进先出置换算法(FIFO)
最近最久未使用的置换算法(LRU)
时钟页面置换算法(Lock)
最不常用置换算法(LFU)
1.1 最佳页面置换算法(OPT)
最佳页面置换算法基本思路是,置换在「未来」最⻓时间不访问的页面。所以,该算法实现需要计算内存中每个逻辑页面的「下⼀次」访问时间,然后比较,选择未来最长时间不访问的页面。我们举个例⼦,假设⼀开始有 3 个空闲的物理页,然后有请求的页面序列,那它的置换过程如下图【图源自小林coding】:

在这个请求的页面序列中,缺页共发生了 7 次(空闲页换入 3 次 + 最优页面置换 4 次),页面置换共发生了 4 次。这很理想,但是实际系统中无法实现,因为程序访问页面时是动态的,我们是无法预知每个页面在「下⼀次」访问前的等待时间。所以,最佳页面置换算法作用是为了衡量你的算法的效率,你的算法效率越接近该算法的效率,那么说明你的算法是高效的。
1.2 先进先出置换算法(FIFO)
既然我们⽆法预知页面在下⼀次访问前所需的等待时间,那我们可以选择在内存驻留时间而后南昌的页面进行中置换,这个就是「先进先出置换」算法的思想。还是以前⾯的请求的⻚⾯序列作为例子,假设使用先进先出出置换算法,则过程如下图:

在这个请求的页面序列中,缺页共发生了 10 次,页面置换共发⽣了 7 次,跟最佳页面置换算法比较起来,性能明显差了很多。
1.3 最近最久未使用的置换算法(LRU)
最近最久未使用(LRU)的置换算法的基本思路是,发生缺页时,选择最长时间没有被访问的页面进行置 换,也就是说,该算法假设已经很久没有使用的页面很有可能在未来较长的⼀段时间内仍然不会被使用。 这种算法近似最优置换算法,最优置换算法是通过「未来」的使用情况来推测要淘汰的页面,而 LRU 则是 通过「历史」的使用情况来推测要淘汰的页面。 还是以前⾯的请求的页面序列作为例子,假设使用最近最久未使用的置换算法,则过程如下图:

在这个请求的页面序列中,缺页共发⽣了 9 次,页面置换共发⽣了 6 次,跟先进先出置换算法⽐较起 来,性能提高了⼀些。虽然 LRU 在理论上是可以实现的,但代价很高。为了完全实现 LRU,需要在内存中维护⼀个所有页面的 链表,最近最多使用的页面在表头,最近最少使用的页面在表尾。 困难的是,在每次访问内存时都必须要更新「整个链表」。在链表中找到⼀个页面,删除它,然后把它移 动到表头是⼀个⾮常费时的操作。 所以,LRU 虽然看上去不错,但是由于开销比较大,实际应用中比较少使用。
1.4 时钟页面置换算法(Lock)
时钟页面置换算法就可以两者兼得,它跟 LRU 近似,又是对 FIFO 的⼀种改进。 该算法的思路是,把所有的页面都保存在⼀个类似钟面的「环形链表」中,⼀个表针指向最老的页面。 当发生缺页中断时,算法首先检查表针指向的页面: 如果它的访问位位是 0 就淘汰该页面,并把新的页面插入这个位置,然后把表针前移⼀个位置; 如果访问位是 1 就清除访问位,并把表针前移⼀个位置,重复这个过程直到找到了⼀个访问位为 0 的 页面为止;
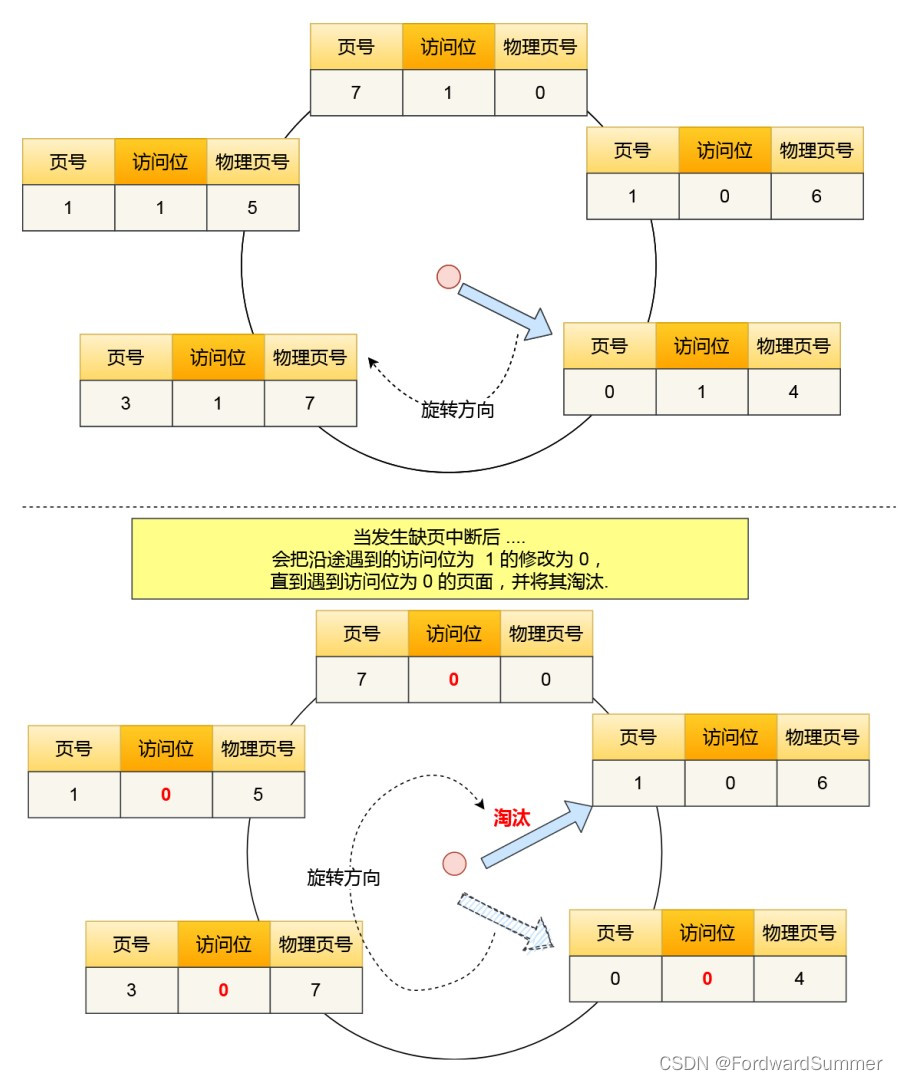
1.5 最不常用置换算法(LFU)
最不常用(LFU)算法,这名字听起来很调皮,但是它的意思不是指这个算法不常用,而是当发生缺页中 断时,选择「访问次数」最少的那个页面,并将其淘汰。 它的实现方式是,对每个页面设置⼀个「访问计数器」,每当⼀个页面被访问时,该页面的访问计数器就 累加 1。在发生缺页中断时,淘汰计数器值最小的那个页面。 看起来很简单,每个页面加⼀个计数器就可以实现了,但是在操作系统中实现的时候,我们需要考虑效率和硬件成本的。 要增加⼀个计数器来实现,这个硬件成本是比较高的,另外如果要对这个计数器查找哪个页面访问次数最 小,查找链表本身,如果链表长度很大,是非常耗时的,效率不高。 但还有个问题,LFU 算法只考虑了频率问题,没考虑时间的问题,比如有些页面在过去时间里访问的频率很高,但是现在已经没有访问了,而当前频繁访问的页面由于没有这些页面访问的次数高,在发生缺页中 断时,就会可能会误伤当前刚开始频繁访问,但访问次数还不高的页面。 那这个问题的解决的办法还是有的,可以定期减少访问的次数,比如当发生时间中断时,把过去时间访问 的页面的访问次数除以 2,也就说,随着时间的流失,以前的高访问次数的页面会慢慢减少,相当于加大 了被置换的概率。
2.LRU实现
2.1 总体思路
总体上,LRU的实现可以依据LinkedHashMap,依靠LinkedHashMap的特性,在最初添加的时候就是最近使用的。
LinkedHashMap继承自HashMap,它的多种操作都是建立在HashMap操作的基础上的。同HashMap不同的是,LinkedHashMap维护了一个Entry的双向链表,保证了插入的Entry中的顺序。这也是Linked的含义【3】。如果对LinkedHashMap还不太了解,可以参考【3】。
2.2 代码实现
class LRUCache {int cap;//容量LinkedHashMap<Integer, Integer> cache = new LinkedHashMap<>(); //首先定义的HashMappublic LRUCache(int capacity) { this.cap = capacity;//给容量赋值}public int get(int key) {if (!cache.containsKey(key)) {//查找key,不包含的话返回-1return -1;}makeRecently(key);// 将 key 变为最近使用return cache.get(key);}public void put(int key, int val) {if (cache.containsKey(key)) {//如果说包含的话,就更新// 修改 key 的值cache.put(key, val);// 将 key 变为最近使用makeRecently(key);return;}if (cache.size() >= this.cap) {//如果说容量大于预设容量// 链表头部就是最久未使用的 keyint oldestKey = cache.keySet().iterator().next();//取头部,然后扔掉cache.remove(oldestKey);}// 将新的 key 添加链表尾部cache.put(key, val);}private void makeRecently(int key) {int val = cache.get(key);// 删除 key,重新插入到队尾cache.remove(key);//删除,删除头部cache.put(key, val);//队尾就是最新的}
}2.3 案例解析
输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
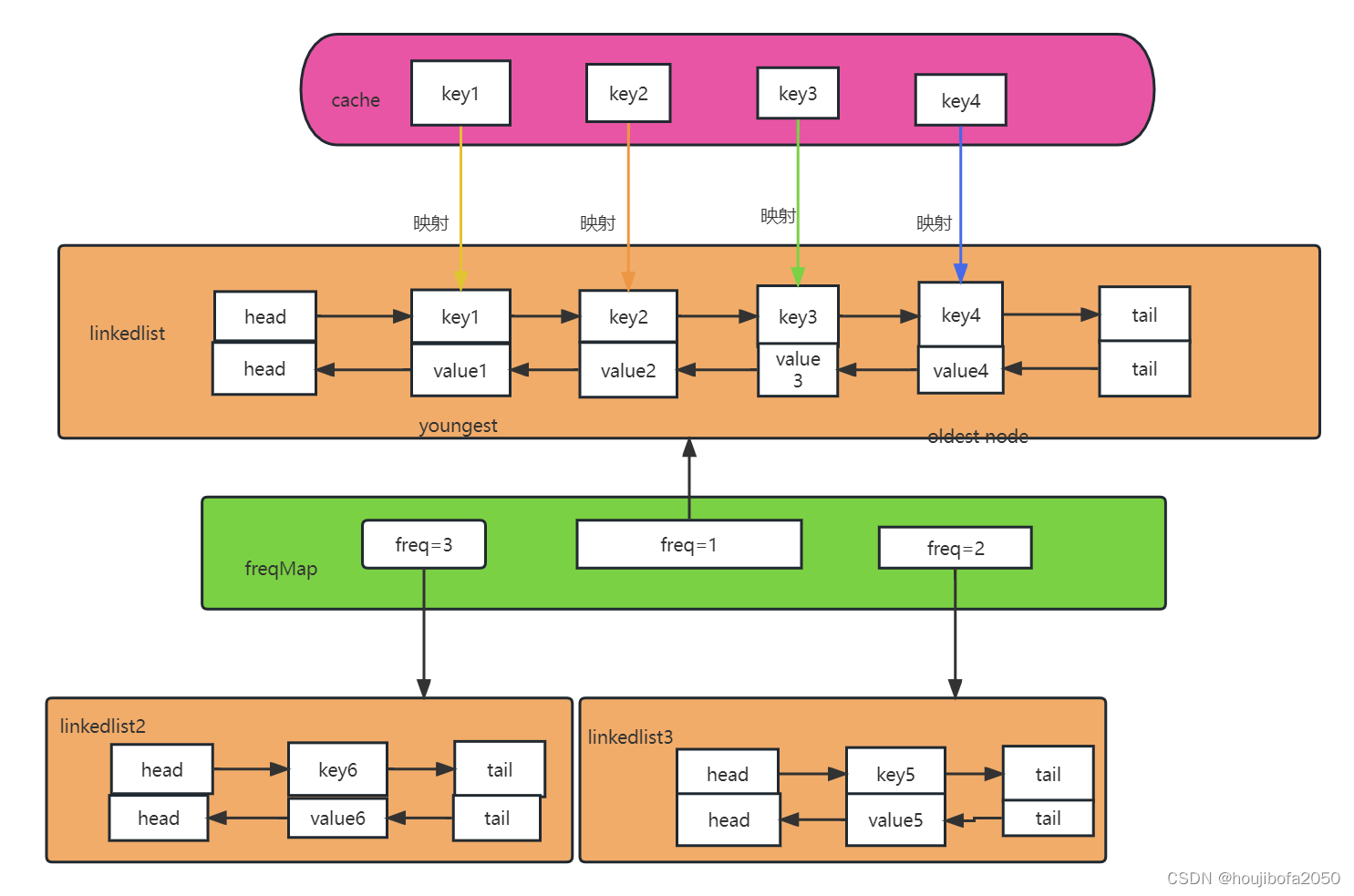
直接上图

3.LFU实现
3.1 总体思路
总体上,LFU的实现基于HashMap和LinkedHashMap。由于要知道频率这一关键参数,那么LFU比LFU要多一层逻辑,也就是记录频率的外层和记录key和LinkedHashMap的里层,LFU本身实现要比LRU多一层逻辑,也更麻烦,所以在这里把步骤拆分,看3.3里更容易理解代码。
3.2 代码实现
class LFUCache {int capacity;//key是本身的key,value是NodeHashMap<Integer,Node> cache = new HashMap<>();//key是频率,value是一个一个NodeHashMap<Integer,LinkedHashSet<Node>> freqMap = new HashMap<>();int min;//存储最小值int size;//记录已经存了多少值public LFUCache(int capacity) {this.capacity = capacity;}public int get(int key) {Node node = cache.get(key);//得到该nodeif(node == null){//node可能为空进行判断return -1;}freqInc(node);//因为调用了一次,所以堆频率进行更新,也就是去更新freqMapreturn node.value;//返回node中value的值}public void put(int key, int value) {if(capacity == 0){//当容量为0时不能添加return;}Node node = cache.get(key);//如果获得的node为空证明需要新添加if(node != null){//如果获得的node不为空证明需要更新,更新调用freInc函数更新node.value = value;freqInc(node);}else{if(capacity == size){//如果满了要删除,删除就删除那个minNode deadNode = removeNode();;cache.remove(deadNode.key);size--;}Node newnode = new Node(key,value);cache.put(key,newnode);addNode(newnode);size++;}}public void freqInc(Node node){int freq = node.freq;LinkedHashSet<Node> set = freqMap.get(freq);set.remove(node);if(freq == min && set.size() == 0){//如果说freq频率是最小的 并且set的长度是0(去掉之后导致人家为0)min = freq +1;}node.freq++;//把对应的频率加一set = freqMap.get(node.freq);if(set == null){//如果是null则需要重新建立set = new LinkedHashSet<>();freqMap.put(node.freq,set);}set.add(node);}public void addNode(Node node){LinkedHashSet<Node> set = freqMap.get(1);if(set == null){set = new LinkedHashSet<>(); freqMap.put(1,set);}set.add(node);min = 1;} public Node removeNode(){LinkedHashSet<Node> set = freqMap.get(min);//得到最小值准备去掉Node deadNode = set.iterator().next();//用iterator遍历去掉第一个set.remove(deadNode);//去掉return deadNode;//返回去掉值}
}
//节点的数据结构有key,value和频率值
class Node{int key;int value;int freq = 1;public Node(){}public Node(int key, int value){this.value = value;this.key = key;}
}3.3 分步拆解
3.3.1 整体构成
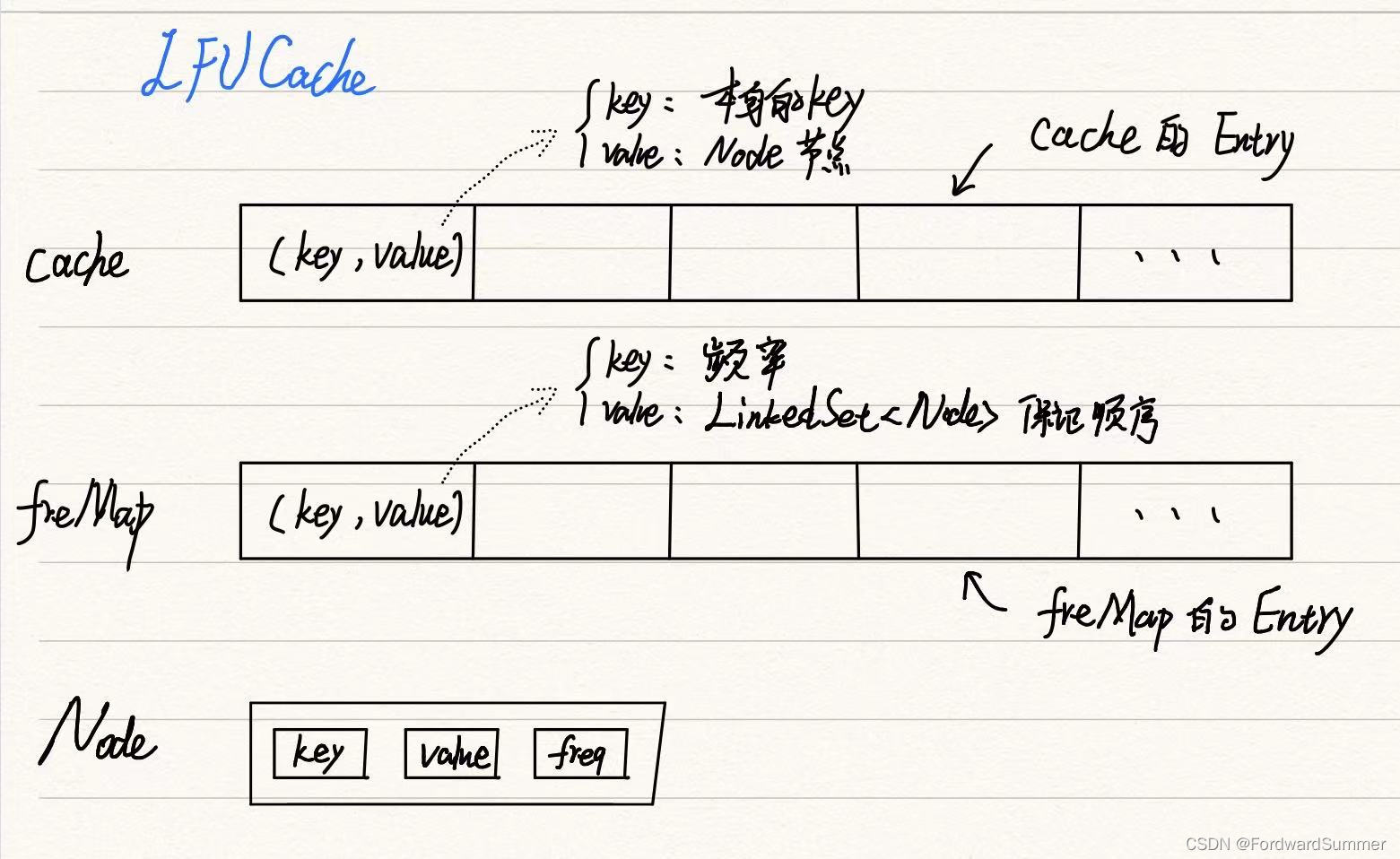
整体上,可以拆分为3个部分, 管频率的freMap,管key和value的cache,管一个数据节点具体值得Node。
3.3.2 Node构成
class Node{int key;int value;int freq = 1;public Node(){}public Node(int key, int value){this.value = value;this.key = key;}
}Node节点很好理解, 由key,value和频率freq构成。
3.3.3 初始化
int capacity;//key是本身的key,value是NodeHashMap<Integer,Node> cache = new HashMap<>();//key是频率,value是一个一个NodeHashMap<Integer,LinkedHashSet<Node>> freqMap = new HashMap<>();int min;//存储最小值int size;//记录已经存了多少值public LFUCache(int capacity) {this.capacity = capacity;}在初始化中,有额外的 min用来记录最小值,min值对应的LinkedHashSet意味着是使用频率最小的哪个值。当capacity满了时,就要删除那个min值对应的Node。size用来记录存了多少个值,capacity是用来正常初始化缓存的容量,当size==capacity时,证明满了,需要删除。
3.3.4 刷新函数freqInc
public void freqInc(Node node){int freq = node.freq;LinkedHashSet<Node> set = freqMap.get(freq);set.remove(node);if(freq == min && set.size() == 0){//如果说freq频率是最小的 并且set的长度是0(去掉之后导致人家为0)min = freq +1;}node.freq++;//把对应的频率加一set = freqMap.get(node.freq);if(set == null){//如果是null则需要重新建立set = new LinkedHashSet<>();freqMap.put(node.freq,set);}set.add(node);}在遇到get,put方法时,都要调用刷新函数,传入Node节点,进行刷新。那么在进行刷新的时候,一是要把本来的节点在freMap上的相应节点删除掉,二是要在相应的频率的位置上添加新的节点。在此期间需要判断是不是最小值的哪个节点,如果是需要进行额外的操作。对于频率加一的新节点,也要判断对应的频率位置上有没有数据,没有要建立新的LinkedHashSet。
3.3.5 put方法
public void put(int key, int value) {if(capacity == 0){//当容量为0时不能添加return;}Node node = cache.get(key);//如果获得的node为空证明需要新添加if(node != null){//如果获得的node不为空证明需要更新,更新调用freInc函数更新node.value = value;freqInc(node);}else{if(capacity == size){//如果满了要删除,删除就删除那个minNode deadNode = removeNode();;cache.remove(deadNode.key);size--;}Node newnode = new Node(key,value);cache.put(key,newnode);addNode(newnode);size++;}}在put时要注意节点本身是不是存在的,存在则更新,更新调用freqInc函数。不存在则新建立节点,此时注意是否为满,为满则删除频率为min的哪个节点。在挂载新的节点后,也是要在freqMap进行更新的。若不存在这个节点,那么频率设为1,已存在则直接添加。
3.3.6 addNode方法
public void addNode(Node node){LinkedHashSet<Node> set = freqMap.get(1);if(set == null){set = new LinkedHashSet<>(); freqMap.put(1,set);}set.add(node);min = 1;} 涉及到addNode都是新节点的添加,因为不是新节点则在put方法中的 if(node != null)被验证过了。此时就分两种情况,频率为1的节点上有没有值,有的化直接把Node节点挂载到下面,没有则新建一个LinkedHashSet<>()。
3.3.7 removeNode方法
public Node removeNode(){LinkedHashSet<Node> set = freqMap.get(min);//得到最小值准备去掉Node deadNode = set.iterator().next();//用iterator遍历去掉第一个set.remove(deadNode);//去掉return deadNode;//返回去掉值}当容量满了要添加新的Node进来时,需要把旧的去除,也就是使用频率最低的哪个,也就是min值对应的节点。但此时可能有多个节点都是使用最小值,也就是freqMap对应频率为min的Node有多个,去除那个最旧的(第一个,可参考2.3)。
3.3.8 get方法
public int get(int key) {Node node = cache.get(key);//得到该nodeif(node == null){//node可能为空进行判断return -1;}freqInc(node);//因为调用了一次,所以堆频率进行更新,也就是去更新freqMapreturn node.value;//返回node中value的值}从cache中判断是否有该值,因为调用了一次,所以要进行刷新操作。
3.4 案例解析
输入:
["LFUCache", "put", "put", "get", "put", "get", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [3], [4, 4], [1], [3], [4]]
输出:
[null, null, null, 1, null, -1, 3, null, -1, 3, 4]
解释:
// cnt(x) = 键 x 的使用计数
// cache=[] 将显示最后一次使用的顺序(最左边的元素是最近的)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=[1,_], cnt(1)=1
lfu.put(2, 2); // cache=[2,1], cnt(2)=1, cnt(1)=1
lfu.get(1); // 返回 1
// cache=[1,2], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 去除键 2 ,因为 cnt(2)=1 ,使用计数最小
// cache=[3,1], cnt(3)=1, cnt(1)=2
lfu.get(2); // 返回 -1(未找到)
lfu.get(3); // 返回 3
// cache=[3,1], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // 去除键 1 ,1 和 3 的 cnt 相同,但 1 最久未使用
// cache=[4,3], cnt(4)=1, cnt(3)=2
lfu.get(1); // 返回 -1(未找到)
lfu.get(3); // 返回 3
// cache=[3,4], cnt(4)=1, cnt(3)=3
lfu.get(4); // 返回 4
// cache=[3,4], cnt(4)=2, cnt(3)=3
直接上图

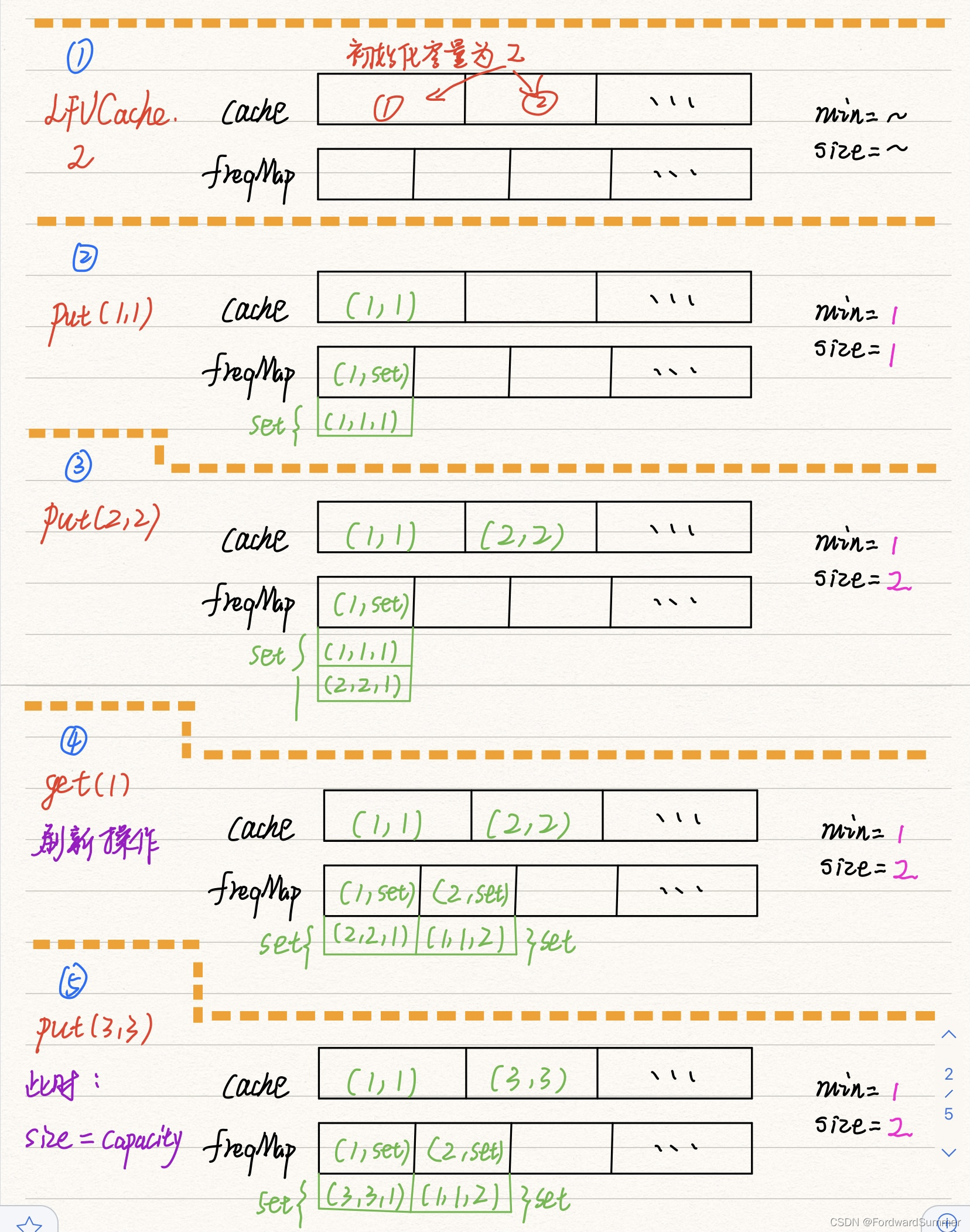
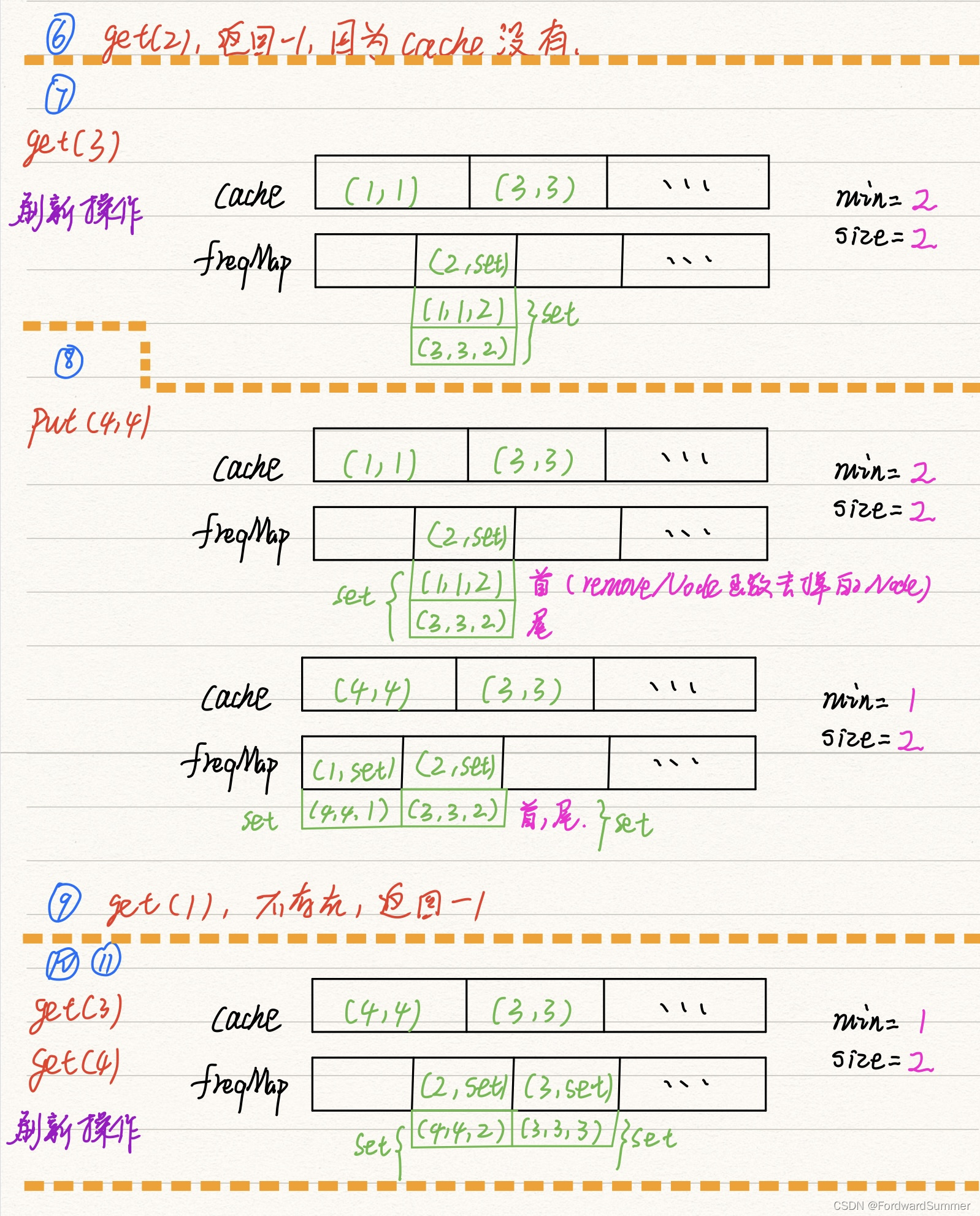
参考来源【1】小林coding 图解系统 内存页面置换算法
【2】leetcode labuladong LRU 策略详解和实现
【3】CSDN 求offer的菜鸡 超详细LinkedHashMap解析
【4】leetcode Sweetiee Java 13ms 双100% 双向链表 多解法超全😂