什么是范数,及其对应的 "曼哈顿距离"、"欧式距离"、"闵氏距离"、"切比雪夫距离"
- 一、什么是范数
- 二、欧式距离(对应L2范数)
- 三、曼哈顿距离(对应L1范数)
- 三、闵氏距离(对应Lp范数)
- 四、切比雪夫距离(对应L∞范数)
一、什么是范数
我们知道距离的定义是一个宽泛的概念,只要满足非负、自反、三角不等式就可以称之为距离。范数是一种强化了的距离概念,它在定义上比距离多了一条数乘的运算法则。有时候为了便于理解,我们可以把范数当作距离来理解。
在数学上,范数包括向量范数和矩阵范数,向量范数表征向量空间中向量的大小,矩阵范数表征矩阵引起变化的大小。一种非严密的解释就是,对应向量范数,向量空间中的向量都是有大小的,这个大小如何度量,就是用范数来度量的,不同的范数都可以来度量这个大小,就好比米和尺都可以来度量远近一样;对于矩阵范数,学过线性代数,我们知道,通过运算,可以将向量X变化为B,矩阵范数就是来度量这个变化大小的。
向量的范数定义:向量的范数是一个函数||x||,满足非负性||x|| >= 0,齐次性||cx|| = |c| ||x|| ,三角不等式||x+y|| <= ||x|| + ||y||。
常用的向量的范数:
-
L1范数(曼哈顿距离): ||x|| 为x向量各个元素绝对值之和。

-
L2范数(欧式距离): ||x||为x向量各个元素平方和的1/2次方(L2范数又称Euclidean范数或者Frobenius范数)。

-
Lp范数(闵氏距离): ||x||为x向量各个元素绝对值p次方和的1/p次方。

-
L∞范数(切比雪夫距离): ||x||为x向量各个元素绝对值最大那个元素的绝对值。

二、欧式距离(对应L2范数)
欧几里得度量(euclidean metric)(也称欧氏距离)是一个通常采用的距离定义,指在N维空间中两个点之间的真实距离,或者向量的自然长度(即该点到原点的距离)。在二维和三维空间中的欧氏距离就是两点之间的实际距离。
三、曼哈顿距离(对应L1范数)
在 “欧几里得空间” 的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。
例如在平面上,坐标(x11, x12)的向量 x1 与坐标(y11, y12)的向量 y1 的曼哈顿距离为:|x11 - y11| + |x12 - y12|,要注意的是:曼哈顿距离依赖座标系统的转度,而非系统在座标轴上的平移或映射。【x11表示第一行第一个元素,例如 x = [[1,2,3],[4,5,6]] ,x11为1,x12为2,x21为4】
顾名思义,在曼哈顿街区要从一个十字路口开车到另一个十字路口,驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”(City Block distance)。

下图中绿线代表欧氏距离。红、蓝、黄线代表曼哈顿距离(这三条折线的长度是相等的)。

三、闵氏距离(对应Lp范数)
闵氏距离又叫做闵可夫斯基距离,是欧氏空间中的一种测度,被看做是欧氏距离的一种推广,欧氏距离是闵可夫斯基距离的一种特殊情况。
四、切比雪夫距离(对应L∞范数)
当p = ∞时,即为切比雪夫距离:各坐标轴数据差的最大值:

转载与参考:
https://blog.csdn.net/zhaomengszu/article/details/77855167
https://blog.csdn.net/qq_27586341/article/details/107220041



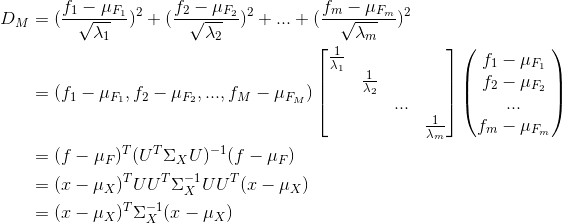





![[机器学习-概念] 什么是欧式距离、标准化欧式距离、马氏距离、余弦距离](https://img-blog.csdnimg.cn/20200703235519658.png)