一般在机器学习模型中会涉及到衡量两个样本间的距离,如聚类、KNN,K-means等,使用的距离为欧式距离。其实,除了欧氏距离之外,还有很多的距离计算标准,本文主要介绍欧氏距离和马氏距离。
欧氏距离
最常见的两点之间或多点之间的距离表示法,又称之为欧几里得度量,它定义于欧几里得空间中,如点 x = ( x 1 , … , x n ) x = (x_1,…,x_n) x=(x1,…,xn) 和 y = ( y 1 , … , y n ) y = (y_1,…,y_n) y=(y1,…,yn) 之间的距离为:
d ( x , y ) = ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 + . . . + ( x n − y n ) 2 = ∑ i = 1 n ( x i − y i ) 2 d(x,y) = \sqrt{(x_1-y_1)^2+(x_2-y_2)^2+...+(x_n-y_n)^2} = \sqrt{\sum_{i=1}^{n}(x_i-y_i)^2} d(x,y)=(x1−y1)2+(x2−y2)2+...+(xn−yn)2=i=1∑n(xi−yi)2
-
二维平面上两点a(x1,y1)与b(x2,y2)间的欧氏距离:
d 12 = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 d_{12} = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2} d12=(x1−x2)2+(y1−y2)2 -
两个n维向量 a ( x 11 , x 12 , … , x 1 n ) a(x_{11},x_{12},…,x_{1n}) a(x11,x12,…,x1n)与 b ( x 21 , x 22 , … , x 2 n ) b(x_{21},x_{22},…,x_{2n}) b(x21,x22,…,x2n)间的欧氏距离:
d 12 = ∑ k = 1 n ( x 1 k − x 2 k ) 2 d_{12} = \sqrt{\sum_{k=1}^{n}(x_{1k}-x_{2k})^2} d12=k=1∑n(x1k−x2k)2
马氏距离
在介绍马氏距离之前,我们先来看如下几个概念:
-
方差:方差是标准差的平方,而标准差的意义是数据集中各个点到均值点距离的平均值。反应的是数据的离散程度。
-
协方差: 标准差与方差是描述一维数据的,当存在多维数据时,我们通常需要知道每个维数的变量中间是否存在关联。协方差就是衡量多维数据集中,变量之间相关性的统计量。比如说,一个人的身高与他的体重的关系,这就需要用协方差来衡量。如果两个变量之间的协方差为正值,则这两个变量之间存在正相关,若为负值,则为负相关。
-
协方差矩阵: 当变量多了,超过两个变量了。那么,就用协方差矩阵来衡量这么多变量之间的相关性。假设 X X X 是以 n n n个随机变数(其中的每个随机变数是也是一个向量,当然是一个行向量)组成的列向量:
X = [ X 1 X 2 ⋮ X n ] X = \begin{bmatrix} X_1 \\ X_2 \\ \vdots \\ X_n \end{bmatrix} X=⎣⎢⎢⎢⎡X1X2⋮Xn⎦⎥⎥⎥⎤
其中, μ i μ_i μi是第i个元素的期望值,即 μ i = E ( X i ) μ_i=E(X_i) μi=E(Xi)。协方差矩阵的第 i , j i,j i,j项(第 i , j i,j i,j项是一个协方差)被定义为如下形式:
∑ i j = c o v ( X i , X j = E [ ( X i − μ i ) ( X j − μ j ) ] ) \sum_{ij} = cov(X_i,X_j = E[(X_i-\mu_i)(X_j-\mu_j)]) ij∑=cov(Xi,Xj=E[(Xi−μi)(Xj−μj)])
即:
∑ = [ E [ ( X 1 − μ 1 ) ( X 1 − μ 1 ) ] ) E [ ( X 1 − μ 1 ) ( X 2 − μ 2 ) ] ) ⋯ E [ ( X 1 − μ 1 ) ( X n − μ n ) ] ) E [ ( X 2 − μ 2 ) ( X 1 − μ 1 ) ] ) E [ ( X 2 − μ 2 ) ( X 2 − μ 2 ) ] ) ⋯ E [ ( X 2 − μ 2 ) ( X n − μ n ) ] ) ⋮ ⋮ ⋱ ⋮ E [ ( X n − μ n ) ( X 1 − μ 1 ) ] ) E [ ( X n − μ n ) ( X 2 − μ 2 ) ] ) ⋯ E [ ( X n − μ n ) ( X n − μ n ) ] ) ] \sum = \begin{bmatrix} E[(X_1-\mu_1)(X_1-\mu_1)]) & E[(X_1-\mu_1)(X_2-\mu_2)]) & \cdots & E[(X_1-\mu_1)(X_n-\mu_n)]) \\ E[(X_2-\mu_2)(X_1-\mu_1)]) & E[(X_2-\mu_2)(X_2-\mu_2)]) & \cdots & E[(X_2-\mu_2)(X_n-\mu_n)]) \\ \vdots & \vdots & \ddots & \vdots \\ E[(X_n-\mu_n)(X_1-\mu_1)]) & E[(X_n-\mu_n)(X_2-\mu_2)]) & \cdots & E[(X_n-\mu_n)(X_n-\mu_n)]) \end{bmatrix} ∑=⎣⎢⎢⎢⎡E[(X1−μ1)(X1−μ1)])E[(X2−μ2)(X1−μ1)])⋮E[(Xn−μn)(X1−μ1)])E[(X1−μ1)(X2−μ2)])E[(X2−μ2)(X2−μ2)])⋮E[(Xn−μn)(X2−μ2)])⋯⋯⋱⋯E[(X1−μ1)(Xn−μn)])E[(X2−μ2)(Xn−μn)])⋮E[(Xn−μn)(Xn−μn)])⎦⎥⎥⎥⎤
矩阵中的第 ( i , j ) (i,j) (i,j) 个元素是 X i X_i Xi 与 X j X_j Xj 的协方差。
马氏距离的定义:
马氏距离(Mahalanobis Distance)是由马哈拉诺比斯(P. C. Mahalanobis)提出的,表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的)并且是尺度无关的(scale-invariant),即独立于测量尺度。
对于一个均值为 μ = ( μ 1 , μ 2 , μ 3 , . . . , μ p ) T μ=(μ_1,μ_2,μ_3,...,μ_p)^T μ=(μ1,μ2,μ3,...,μp)T,协方差矩阵为 S S S的多变量 x = ( x 1 , x 2 , x 3 , . . . , x p ) T x=(x_1,x_2,x_3,...,x_p)^T x=(x1,x2,x3,...,xp)T,其马氏距离为:
D M ( x ) = ( x − μ ) T S − 1 ( x − μ ) D_M(x) = \sqrt{(x-\mu)^T {S}^{-1}(x-\mu)} DM(x)=(x−μ)TS−1(x−μ)
我们可以发现如果 S − 1 S^{-1} S−1是单位阵的时候,马氏距离简化为欧氏距离。
那我们为什么要用马氏距离呢?
马氏距离有很多优点: 马氏距离不受量纲的影响,两点之间的马氏距离与原始数据的测量单位无关;由标准化数据和中心化数据(即原始数据与均值之差)计算出的二点之间的马氏距离相同。马氏距离还可以排除变量之间的相关性的干扰。
下面我们来看一个例子:
如果我们以厘米为单位来测量人的身高,以克(g)为单位测量人的体重。每个人被表示为一个两维向量,如一个人身高173cm,体重50000g,表示为(173,50000),根据身高体重的信息来判断体型的相似程度。
我们已知小明(160,60000);小王(160,59000);小李(170,60000)。根据常识可以知道小明和小王体型相似。但是如果根据欧几里得距离来判断,小明和小王的距离要远远大于小明和小李之间的距离,即小明和小李体型相似。这是因为不同特征的度量标准之间存在差异而导致判断出错。
以克(g)为单位测量人的体重,数据分布比较分散,即方差大,而以厘米为单位来测量人的身高,数据分布就相对集中,方差小。马氏距离的目的就是把方差归一化,使得特征之间的关系更加符合实际情况。
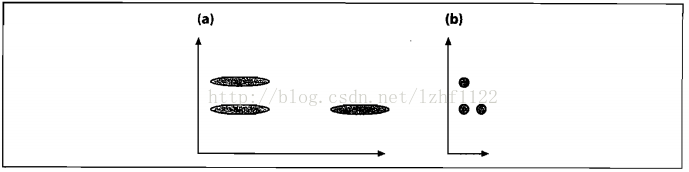
下图(a)展示了三个数据集的初始分布,看起来竖直方向上的那两个集合比较接近。在我们根据数据的协方差归一化空间之后,如图(b),实际上水平方向上的两个集合比较接近。
深入分析:
当求距离的时候,由于随机向量的每个分量之间量级不一样,比如说x1可能取值范围只有零点几,而x2有可能时而是2000,时而是3000,因此两个变量的离散度具有很大差异
马氏距离除以了一个方差矩阵,这就把各个分量之间的方差都除掉了,消除了量纲性,更加科学合理。
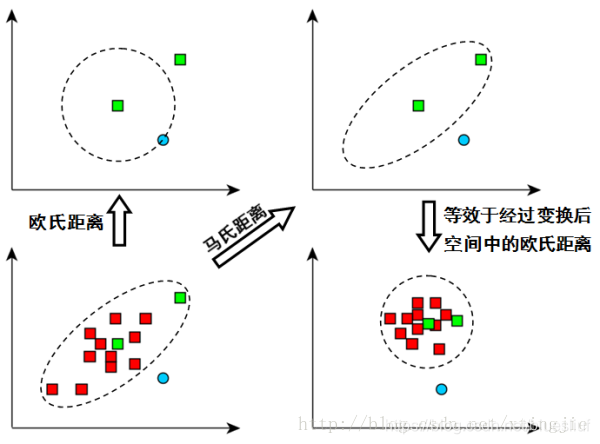
如上图,看左下方的图,比较中间那个绿色的和另外一个绿色的距离,以及中间绿色到蓝色的距离
如果不考虑数据的分布,就是直接计算欧式距离,那就是蓝色距离更近
但实际上需要考虑各分量的分布的,呈椭圆形分布
蓝色的在椭圆外,绿色的在椭圆内,因此绿色的实际上更近
马氏距离除以了协方差矩阵,实际上就是把右上角的图变成了右下角
参考资料:
马氏距离通俗理解




![[机器学习-概念] 什么是欧式距离、标准化欧式距离、马氏距离、余弦距离](https://img-blog.csdnimg.cn/20200703235519658.png)