前言
为什么要讨论这两个距离之间的区别?
因为,距离函数的选择对数据挖掘算法的效果具有很大的影响,使用错误的距离函数对挖掘过程非常有害。有时候,语义非常相似的对象被认为不相似,而语义不相似的对象却被认为是相似的,这都是因为距离函数选择不佳导致的。这篇文章就是想告诉大家欧式距离不是万能的,距离函数的选择应该随应用场景而定。
欧式距离
设有两个n维数据点 X = ( x 1 , x 2 , . . . , x n ) X=(x_1,x_2,...,x_n) X=(x1,x2,...,xn)和 Y = ( y 1 , y 2 , . . . , y n ) Y=(y_1,y_2,...,y_n) Y=(y1,y2,...,yn)之间的欧几里得距离为:
D i s t ( X , Y ) = ∑ i = 1 n ( x i − y i ) 2 = ( X − Y ) ( X − Y ) T \begin{aligned} Dist(X,Y)=\sqrt{\sum\limits_{i=1}^n(x_i-y_i)^2}=\sqrt{(X-Y)(X-Y)^T} \end{aligned} Dist(X,Y)=i=1∑n(xi−yi)2=(X−Y)(X−Y)T
欧式距离表示的是两点之间的直线距离,它有个很好的性质就是旋转不变性,即两点之间的距离不会因为坐标轴的改变而改变。然而,欧式距离受到数据分布、噪声、高维度和特征度量标准的影响,效果并不太好。
马氏距离
设有 n × m n×m n×m维数据集D,令 S ∈ S\in S∈ R m × m R^{m×m} Rm×m为数据集D的协方差矩阵, X 、 Y X、Y X、Y是数据集D中的任意两行,两个m维行向量的马哈拉诺比斯距离为:
D i s t ( X , Y ) = ( X − Y ) S − 1 ( X − Y ) T \begin{aligned} Dist(X,Y)=\sqrt{(X-Y)S^{-1} (X-Y)^T} \end{aligned} Dist(X,Y)=(X−Y)S−1(X−Y)T
马氏距离不受量纲的影响,即数据测量的单位;也不受数据属性相关性的影响。显然地,若 S − 1 = E S^{-1}=E S−1=E,马氏距离退化为欧式距离。从此可以看出,马氏距离和欧式距离地区别全是因为协方差矩阵S。那么,马氏距离中的 S − 1 S^{-1} S−1到底有什么用?我们看下列证明:
1.根据PCA原理,协方差矩阵进行特征分解能找到消除属性相关性后的基坐标: S = Q Λ Q T S=Q\varLambda Q^T S=QΛQT, Q Q Q的正交列是消除属性相关性的基坐标。
2.坐标旋转后的数据集 F = D Q F=DQ F=DQ,而 D D D的行向量X转换后 F X = X Q T = Q X T F_X=XQ^T=QX^T FX=XQT=QXT
3.F的协方差矩阵:
S F = 1 n F T F − u F T u F = Q T D T D n Q − Q T u D T u D Q = Q T S Q = Λ S_F=\frac{1}{n}F^TF-u_F^Tu_F=Q^T\frac{D^TD}{n}Q-Q^Tu_D^Tu_DQ=Q^TSQ=\varLambda SF=n1FTF−uFTuF=QTnDTDQ−QTuDTuDQ=QTSQ=Λ
故而, Λ \varLambda Λ的对角元素 λ i \lambda_i λi是坐标旋转后F第i个属性的最大化方差。
4.反向推导马氏公式:
d 2 ( X , Y ) = ( X − Y ) S − 1 ( X − Y ) T = ( X − Y ) Q T Q S − 1 Q T Q ( X − Y ) T = ( X − Y ) Q T ( Q T S Q ) − 1 Q ( X − Y ) T = ( F X − F Y ) Λ − 1 ( F X − F Y ) T ( 令 f = F X , h = F Y ) = ( f 1 − h 1 , f 2 − h 2 , . . . , f m − h m ) ( 1 λ 1 1 λ 2 . . . 1 λ m ) ( f 1 − h 1 f 2 − h 2 . . . f m − h m ) = ( f 1 − h 1 λ 1 ) 2 + ( f 2 − h 2 λ 2 ) 2 + . . . + ( f m − h m λ m ) 2 \begin{aligned} d^2(X,Y)=&(X-Y)S^{-1}(X-Y)^T \\=&(X-Y)Q^TQS^{-1}Q^TQ(X-Y)^T \\=&(X-Y)Q^T(Q^TSQ)^{-1}Q(X-Y)^T \\=&(F_X-F_Y)\varLambda^{-1}(F_X-F_Y)^T\text(令f=F_X,h=F_Y) \\=&(f_1-h_1,f_2-h_2,...,f_m-h_m)\begin{pmatrix} \frac{1}{\lambda_1} & & &\\ &\frac{1}{\lambda_2} &&\\&&...&\\&&&\frac{1}{\lambda_m} \end{pmatrix}\begin{pmatrix}f_1-h_1\\f_2-h_2\\...\\f_m-h_m \end{pmatrix} \\=&(\frac{f_1-h_1}{\lambda_1})^2+(\frac{f_2-h_2}{\lambda_2})^2+...+(\frac{f_m-h_m}{\lambda_m})^2 \end{aligned} d2(X,Y)======(X−Y)S−1(X−Y)T(X−Y)QTQS−1QTQ(X−Y)T(X−Y)QT(QTSQ)−1Q(X−Y)T(FX−FY)Λ−1(FX−FY)T(令f=FX,h=FY)(f1−h1,f2−h2,...,fm−hm)⎝⎜⎜⎛λ11λ21...λm1⎠⎟⎟⎞⎝⎜⎜⎛f1−h1f2−h2...fm−hm⎠⎟⎟⎞(λ1f1−h1)2+(λ2f2−h2)2+...+(λmfm−hm)2
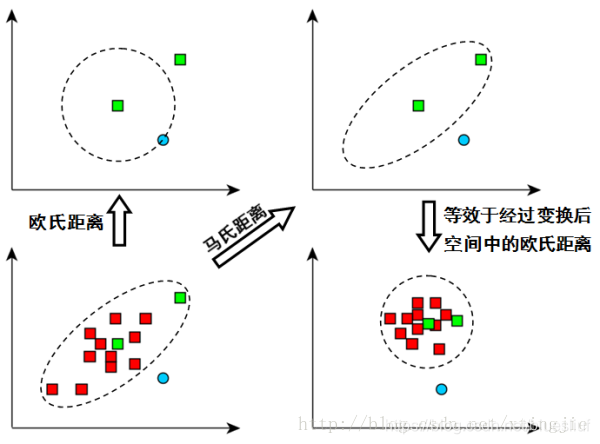
综上所述,马氏距离引入协方差矩阵后实现了两个步骤:坐标旋转和数据压缩。坐标旋转是为了消除属性间相关性的干扰(类似PCA);数据压缩是将坐标差值除以方差,进行了归一化。因为这两个步骤,马氏距离消除了数据分布和特征量纲的影响,这是区别于欧式距离的地方。
两者区别
1.欧式距离受数据分布的影响,马氏距离不会
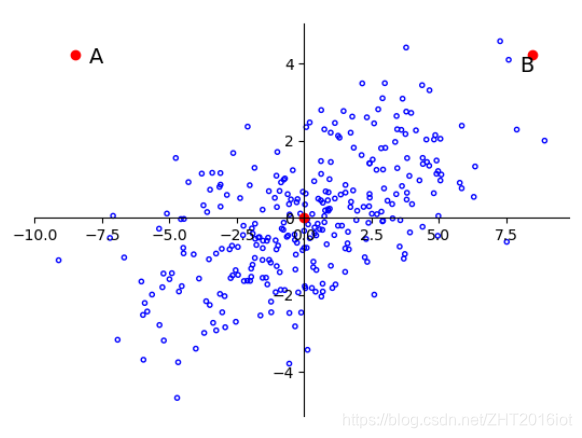
欧式距离只却决于两个点,与其他数据的全局统计性质无关,这毫无疑问是片面的,数据距离应该依赖于全局数据的影响。如下图所示,A的坐标是(-8,4)而B的坐标是(8,4)。毫无疑问,A、B到原点的欧式距离是相同的,那么我们能简单的认为它们与原点O等距吗?答案是不行的。实际上,数据在OB方向上具有较大差异性,是高方差方向。数据在OA方向上很稀疏,是低方差方向。 根据马氏距离除以方差的特性,B到原点的距离是更小的,A到原点的距离是更大的,而这种判断才是合理的。
2.欧氏距离受特征的量纲影响,马氏距离不会
现有两个人张三和李四,他们的身高和体重分别是(170cm,60000g)和(169cm,59000g)。从语义上看张三和李四是很相似的。然而,欧式距离受到g这个单位的影响,两者之间的欧式距离非常大,(60000-59000)2 这个数据非常大使得几乎忽略了身高数据的影响,结果会被误判为非常不相似。而马氏距离除以方差进行了归一化,体重数据间的差异在数值上被缩小,这样才是合理的。
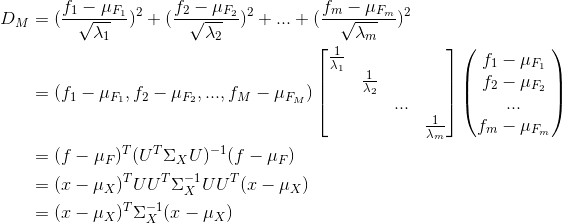





![[机器学习-概念] 什么是欧式距离、标准化欧式距离、马氏距离、余弦距离](https://img-blog.csdnimg.cn/20200703235519658.png)