一、问题的背景
给定一组商品购买信息,找到商品购买中频繁出现的商品集。比如说,我们有如下的商品交易信息:
| Tip | Items |
|---|---|
| 1 | Bread, Milk |
| 2 | Bread, Diaper, Beer, Egg |
| 3 | Milk, Diaper, Beer, Coke |
| 4 | Bread, Milk, Diaper, Beer |
| 5 | Bread, Milk, Diaper, Coke |
我们定义,Itemset 为一系列item的集合,比如:{Milk, Bread, Diaper};定义 k-itemset 为包含k个items的itemset;定义support 是所有交易信息中,包含这个 itemset 的子集。比如s({Milk, Bread, Diaper}) = 2/5;定义frequent Itemset 是一组itemset,它的support 大于等于minsup,这个minsup值由我们自己给定。
为了找出频繁项集,最直观的方法是我们罗列出所有的候选项,然后计算每个候选项的support,最后将满足要求的频繁项保存下来。比如说,我们有M个交易信息储存在数据库中,有N个候选项,那么我们必须要比较MN次,显然它的时间复杂度是非常大的。一个有效的解决途径是我们使用有效的数据结构来存储候选项和交易信息,这样我们不需要将每个候选项与每个交易都匹配一次。
我们可以将候选集储存在哈希树中,这样我们不需要一个交易信息与每一个候选集进行比较,我们只需要比较那些哈希树中存在的候选集。
二、如何构建哈希树
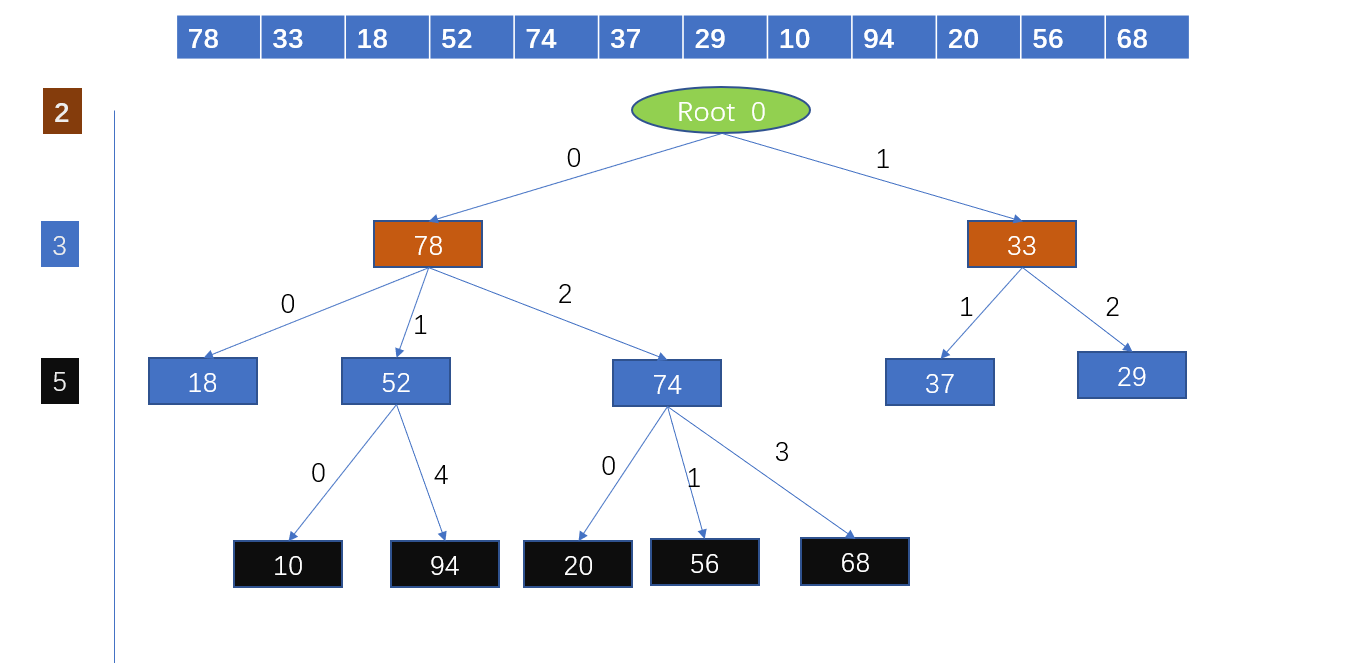
假设我们有15个候选集,长度均为3:
{1 4 5}, {1 2 4}, {4 5 7}, {1 2 5}, {4 5 8}, {1 5 9}, {1 3 6}, {2 3 4}, {5 6 7}, {3 4 5}, {3 5 6}, {3 5 7}, {6 8 9}, {3 6 7}, {3 6 8}
我们需要:1、构建一个hash函数。 2、设定叶子的最大大小(每片叶子中能够存储的最大数据),如果某片叶子中的候选集数量超过了限制,我们需要对这个叶节点做分裂处理。
比如说我们构建了如下图所示的hash函数,在第一个层,对候选集的第一项进行判断,比如说我们对{1,2,5}进行判断,由于第一项为1,因此我们将它放到root的左节点。在第二层,我们对候选集的第二项进行判断,{1,2,5}的第二项是2,根据hash函数,我们再想中间走一步。在第三层,{1,2,5}的第三项是5,因此我们往中间走一步。当然,往下走一步仅在于你当前无法存储在3个节点的情况,因为我们定义了叶子的最大size是3,如果你这个节点能够存储下3个数据,那就没必要继续往下分裂了。
由此我们可以建立如下的哈希树:
那么给定一次商品交易信息,比如[1,2,3,5,6],我们应该如何将这次交易与候选项进行比较?根据hash函数,如果我们想左走,那么我们的选择一定是1开头,然后从[2,3,5,6]选择长度为2的子序列,继续往左走的话,由于[2,3,5,6]与哈希函数中的[1,4,7]无法找到共同项,因此往左走是行不通的,这样我们就避免了这次交易与候选集[1,4,5]的比较。同理我们往中间走,根据哈希函数得到了12[3,5,6]的集合,这样也就是有123,125,126三种可能性,因此与哈希树中对应叶节点的125,458,因此我们知道,在这次交易信息中,125这个候选集出现过一次。因此利用哈希树,我们避免了一部分的比较,减少了比较次数。
三、哈希树的Python实现
class Node:def __init__(self,val=[]):self.val = valself.children = {}class HashTree:def __init__(self):self.root = Node()#建立根节点def insert(self,val):#给定一个值val,创建一个值为val的节点并将其插入到树中root = self.rooti = 0while root.children:#if root has childrenif (val[i]-1) % 3 in root.children.keys():#如果想找的孩子存在root = root.children[(val[i]-1)%3]i += 1else:#if the child doesn't existroot.children[(val[i]-1)%3] = Node([val])return#so the root doesn't have childif len(root.val) < 3:#the value of root is smaller than 3root.val.append(val)returnelse:#root的值的个数已经等于3了,那么我们必须split rootroot.val.append(val)#先把val加入到root的值当中for item in root.val:#对于root值中的的每一项j = (item[i]-1) % 3#表示余数是多少if j in root.children.keys():#如果余数已经在其中了root.children[j].val.append(item)#将item加入到列表中else:root.children[j] = Node()#首先创建该节点root.children[j].val = [item]#如果没有,则创建新列表root.val = [] if len(root.children[j].val) == 4:#分裂节点后,仍然出现了大于3的情况,那么我们需要继续分裂节点i += 1root = root.children[j]for item in root.val:#对于root值中的的每一项j = (item[i]-1) % 3#表示余数是多少if j in root.children.keys():#如果余数已经在其中了 root.children[j].val.append(item)#将item加入到列表中else: root.children[j] = Node()root.children[j].val = [item]#如果没有,则创建新列表root.val = []def PrintTree(self,node):#如何 层次的输出树if not node.val:#如果这个节点的值不存在if not node.children: return#如果孩子也没有else:#有孩子了res = []for item in node.children.values():res += [self.PrintTree(item)]else:#这个节点的值存在return node.valreturn resobj = HashTree()
values = '[{1 2 4}, {1 2 9}, {1 3 5}, {1 3 9}, {1 4 7}, {1 5 8}, {1 6 7}, {1 7 9}, {1 8 9}, {2 3 5}, {2 4 7}, {2 5 6}, {2 5 7}, {2 5 8}, {2 6 7}, {2 6 8}, {2 6 9}, {2 7 8}, {3 4 5}, {3 4 7}, {3 5 7}, {3 5 8}, {3 6 8}, {3 7 9}, {3 8 9}, {4 5 7}, {4 5 8}, {4 6 7}, {4 6 9}, {4 7 8}, {5 6 7}, {5 7 9}, {5 8 9}, {6 7 8}, {6 7 9}]'
values = values.replace('{','[').replace('}',']').replace(' ',',').replace(',,',',')
values = 'values = ' + valuesexec(values)for item in values:obj.insert(item)print(obj.PrintTree(obj.root))