前言

题目： DeepWalk：Online Learning of Social Representations
会议： KDD 2014
论文地址：DeepWalk: Online Learning of Social Representations

总的来说这篇论文算是Network Embedding的开山之作，DeepWalk把神经语言模型Skip-Gram运用在了社区网络中，从而使得深度学习的方法不仅能表示节点还能表示出节点之间的拓扑关系。关于DeepWalk的内容在KDD2016 | node2vec：Scalable Feature Learning for Networks
中有提到过，本文是对DeepWalk更为细致的阐述。

关于node2vec和DeepWalk的详细代码实现过程，会考虑在后面几期内容中给出。

Abstract

本文提出了一种新的学习网络中顶点的潜在表示的方法：DeepWalk。

DeepWalk使用从截断的随机游走中获得的局部信息，通过将游走当作句子的等价形式来学习顶点的潜在表示。

DeepWalk是可扩展的（能够在较短时间内处理大规模网络），它是一种在线学习算法，可以建立有用的增量结果，并且可以简单地并行化。这些特性使得DeepWalk在现实世界中应用广泛，如网络分类和异常检测。

1.Introduction

网络表示的稀疏性既是优点也是缺点：稀疏性使设计高效的离散算法成为可能，但也使其在统计学习中难以推广。网络中的机器学习应用(如网络分类、内容推荐、异常检测和缺失链接预测)必须能够处理这种稀疏性，才能发挥较好的作用。

DeepWalk以一个图作为输入，输出的是每个节点的向量表示。

本文的贡献总结如下：

1. 将深度学习引入到网络图的学习中。
2. 实验结果表明：在网络的标签较为稀疏的情况下，DeepWalk也能取得不错的性能。
3. 通过使用并行实现构建web规模的图表示(如YouTube)来证明了算法的可扩展性。

2.Problem Definition

带节点集和边集的图$G=(V,E)$，$G_L=(V,E,X,Y)$是一个带有部分标签的网络，其中$X$描述了每一个节点的特征，每个特征大小为$S$，$Y$是标签集合。

本文的目标是学习到所有节点的$d$维特征表示$X_E\in R^{|V|\times d}$。

3.Learning Social Representations

学习到的特征表示具有如下性质：

1. 自适应性：网络的演化通常是局部的点和边的变化，这样的变化只会对部分随机游走路径产生影响，因此在网络的演化过程中不需要每一次都重新计算整个网络的随机游走。
2. 社区意识：节点的向量表示间的距离应该可以量化两个节点的相似性。
3. 低维度：当标记数据稀缺时，低维模型具有更好的泛化能力，并且能够加快收敛和推理速度。
4. 连续性：节点的表示向量可以用来模拟连续空间中的部分社区节点。

本文的方法通过使用最初为语言建模而设计的优化技术（Skip-Gram），从短随机游走中学习顶点的表示。 因此接下来会简要回顾随机游走和语言建模的基础知识。

3.1 Random Walks

用$W_{v_i}$表示节点$v_i$的一个长度为$k$的随机游走序列：$(W_{v_i}^1,W_{v_i}^2,...,W_{v_i}^k)$，在内容推荐和社区检测中，这些序列可以被用作各种问题的相似度度量。

使用Random Walks有什么好处？首先，局部探索很容易并行化：多个随机游走程序(在不同的线程、进程或机器中)可以同时探索同一图的不同部分。其次，依靠从短随机游走中获得的信息，可以适应图结构的小变化，而不需要全局重计算。

3.2 Connection: Power laws

那么怎么获得这些随机游走序列呢？一个重要的原则是：如果连通图的度分布遵循幂律分布（无标度网络），则在短随机游走中顶点出现的频率也遵循幂律分布（密度函数是幂函数）。值得注意的是，自然语言中的词频遵循类似的分布。

百度了一下无标度网络： 对于许多现实世界中的复杂网络，如互联网、社会网络等，各节点拥有的连接数（Degree）服从幂律分布。也就是说，大多数“普通”节点拥有很少的连接，而少数“热门”节点拥有极其多的连接。 这样的网络称作无标度网络（Scale-free Network），网络中的“热门”节点称作枢纽节点（Hub）。

图2展示了两种不同的幂律分布：Random Walks中顶点出现的频率分布以及自然语言中的词频分布，从中可以看出二者的相似性。

本文的一个核心贡献就是：Zipf定律可以用于建模网络中的社区结构。 Zipf定律（齐普夫定律）：如果把单词出现的频率按由大到小的顺序排列，则每个单词出现的频率与它的名次的常数次幂存在简单的反比关系。它表明在英语单词中，只有极少数的词被经常使用，而绝大多数词很少被使用。这与无标度网络类似。

3.3 Language Modeling

Language Modeling的目标是：估计一个特定单词序列在语料库中出现的可能性。

给定一个单词序列$W_1^n=(w_0,w_1,...,w_n)$，其中$w_i\in V$，$V$是词库，建模的目标就是在所有训练语料库中使$Pr(w_n|w_0,w_1,...,w_{n-1})$最大化。

将上述概念扩展到网络中（单词对应节点）：在给定之前的随机游走中访问过的所有顶点的情况下，估计观测到顶点$v_i$的可能性，即$Pr(v_i|v_1,v_2,...,v_{i-1})$。

前面已经说过，本文的目标是要学习到每个顶点的特征向量表示，而不仅仅只是节点共现的概率分布。但是节点本身是没法计算的，因此需要引入一个映射函数$\Phi :v\in V\mapsto R^{|V|\times d}$，即将节点映射到其特征表示。因此，我们需要估计以下概率：
$$Pr(v_i|(\Phi (v_1),\Phi (v_2),...,\Phi (v_{i-1})))$$
将顶点转换成向量后就能够进行计算了，具体怎么计算需要用到前面讲的Skip-Gram模型！

在论文阅读：Efficient Estimation of Word Representations in Vector Space
中提出了两种模型：CBOW和Skip-Gram。其中Skip-Gram是使用一个单词来预测上下文（上下文是由出现在给定单词左右的单词组成的）。观察上面概率表达式我们发现右边那部分$(\Phi (v_1),\Phi (v_2),...,\Phi (v_{i-1}))$比较难算，但是如果只是计算一个单词就变得很容易，这与Skip-Gram的思想一致！

同时Skip-Gram消除了对问题的排序约束，即只要在窗口内的单词就都算进来而不用考虑其具体位置，即要求模型最大化任何单词出现在上下文中的概率，而无需知道它与给定单词的偏移量。 类比到网络中将产生以下优化问题：

其中概率部分的意思为：在一个随机游走过程中，给定$v_i$时，出现它的$w$窗口范围内顶点的概率。 简单来说就是在一个游走过程中，出现了$v_i$，那么在该序列中也出现它的$w$窗口范围内这些顶点的概率，这些顶点间没有顺序。

4.Method

本节讨论算法的主要组成部分，由于水平有限，可能解读有误，敬请谅解！

4.1 Overview

在任何语言建模算法中，都只是需要输入语料库和词汇表。而在DeepWalk中，我们将一组随机游走序列作为语料库，图的顶点作为词汇表。

4.2 Algorithm：DeepWalk

DeepWalk由两部分组成：随机游走序列生成器+更新程序。

算法输入：图$G$，窗口长度$w$，嵌入维度$d$，每一个节点$\gamma$个游走序列，每个游走序列长度为$t$。算法输出：每一个节点的向量表示（维度为$d$）。

前面我们讲在计算概率的时候需要引入一个矩阵$\Phi$来将所有节点映射为向量，矩阵$\Phi$中包含$|V|\times d$个参数，这些参数是需要学习的。学习到了矩阵$\Phi$之后，实际上我们也就学习到了所有节点的特征向量表示，也就达到了目的。

类比于神经网络的训练，第1步是对$\Phi$进行初始化。

第2步是搭建一个分类树$T$，实际上就是搭建Hierarchical Softmax，关于Hierarchical Softmax在Skip-Gram一文中也提到过。所谓层次Softmax，就是将词汇表表示为Huffman树，Huffman树将短的二进制代码分配给频繁的单词，这进一步减少了需要评估的输出单元的数量。 输出减少，复杂度就能从$V$下降到$lo{g}_2(V)$。

层次Softmax在后面会进行详细阐述。

第3步开始，循环$\gamma$次，每一次为所有节点生成一个随机游走序列，每生成一个序列就利用Skip-Gram算法来更新参数。

4.2.1 Skip-Gram

具体更新过程如下：

SkipGram算法的输入：当前的$\Phi$，节点$v_i$的一个游走序列$W_{v_i}$以及窗口参数$w$。

对游走序列中的每一个节点$v_j$，取其左右各$w$个节点，对其中每一个节点${\mu }_k$，计算对数概率：
$$-logPr({\mu }_k|\Phi (v_j))$$
概率意为：已知$v_j$的情况下出现${\mu }_k$的概率，每算出一个概率就更新矩阵$\Phi$。

我们可以发现更新的原则就是：对随机游走中的每一个节点，我们都最大化（最小化负的对数概率）以下概率：

举一个具体的例子：

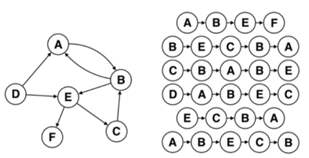
对于顶点$v_4$，它的一个游走序列为$[4,3,1,5,1...]$，对于序列中每一个$v_j$，我们需要利用$\Phi$矩阵来将其映射为一个$d$维向量$\Phi (v_j)$。然后利用$\Phi (v_j)$来计算并最大化条件概率：$Pr({\mu }_k|\Phi (v_j))$，其中${\mu }_k$是$W_{v_4}$中$v_j$前后$w$个节点中的某一个节点。

4.2.2 Hierarchical Softmax

对于给定的${\mu }_k$计算$-logPr({\mu }_k|\Phi (v_j))$的代价比较大，因此将使用分层Softmax来分解条件概率。具体做法：将顶点作为哈夫曼树的叶子，然后最大化特定路径出现的概率：

如果到达顶点${\mu }_k$的路径为$(b_0,b_1,...,b_{\lceil log|V|\rceil })$，则$Pr({\mu }_k|\Phi (v_j))$可以转换为：

而$Pr(b_l|\Phi (v_j))$可以通过分配给节点$b_l$的父节点的二进制分类器来计算：

其中$\Psi (b_l)\in R^d$是节点$b_l$父结点的向量表示。

经过上述复杂地转化后，计算$Pr({\mu }_k|\Phi (v_j))$的复杂度将从$O(|V|)$下降到$O(log|V|)$。

举一个具体的例子：

我们需要计算$Pr(v_3|\Phi (v_1))$：到达顶点$v_3$的路径已知，$\Phi (v_1)$已知，该路径上每一个父节点的向量表示也已知，那么我们就能根据：

和

来计算$Pr(v_3|\Phi (v_1))$。

算出概率后，随后我们更新$\Phi$：$\Phi =\Phi -\alpha \frac{\partial J}{\partial \Phi }$，来最大限度地提高$v_1$和$v_3$同时出现的概率，这样我们算出的每一个节点的特征向量表示将与其游走序列有着很好地对应。

4.2.3 Optimization

总结一下：DeepWalk中需要优化的参数为：$\theta =(\Phi ,\Psi )$，这两个参数在算法的第1步和第2步分别初始化。参数的优化采用SGD，学习率$\alpha$初始时设置为2.5%，学习率会随着到目前为止看到的顶点数的增加而线性减少。

4.3 Parallelizability

前面3.2节有提到：社交网络的随机游走中顶点的频率分布和语言中的单词的频率分布都遵循幂律。 因此参数的更新将是稀疏的。鉴于此，将使用异步SGD(ASGD)来对参数进行更新，尽管本文是在一台机器上使用多线程运行实验，但它已经证明了这种技术是高度可扩展的，并且可以用于非常大规模的机器学习。图4展示了并行DeepWalk的效果：

随着核的增加，并行DeepWalk处理两个网络的速度线性减少，并且相较于连续运行的DeepWalk，并行DeepWalk的预测表现也没有下降。

5.Experimental Design

6.Experiments

第5部分和第6部分的实验细节不再叙述，关于这类算法的实验设计可以参考node2vec中实验的相关细节：KDD2016 | node2vec：Scalable Feature Learning for Networks

7.Related Work

本文方法与前人方法的主要区别可以总结如下：

1. 本文关注的是节点的嵌入表示，而不是计算一些统计数据。
2. 不试图扩展分类过程本身。
3. 提出了一种仅使用本地信息的可扩展的在线方法，大多数其它方法需要全局信息并且是离线的。
4. 将无监督表示学习应用于图。

8.Conclusions

本文提出了一种学习顶点潜在社会表征的新方法：DeepWalk。在极具挑战性的多标签分类任务中，DeepWalk表现出了良好的性能。

作为一种在线算法，DeepWalk是可扩展的：在大规模的图上，DeepWalk的性能明显优于其它几种方法。

DeepWalk还是可并行化的，允许同时更新模型的不同部分。

此外，DeepWalk也是对语言建模的一次总结与概括：语言建模实际上是从不可观察的语言图中采样，语言建模的进步可能会给网络的表示工作带来进步。反之，从可观察图建模中获得的知识反过来也可能会改进对不可观察图的建模。