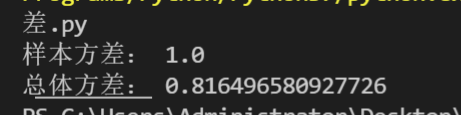
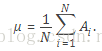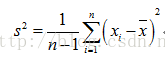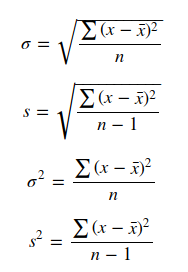总体方差与样本方差分母的小小区别,n还是n-1?
- 引入
- 方差概念
- 方差计算
- 无偏估计
- 样本方差公式
- 相关参考链接
- 样本方差的自由度是n-1
引入
方差概念
方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量,用来度量随机变量和其数学期望(即均值)之间的偏离程度。
方差计算
定义:
D X = E ( X − E X ) 2 = E X 2 − ( E X ) 2 D X=E(X-E X)^{2}=E X^{2}-(E X)^{2} DX=E(X−EX)2=EX2−(EX)2
离散型和连续型的随机变量计算公式分别为:
D ( X ) = { ∑ k = 1 ∞ [ x k − E ( X ) ] 2 p k , ∫ − ∞ ∞ [ x k − E ( X ) ] 2 f ( x ) d x \boldsymbol{D}(\boldsymbol{X})=\left\{\begin{array}{c} {\sum_{k=1}^{\infty}\left[\boldsymbol{x}_{k}-\boldsymbol{E}(\boldsymbol{X})\right]^{2} p_{k},} \\ {\int_{-\infty}^{\infty}\left[\boldsymbol{x}_{k}-\boldsymbol{E}(\boldsymbol{X})\right]^{2} f(\boldsymbol{x}) d \boldsymbol{x}} \end{array}\right. D(X)={∑k=1∞[xk−E(X)]2pk,∫−∞∞[xk−E(X)]2f(x)dx
当给出具体数据进行分析时我们常用到如下两个公式
总体方差:
σ 2 = ∑ i = 1 N ( x i − μ ) 2 N \sigma^{2}=\frac{\sum_{i=1}^{N}\left(x_{i}-\mu\right)^{2}}{N} σ2=N∑i=1N(xi−μ)2
样本方差:
S 2 = 1 n − 1 ∑ i = 1 n ( x i − X ˉ ) 2 S^{2}=\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\bar{X}\right)^{2} S2=n−11i=1∑n(xi−Xˉ)2
那么为什么总体方差和样本方差的分母不同呢?
首先应该明确
1、在用样本方差公式进行计算时,我们并不知道x的分布情况,也不知道 μ \mu μ。 X ˉ \bar{X} Xˉ是所给样本的平均值,其值并不一定等于 μ \mu μ。
2、总体方差是确定的,是综合所有数据后得到的方差,同理, μ \mu μ也是由所有数据得到的确数。而 X ˉ \bar{X} Xˉ和 S 2 S^{2} S2是根据部分数据对 μ \mu μ和 σ 2 \sigma^{2} σ2进行估计。
3、总体方差:
也叫做有偏估计,其实就是我们从初高中就学到的那个标准定义的方差,除数是N。如果实现已知期望值,比如测水的沸点,那么测量10次,测量值和期望值之间是独立的(期望值不依测量值而改变,随你怎么折腾,温度计坏了也好,看反了也好,总之,期望值应该是100度),那么E『(X-期望)^2』,就有10个自由度。事实上,它等于(X-期望)的方差,减去(X-期望)的平方。” 所以叫做有偏估计,测量结果偏于那个”已知的期望值“。
样本方差:
无偏估计、无偏方差(unbiased variance)。对于一组随机变量,从中随机抽取N个样本,这组样本的方差就是Xi^2平方和除以N-1。这可以推导出来的。如果现在往水里撒把盐,水的沸点未知了,那我该怎么办? 我只能以样本的平均值,来代替原先那个期望100度。 同样的过程,但原先的(X-期望),被(X-均值)所代替。 设想一下(Xi-均值)的方差,它不在等于Xi的方差, 而是有一个协方差,因为均值中,有一项Xi/n是和Xi相关的,这就是那个"偏"的由来
样本方差与总体方差的区别
我们先讨论一个样本时:
(此段引自 link.)
对于样本方差来说,假如从总体中只取一个样本,即n=1,那么样本方差公式的分子分母都为0——方差完全不确定。这很好理解,因为样本方差是用来估 计总体中个体之间的变化大小,只拿到一个个体,当然完全看不出变化大小。反之,如果公式的分母不是n-1而是n,计算出的方差就是0——这是不合理的,因 为不能只看到一个个体就断定总体的个体之间变化大小为0。
对于总体方差来说,假如总体中只有一个个体,即N=1,那么方差,即个体的变化,当然是0。如果分母是N-1,总体方差为0/0,即不确定,却是不合理的——总体方差不存在不确定的情况。
以上可帮助理解两式的正确性,关于样本方差的理论推导如下:
首先回顾一下无偏估计
无偏估计
无偏估计是用样本统计量来估计总体参数时的一种无偏推断。估计量的数学期望等于被估计参数的真实值,则称此此估计量为被估计参数的无偏估计,即具有无偏性,是一种用于评价估计量优良性的准则。无偏估计的意义是:在多次重复下,它们的平均数接近所估计的参数真值。
估计总体平均值μ时,若以样本平均值ξ’为估计量,则可算得ξ’的数学期望E(ξ’)=μ,这说明ξ’是总体平均值μ的无偏估计。
介绍无偏估计的意义就是,我们计算的样本方差,希望它是总体方差的一个无偏估计
样本方差公式
假如样本方差公式为如下形式
S 2 = 1 n ∑ i = 1 n ( x i − X ˉ ) 2 S^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{X}\right)^{2} S2=n1i=1∑n(xi−Xˉ)2
此时我们可以判断一下它是否为总体方差的一个无偏估计,即判断 E ( S 2 ) E\left(S^{2}\right) E(S2)是否为 σ 2 \sigma^{2} σ2。
E [ S 2 ] = E [ 1 n ∑ i = 1 n ( X i − X ˉ ) 2 ] = E [ 1 n ∑ i = 1 n ( ( X i − μ ) − ( X ˉ − μ ) ) 2 ] = E [ 1 n ∑ i = 1 n ( ( X i − μ ) 2 − 2 ( X ˉ − μ ) ( X i − μ ) + ( X ˉ − μ ) 2 ) ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − 2 n ( X ˉ − μ ) ∑ i = 1 n ( X i − μ ) + 1 n ( X ˉ − μ ) 2 ∑ i = 1 n 1 ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − 2 n ( X ˉ − μ ) ∑ i = 1 n ( X i − μ ) + ( X ˉ − μ ) 2 ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − 2 n ( X ˉ − μ ) ∑ i = 1 n ( X i − μ ) + ( X ˉ − μ ) 2 ] \begin{aligned} \mathrm{E}\left[S^{2}\right] &=\mathrm{E}\left[\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}\right]=\mathrm{E}\left[\frac{1}{n} \sum_{i=1}^{n}\left(\left(X_{i}-\mu\right)-(\bar{X}-\mu)\right)^{2}\right] \\ &=\mathrm{E}\left[\frac{1}{n} \sum_{i=1}^{n}\left(\left(X_{i}-\mu\right)^{2}-2(\bar{X}-\mu)\left(X_{i}-\mu\right)+(\bar{X}-\mu)^{2}\right)\right] \\ &=\mathrm{E}\left[\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2}-\frac{2}{n}(\bar{X}-\mu) \sum_{i=1}^{n}\left(X_{i}-\mu\right)+\frac{1}{n}(\bar{X}-\mu)^{2} \sum_{i=1}^{n} 1\right] \\ &=\mathrm{E}\left[\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2}-\frac{2}{n}(\bar{X}-\mu) \sum_{i=1}^{n}\left(X_{i}-\mu\right)+(\bar{X}-\mu)^{2}\right] \\ &=\mathrm{E}\left[\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2}-\frac{2}{n}(\bar{X}-\mu) \sum_{i=1}^{n}\left(X_{i}-\mu\right)+(\bar{X}-\mu)^{2}\right] \end{aligned} E[S2]=E[n1i=1∑n(Xi−Xˉ)2]=E[n1i=1∑n((Xi−μ)−(Xˉ−μ))2]=E[n1i=1∑n((Xi−μ)2−2(Xˉ−μ)(Xi−μ)+(Xˉ−μ)2)]=E[n1i=1∑n(Xi−μ)2−n2(Xˉ−μ)i=1∑n(Xi−μ)+n1(Xˉ−μ)2i=1∑n1]=E[n1i=1∑n(Xi−μ)2−n2(Xˉ−μ)i=1∑n(Xi−μ)+(Xˉ−μ)2]=E[n1i=1∑n(Xi−μ)2−n2(Xˉ−μ)i=1∑n(Xi−μ)+(Xˉ−μ)2]
其中 ∑ i = 1 n ( X i − μ ) \sum_{i=1}^{n}\left(X_{i}-\mu\right) ∑i=1n(Xi−μ)= ∑ i = 1 n X i \sum_{i=1}^{n} X_{i} ∑i=1nXi– ∑ i = 1 n μ \sum_{i=1}^{n} \mu ∑i=1nμ= ∑ i = 1 n X i \sum_{i=1}^{n} X_{i} ∑i=1nXi–n μ \mu μ=n X ˉ \bar{X} Xˉ–n μ \mu μ
故 E [ S 2 ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − 2 n ( X ˉ − μ ) ∑ i = 1 n ( X i − μ ) + ( X ˉ − μ ) 2 ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − 2 n ( X ˉ − μ ) ⋅ n ⋅ ( X ˉ − μ ) + ( X ˉ − μ ) 2 ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − 2 ( X ˉ − μ ) 2 + ( X ˉ − μ ) 2 ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 ] − E [ ( X ˉ − μ ) 2 ] = σ 2 − E [ ( X ˉ − μ ) 2 ] \begin{aligned} \mathrm{E}\left[S^{2}\right] &=\mathrm{E}\left[\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2}-\frac{2}{n}(\bar{X}-\mu) \sum_{i=1}^{n}\left(X_{i}-\mu\right)+(\bar{X}-\mu)^{2}\right] \\ &=\mathrm{E}\left[\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2}-\frac{2}{n}(\bar{X}-\mu) \cdot n \cdot(\bar{X}-\mu)+(\bar{X}-\mu)^{2}\right] \\ &=\mathrm{E}\left[\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2}-2(\bar{X}-\mu)^{2}+(\bar{X}-\mu)^{2}\right] \\ &=\mathrm{E}\left[\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2}\right]-\mathrm{E}\left[(\bar{X}-\mu)^{2}\right] \\ &=\sigma^{2}-\mathrm{E}\left[(\bar{X}-\mu)^{2}\right] \end{aligned} E[S2]=E[n1i=1∑n(Xi−μ)2−n2(Xˉ−μ)i=1∑n(Xi−μ)+(Xˉ−μ)2]=E[n1i=1∑n(Xi−μ)2−n2(Xˉ−μ)⋅n⋅(Xˉ−μ)+(Xˉ−μ)2]=E[n1i=1∑n(Xi−μ)2−2(Xˉ−μ)2+(Xˉ−μ)2]=E[n1i=1∑n(Xi−μ)2]−E[(Xˉ−μ)2]=σ2−E[(Xˉ−μ)2]
其中
E [ ( X ˉ − μ ) 2 ] = 1 n σ 2 \mathrm{E}\left[(\bar{X}-\mu)^{2}\right]=\frac{1}{n} \sigma^{2} E[(Xˉ−μ)2]=n1σ2
故:
E [ 1 n ∑ i = 1 n ( X i − X ˉ ) 2 ] = σ 2 − 1 n σ 2 = n − 1 n σ 2 E\left[\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}\right]=\sigma^{2}-\frac{1}{n} \sigma^{2}=\frac{n-1}{n} \sigma^{2} E[n1i=1∑n(Xi−Xˉ)2]=σ2−n1σ2=nn−1σ2
但我们要得到总体方差的一个无偏估计
n n − 1 E [ 1 n ∑ i = 1 n ( X i − X ˉ ) 2 ] = E [ 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) 2 ] = σ 2 \frac{n}{n-1} E\left[\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}\right]=E\left[\frac{1}{n-1} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}\right]=\sigma^{2} n−1nE[n1i=1∑n(Xi−Xˉ)2]=E[n−11i=1∑n(Xi−Xˉ)2]=σ2
所以样本方差的分母为n–1而不是n。
相关参考链接
link1为什么样本方差(sample variance)的分母是 n-1?.
其中还包含用 S 2 = 1 n ∑ i = 1 n ( X i − μ ) 2 S^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\mu\right)^{2} S2=n1∑i=1n(Xi−μ)2来近似 σ 2 \sigma^{2} σ2等详细步骤。

link2彻底理解样本方差为何除以n-1.
样本方差的自由度是n-1
参看自由度(为什么样本方差自由度是n-1)
其中讨论了离差平方和 S S = ∑ ( x i − x ˉ ) 2 S S=\sum\left(x_{i}-\bar{x}\right)^{2} SS=∑(xi−xˉ)2,
总体方差 D ( x ) = S S n D(x)=\frac{S S}{n} D(x)=nSS,样本方差 D ( x ) = S S n − 1 D(x)=\frac{S S}{n-1} D(x)=n−1SS
生动举例解释为什么样本方差自由度为n-1