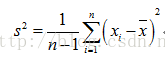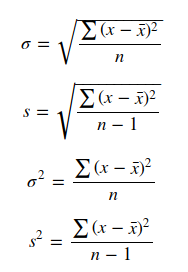1.有偏样本方差、无偏样本方差

笔记来源：Why Dividing By N Underestimates the Variance

1.1 为什么样本方差总是小于总体方差？

由于总体量太大，我们要耗费大量人力物力财力才可以或者永远无法了解总体情况，所以我们只能用样本数据来估计总体的情况，为方便进行解释下面我们假设了一个总体均值

样本均值 $\bar{x}=17.6$，有偏样本方差 ${\sigma }_{X_1}^2=81.4$
假设的总体均值 $\mu =20$，总体方差 ${\sigma }^2=87.2$
$${\sigma }_{X_1}^2<{\sigma }^2$$

例2：另一组样本数据
样本均值 $\bar{x}=22.6$，有偏样本方差 ${\sigma }_{X_2}^2=105$
假设的总体均值 $\mu =20$，总体方差 ${\sigma }^2=112$
$${\sigma }_{X_2}^2<{\sigma }^2$$

1.2 为什么方差不能用绝对值？

我们通过对方差的公式求导来找到最小方差

当我们将方差公式中的平方替换为绝对值时，我们无法找到最小方差，因为在最小处不可导