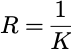如何画一个简单的波特图(渐近线近似&零极点特性)?
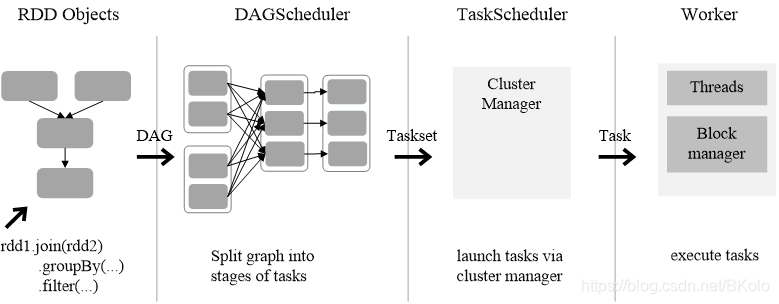
在工程上我们常见下图所示的波特图来描述一个系统开环函数的频率特性,通过零点和极点画出波特图我们可以得到系统是否稳定的结论。

首先讲一下人们为什么要使用波特图:
由于在研究一个模拟系统的频率相应时,信号的频率范围很宽,通常从Hz级到GHz级,如果用线性线性坐标画系统函数的幅频特性和相频特性曲线,动态范围和精度之间的矛盾不可避免,因此使用对数坐标,将会压缩坐标,扩大观察的视野,解决了前述矛盾。

如上图所示,横坐标频率每增大一个单位,即表示频率增大10倍,就是我们常说的“10倍频程”。 应当注意的是,如果波特图具有负半轴,并不表示小于0的频率,而是表示为 ω \omega ω小于1的频率。 如果需要小于0的频率特性,利用系统频率特性的共轭对称特性可以得到。
对于纵坐标而言,幅频特性曲线表示为dB,而相频特性依旧用°(degree)表示。
波特图又分为开环波特图( G ( s ) G(s) G(s))和闭环波特图( H ( s ) H(s) H(s)),两者能够提供的信息也不一样。
- 开环波特图能够提供的信息:
- 开环频率响应,进而可以通过图解法(如向量图/等M圆图/等N圆图)求得闭环频率响应
- 通过观察相位裕度/幅值裕度来判断系统的稳定性,一般来说在幅值穿越频率点处的相位阈值为50°-60°比较合适,最低不能小于45°。
- 开环伯德图的形状也可以用来表征闭环系统的响应特性,如下图所示:

- 闭环波特图可以提供系统全部频率响应特性,也能与时域响应联系起来。通过闭环波特图我们能够对系统的性能进行评估,根据实际情况选择合适的系统。
本文主要讨论的是开环函数的波特图,由于其幅频特性通常以对数坐标轴上的一条直线为渐近线,因此幅频特性的曲线通常可以只画渐近线来表示系统的一些特征。
一般系统的开环函数可以表示为:
G ( j ω ) = G 0 ∏ i = 1 m ( j ω − z i ) ∏ j = 1 n ( j ω − p j ) G(j\omega) = G_{0} \frac{ \prod_{i=1}^{m} ({j\omega - z_{i}}) }{ \prod_{j=1}^{n} ({j\omega - p_{j}}) } G(jω)=G0∏j=1n(jω−pj)∏i=1m(jω−zi)
G ( j ω ) = 20 l o g ∣ G ( j ω ) ∣ G(j\omega)=20log|G(j\omega)| G(jω)=20log∣G(jω)∣ 归一化处理,可化简为:
= 20 l o g ∣ G 0 ∗ ∣ + ∑ i = 1 m 20 ( l o g ∣ j ω z i − 1 ∣ + l o g z i ) − ∑ j = 1 n 20 ( l o g ∣ j ω p j − 1 ∣ + l o g p i ) =20log|G_0^*|+ \sum_{i=1}^{m}{20(log| \frac{j\omega}{z_i}-1|} +log{z_i})- \sum_{j=1}^{n}{20(log| \frac{j\omega}{p_j}-1|} +log{p_i}) =20log∣G0∗∣+∑i=1m20(log∣zijω−1∣+logzi)−∑j=1n20(log∣pjjω−1∣+logpi)
= 20 l o g ∣ G 0 ∗ ∣ + ∑ i = 1 m 20 l o g 1 + ( ω z i ) 2 − ∑ j = 1 n 20 l o g 1 + ( ω p j ) 2 + C o n s t a n t =20log|G_0^*|+ \sum_{i=1}^{m}{20log\sqrt{1+(\frac{\omega}{z_i})^2}} - \sum_{j=1}^{n}{20log \sqrt{ 1 + (\frac{\omega}{p_j})^2}}+Constant =20log∣G0∗∣+∑i=1m20log1+(ziω)2−∑j=1n20log1+(pjω)2+Constant
ϕ ( ω ) = 0 ° o r − 180 ° + ∑ i = 1 m a r c t a n ( ω − z i ) − ∑ j = 1 n a r c t a n ( ω − p j ) \phi(\omega)=0° or -180° + \sum_{i=1}^{m}{arctan(\frac{\omega}{-z_i})} - \sum_{j=1}^{n}{arctan(\frac{\omega}{-p_j})} ϕ(ω)=0°or−180°+∑i=1marctan(−ziω)−∑j=1narctan(−pjω)
由上面的公式可知,在对数域,系统开环函数的零极点幅频特性、相频特性都满足线性叠加关系。 l o g ω = 0 log \omega=0 logω=0时的初始值由 ω = 1 \omega=1 ω=1状态下的幅度和相位决定。
-
首先考虑常数项 G 0 ∗ G_0^* G0∗,幅频特性为 20 l o g ∣ G 0 ∣ 20log|G_0| 20log∣G0∣;当 G 0 ∗ > 0 G_0^*>0 G0∗>0时,对相频特性的影响表现为0°,当 G 0 ∗ < 0 G_0^*<0 G0∗<0时,对相频特性的影响表现为-180°。
-
接下来考虑零点叠加项的影响,幅频特性为 ∑ i = 1 m 20 l o g 1 + ( ω z i ) 2 \sum_{i=1}^{m}{20log\sqrt{1+(\frac{\omega}{z_i})^2}} ∑i=1m20log1+(ziω)2,当 ω ≪ z i \omega \ll z_i ω≪zi的时候, 1 + ( ω z i ) 2 ≈ 1 = 0 d B \sqrt{1+(\frac{\omega}{z_i})^2}≈1=0 dB 1+(ziω)2≈1=0dB,当 ω ≫ z i \omega \gg z_i ω≫zi的时候, 1 + ( ω z i ) 2 ≈ z i ω = 20 l o g ω z i d B \sqrt{1+(\frac{\omega}{z_i})^2}≈\frac{z_i}{\omega}=20log\frac{\omega} {z_i}dB 1+(ziω)2≈ωzi=20logziωdB,每10倍频程多增加20 dB。因此可以用在 w i w_i wi处的拐点的渐近线表示,即斜率此时从0dB变为+ 20 dB/10倍频(即每倍频程增加6 dB)。因为零点的叠加特性,当 w ≫ z n w \gg z_n w≫zn时,斜率增加+ (n*20)dB / 10倍频。与横坐标的交点表示 ∣ G ( j w ) ∣ = 1 = 0 d B |G(jw)|=1=0dB ∣G(jw)∣=1=0dB。
-
对于相频特性来说,当 ω ≪ z i \omega \ll z_i ω≪zi的时候,带来的相位改变为180°,在当 ω = z i \omega = z_i ω=zi的时候,带来的相位改变为135°(假设 w i > 0 w_i>0 wi>0,那么 j ω − z i {j\omega - z_{i}} jω−zi在复平面上为第二象限,因此幅角为钝角),当 w ≫ z i w \gg z_i w≫zi时,带来的相位改变是90°。( z i < 0 z_i<0 zi<0时符号发生变化)
-
极点与零点的符号相反,因此,每增加一个极点,幅频特性的斜率就要多- 20 dB / 10倍频,比如从- 20 dB / dec变到- 40 dB / dec。相频特性的符号也与零点相反,当 w ≫ p i w \gg p_i w≫pi时,带来的相位改变由0°到-45°,再到-90°。
(说人话!) 好的,下面就来进行一个通俗易懂的规律总结,零极点对于波特图的影响如下:
a. 每一个极点会给幅频响应带来一个-20dB/10倍频程斜率的变化,每一个零点会给幅频响应带来一个+20dB/10倍频程斜率的变化。
b.每一个极点会给相频响应带来一个-90°的相位变化,每一个零点会给相频响应带来一个+90°的相位变化。
另外,最近在B站上刷视频的时候发现一个很有意思的想法(与从系统函数的零极点出发不同,利用的是系统函数的级联特性):由于波特图的可加性,一个复杂系统的幅频响应可以差分为若干个简单子系统的级联,那么把简单子系统的波特图分别画出来、相加之后就是复杂系统的波特图。
视频链接为 https://www.bilibili.com/video/BV1yt411c7W8 讲得很不错,推荐~
比如我们可以熟悉一些常见的简单系统的波特图: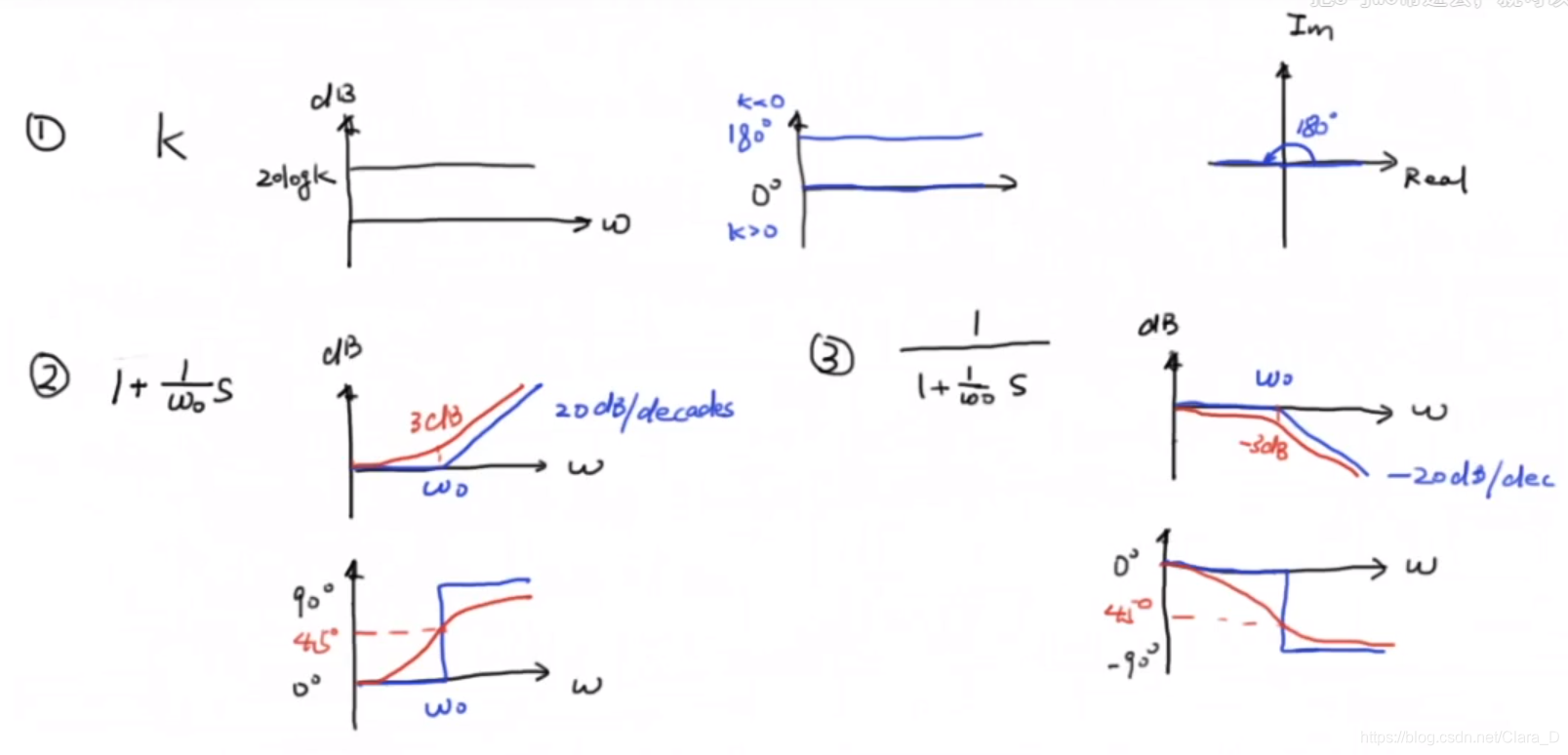
下面举一个复杂系统利用这些常见的简单波特图拆分、然后相加得到自身波特图的例子:
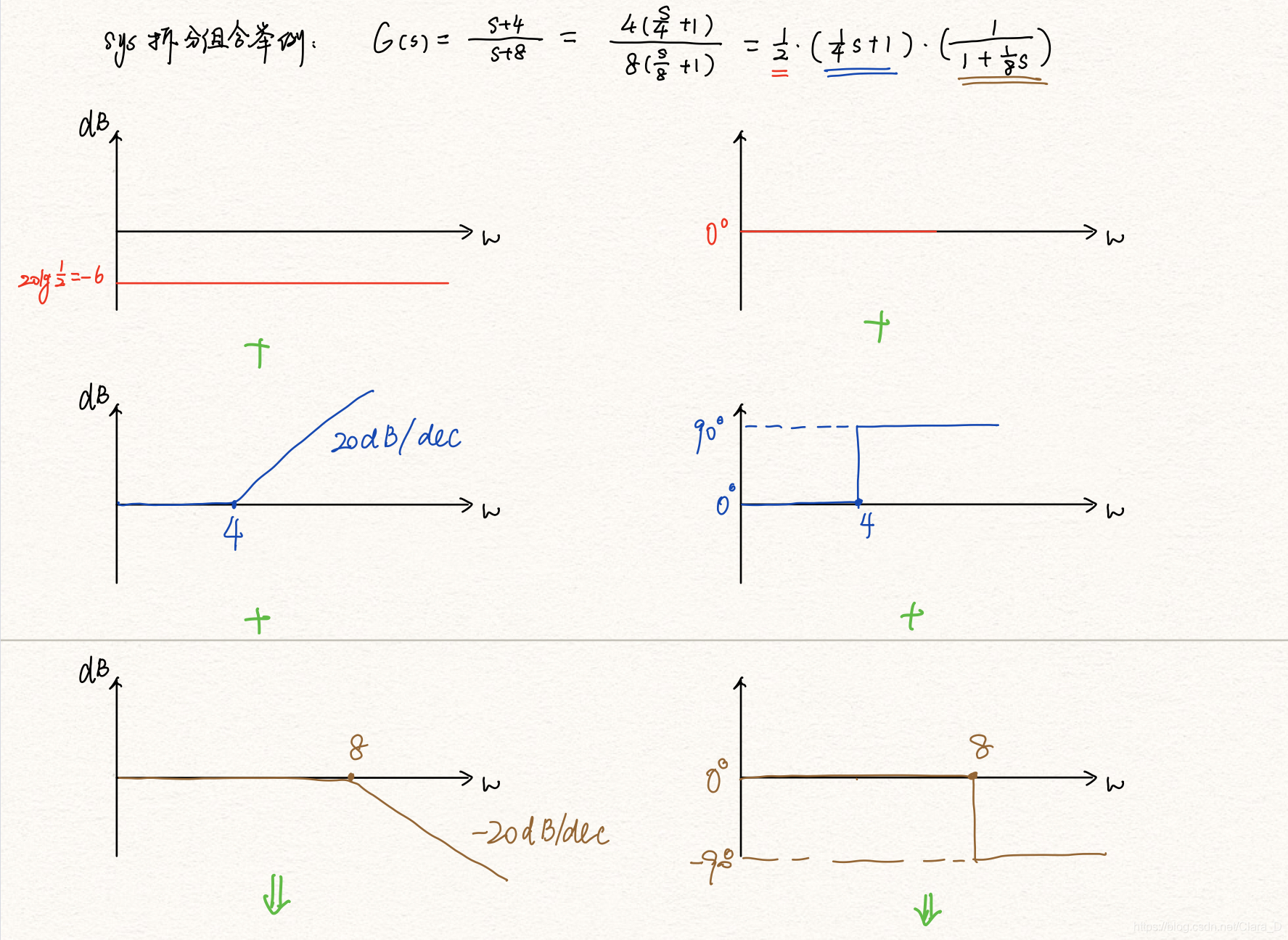
将所有子系统的波特图相加可以得到:
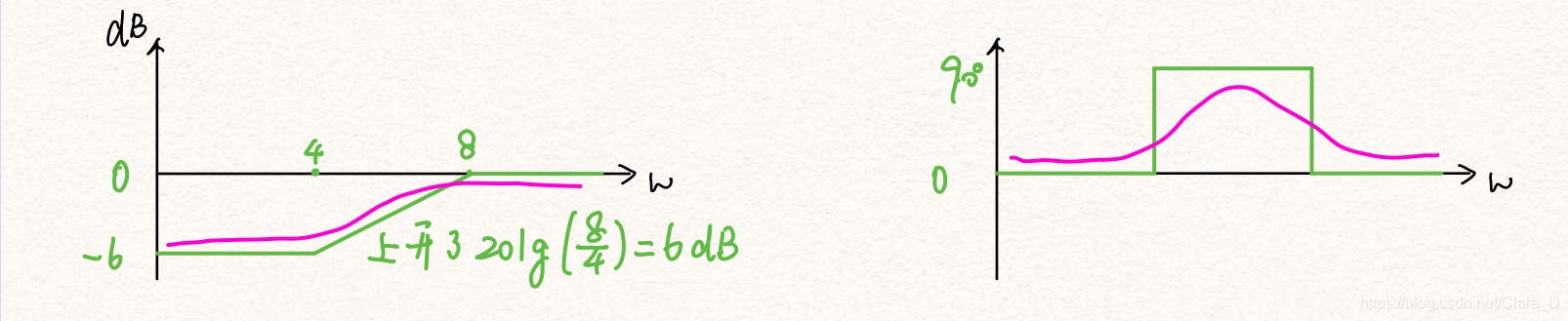
而实际中的系统框图也可以表示为:

因此,当我们已知一个系统的波特图特征,要求系统函数时,可以根据波特图的情况拆分为多个子系统的波特图叠加,然后分别求出子系统的系统函数,最后级联相乘就可以得到最终的系统函数了。这对于我们实际的系统设计中也是有启发的。
另外,提一个问题,你知道为什么波特图的横坐标要用频率表示吗?思考之后把你的答案写在评论区吧~