打家劫舍系列总共有三道，难度设计非常合理，层层递进。第一道是比较标准的动态规划问题，而第二道融入了环形数组的条件，第三道更绝，让盗贼在二叉树上打劫.
House Robber |

public int rob(int[] nums);

题目很容易理解，而且动态规划的特征很明显。解决动态规划问题就是找「状态」和「选择」。
假想你就是这个专业强盗，从左到右走过这一排房子，在每间房子前都有两种选择：抢或者不抢。
如果你抢了这间房子，那么你肯定不能抢相邻的下一间房子了，只能从下下间房子开始做选择。
如果你不抢这间房子，那么你可以走到下一间房子前，继续做选择。
当你走过了最后一间房子后，你就没得抢了，能抢到的钱显然是 0（base case）。
以上的逻辑很简单吧，其实已经明确了「状态」和「选择」：你面前房子的索引就是状态，抢和不抢就是选择。
状态表示：dp[i][0/1]表示第i个房子偷或不偷的最高金额
初始边界：dp[0][] = {0,0}
转移方程：
当前房子不偷：dp[i][1] = dp[i-1][0] + nums[i]
当前房子偷： dp[i][0] = max{dp[i-1][0],dp[i-1][1]}

int rob(vector<int>& nums) {vector<vector<int>> dp(nums.size()+1,vector<int>(2,0));for(int i = 1; i <= nums.size(); i++){dp[i][0] = max(dp[i-1][1],dp[i-1][0]);dp[i][1] = dp[i-1][0] + nums[i-1];}return max(dp[nums.size()][0],dp[nums.size()][1]);
}

间复杂度：O（N）
空间复杂度：O（N）
优化：用四个变量表示代替上面的状态

int rob(vector<int>& nums) {int n = nums.size();int last_0 = 0, last_1 = 0, curr_0 = 0, curr_1 = 0;for(int i = 0; i < nums.size(); i++){curr_0 = max(last_0, last_1);curr_1 = last_0 + nums[i];last_0 = curr_0;last_1 = curr_1;}return max(curr_0, curr_1);
}

时间复杂度：O（N）
空间复杂度：O（1）

打家劫舍II（动态规划）

这道题目和第一道描述基本一样，强盗依然不能抢劫相邻的房子，输入依然是一个数组，但是告诉你这些房子不是一排，而是围成了一个圈。

也就是说，现在第一间房子和最后一间房子也相当于是相邻的，不能同时抢。比如说输入数组 nums=[2,3,2]，算法返回的结果应该是 3 而不是 4，因为开头和结尾不能同时被抢。
那么就会有这两种情况：
第一间房子抢的化最后一间房子就不能抢
最后一间房子抢的话第一间房子就不能抢
所以结合打家劫舍I我们可以实现这样种情况，然后返回这两种情况的最大值就是答案。

    int rob(vector<int>& nums) {if(nums.size() == 0) return 0;if(nums.size() == 1) return nums[0];// 第一间房子抢的化最后一间房子就不能抢vector<int> nums1(nums.begin()+1,nums.end());// 最后一间房子抢的话第一间房子就不能抢vector<int> nums2(nums.begin(),nums.end()-1);// 取两者最大值return max(rob2(nums1),rob2(nums2));}int rob2(vector<int>& nums) {int pre = 0,curr = 0;for(int i = 0; i < nums.size(); i++){int tmp = curr;curr = max(curr,pre + nums[i]);pre = tmp;}return curr;}

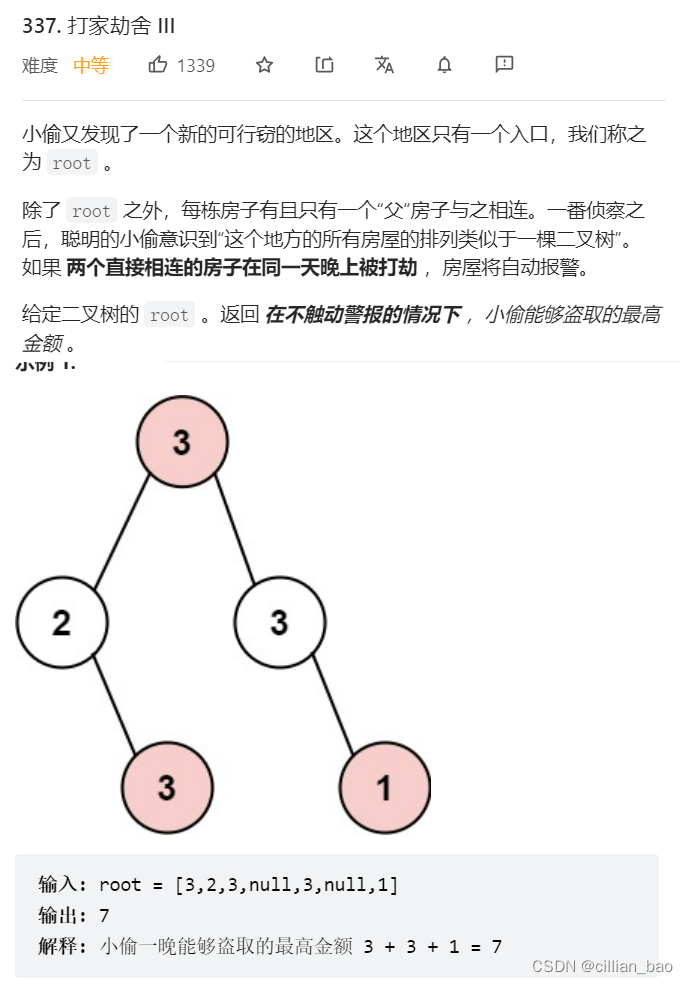
打家劫舍III（树型DP）

状态转移方程：
当前房子偷 = 左房子不偷 + 右房子不偷 + 当前房子的钱
当前房子不偷 = max(左房子不偷，左房子偷) + max(右房子不偷，右房子偷)

函数maxPrifox：返回的是偷和不偷的最优策略对应的结果值

    struct data{int y; // 偷int n; // 不偷};int rob(TreeNode* root) {if(!root) return 0;data rs =  maxPrifox(root);return max(rs.y, rs.n);}data maxPrifox(TreeNode* root){if(!root) return {0, 0};// 1. 拿到左房子的所有状态信息data le = maxPrifox(root->left);// 2. 拿到右房子的所有状态信息data ri = maxPrifox(root->right);data rs;// 3. 当前房子偷 = 左房子不偷 + 右房子不偷 + 当前房子的钱rs.y = le.n + ri.n + root->val;// 4. 当前房子不偷 = max(左房子不偷，左房子偷) + max(右房子不偷，右房子偷)rs.n = max(ri.y, ri.n) + max(le.y, le.n);return rs;}