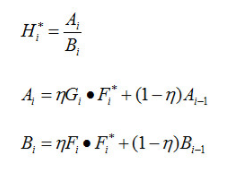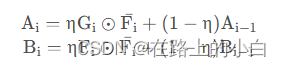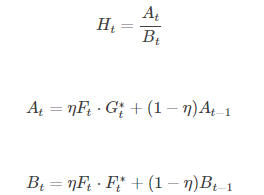文章标题：《Visual Object Tracking using Adaptive Correlation Filters》
文章地址：http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.294.4992&rep=rep1&type=pdf
文章代码：（python）https://github.com/opencv/opencv/blob/master/samples/python/mosse.py
（C++）https://github.com/opencv/opencv_contrib/blob/master/modules/tracking/samples/tutorial_customizing_cn_tracker.cpp

2010年CVPR的一篇的文章

Abstract

相关滤波器（correlation filters）虽然用得不多，但是在物体被旋转、遮挡或者有其它干扰的复杂情况下实施跟踪，速度要比当前的先进技术快 $20$ 倍。最古老、最简单的相关滤波器使用了简单的模板，实际跟踪时不太好用。ASEF 和 UMACE 等现代一点的方法性能好一点，但是它们的训练需求不太适应用于跟踪。视觉跟踪任务要求从单帧图像训练出鲁棒的滤波器，并且在跟踪过程中，根据目标外观的变化进行动态调整。

本文提出了一种新型相关滤波器：MOSSE（Minimum Output Sum of Squared Error），我们在初始化的时候，从一帧图像中产生稳定的相关滤波器。基于MOSSE滤波器的跟踪器以每秒 $669$ 帧的速度运行，对光照、比例、姿态和非刚性变形的变化具有鲁棒性。跟踪的时候根据峰值与旁瓣比（peak-to-sidelobe ratio，PSR）判断是否发生遮挡，以此决定是否暂停跟踪，等物体重新出现时恢复跟踪。

具体做法

获取选区：

首先把输入图像转为灰度图，选取跟踪区域。修改选区框的尺寸，使得该尺寸是做离散傅里叶变换的最佳尺寸。
然后根据选区创建汉宁窗（HanningWindow），它用于突出图像中心区域，减弱图像边缘区域。（这个后面用到）
把它裁剪出来，得到输入数据 $f$ ：

在这里插入图片描述

预处理：

常规操作。把输入图像 $f$ 的数据取对数，使数据无偏，符合正态分布。对数效果示意图：
在这里插入图片描述
然后减均值，除以方差，把数据标准化（Normaization）。

最后乘以汉宁窗。

建立求解目标：

设置我们对该选区的期望输出响应 $g$ 。它是一个中间值很大，四周值很小的矩形图片，尺寸和选区尺寸一样大。
可视化如下：

在这里插入图片描述

(图1)

（具体做法可以看代码）

我们希望训练得到一个相关过滤器 $\color{red}h$ ，使 $f ☆ h = g$ ：

在这里插入图片描述

其中符号 $☆$ 表示做 “相关” 运算。

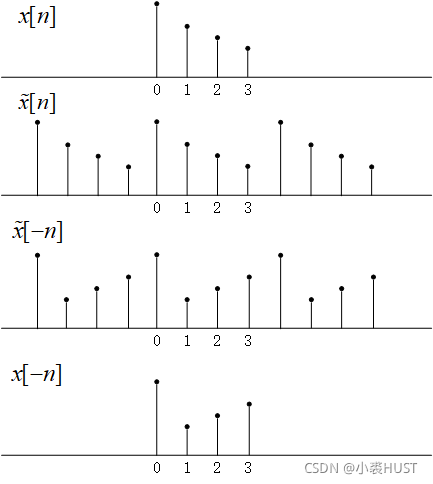
“相关” 运算和 “卷积” 运算很像，二维情况下，对卷积核关于 $2$ 个轴先后旋转 $180^{\circ}$ ，再做卷积，就是 “相关”。
所以主要是 “核” 不同。具体去网上查资料或者看冈萨雷斯的《数字图像处理》(第四版) p101。

如果训练良好，这个相关过滤器 $h$ 大概长这样：

在这里插入图片描述

怎样找到 $h$ 呢？

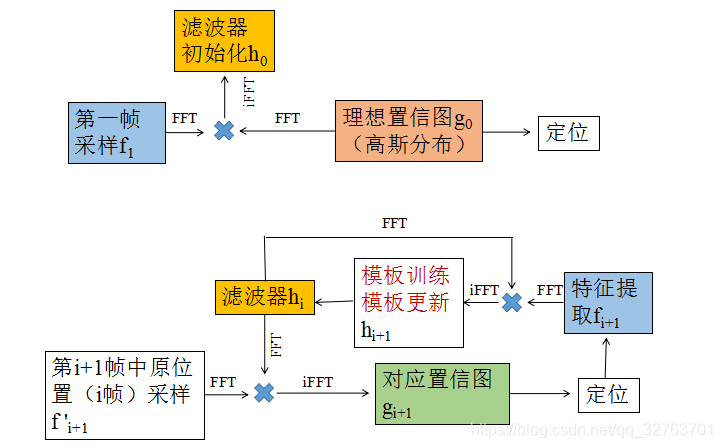
我们知道在傅里叶域做乘法相当于在空间域做卷积，于是先通过快速傅里叶变换 ( $F F T$ ) 把数据从图像空间域转到傅里叶域，然后在傅里叶域进行操作，这样可以减少计算量。我们用对应的大写字母表示傅里叶域的数据：

输入图像： $\mathcal{F}(f)$ ，相关过滤器： $\mathcal{F}(h)$ ，输出响应： $\mathcal{F}(g)$ 。

于是相关运算在傅里叶域表示为： $\; \odot \; H^* = G \tag{1}$

其中符号 $\odot$ 表示逐个元素的相乘，符号 $*$ 表示复共轭，也就是虚部取相反的符号。

这个运算的速度主要取决于傅里叶变换和傅里叶逆变换，时间复杂度上限是 $O (P l o g P)$ ， $P$ 是选区的像素数量。

求解：

在初始化的时候，我们有 $i$ 组数据，对于输入图像数据 $F_i$ ，我们期望输出的响应为 $G_i$ 。
通过求解以下最小化问题，“训练” 出我们期望的相关核 $H$ ： $\min_{H^*} \sum^{}_{i} | F_i \odot H^* - G_i |^2 \tag{3}$

这叫做最小化平方误差和（Sum of Squared Error，SSE），文章的标题和跟踪器的名字由此而来。

作者在文章的附录中给出了求解公式。作者表示这是一个凸的，使偏导为 $0$ 得到求解公式： $H^* = \frac{\sum_i G_i \odot F_i^*} {\sum_i F_i \odot F_i^*} \tag{4}$

这 $i$ 组数据怎么来？代码中 $i = 128$ ，在初始化的时候，对输入图像 $f$ 做 $128$ 次随机仿射变换（旋转、拉伸等）得到一系列图：

在这里插入图片描述

每张图片输出响应 $G_i$ 不变，依旧是用（图1）那个 $g$ 的傅里叶逆变换 $G_i$ 。将 $F_i$ ， $G_i$ 代入式 (4) 求得 $H$ 。

不做仿射变换，只用一张原图也可以，但是这样得到的滤波器太精确，会过拟合这幅图像，当应用到新图像 (下一帧) 的时候容易跟踪失败。
这种对数据增强然后求平均的方法，可以产生一个更具泛化能力的滤波器。
（对弱分类器的输出进行平均，从而产生一个强得多的分类器）。

另外，我们还对图片加入了白噪声 $\epsilon$ ，具有正则化的效果。可以得到具有更好的噪声容忍能力的滤波器。
在两个地方加，一个是图片预处理的时候加，一个是在式 (4) 中加： $F_i \odot F_i^* +\epsilon$ 。

初始化完毕后，就得到了滤波器模板 $H$ 。

在线更新：（选区框）

在跟踪问题中，目标不总是居中的。

例如当下一帧数据来到的时候，我们的选区（目标框）还处于原来的位置，但是里面的目标已经移动了。

在 $f$ 中峰值会随着目标的移动而移动。用目前的滤波器 $H$ 做相关时，得到的响应也会发生变化：

在这里插入图片描述

通过计算响应峰值点的相对位移，来更新跟踪框的坐标，使目标仍处于跟踪框中心。

值得注意的是，目标框的大小没有得到更新，这也是 MOSSE 算法的不足之一。

在线更新：（滤波器）

在跟踪的过程中，目标通常会发生旋转、缩放、姿态、光照的变化，甚至外观发生非刚性形变，所以滤波器需要随之适应和更新。

记 $H_1 = \sum_i G_i \odot F_i^*$ ， $H_2 = \sum_i F_i \odot F_i^*$
则式 (4) 简写为： $H^* = \frac{H_1}{H_2}$

下一帧数据 $F_{n}$ 来到的时候，通过以下式子更新 $H$ ： $H_1^{new} = \textcolor{red}{(1-\eta)}\;H_1 + \textcolor{red}{ \eta }\; G \odot F_{n}^* \\[1em] H_2^{new} = \textcolor{red}{(1-\eta)}\;H_2 + \textcolor{red}{ \eta }\; F_{n} \odot F_{n}^*$
即：
$H^* = \frac{ \textcolor{red}{(1-\eta)}\;H_1 + \textcolor{red}{ \eta }\; G \odot F_{n}^*} {\textcolor{red}{(1-\eta)}\;H_2 + \textcolor{red}{ \eta }\; F_{n} \odot F_{n}^*}$

$\eta$ 称为学习率，实际中取 $\eta = 0.125$ 效果较好。

得到新的过滤器和新的选区，就可以进行下一帧的跟踪了。不断迭代这个过程。

失败判定与PSR：

我们用 PSR（Peak to Sidelobe Ratio）度量响应尖峰的强度。
对于相关输出 $g$ ，我们找出峰值点 $g_{\text{max}}$ ，以峰值点为中心建立 $11\times 11$ 的矩形框。
计算这个矩形区域的均值 $\mu_{\text{s1}}$ 和标准差 $\sigma_{\text{s1}}$ ，则 $\text{PSR} = \frac{g_{\text{max}} - \mu_{\text{s1}}}{\sigma_{\text{s1}}}$