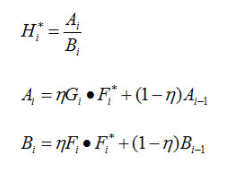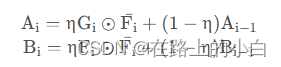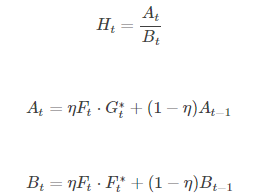引言

  MOSSE是在Visual Object Tracking using Adaptive Correlation Filters这篇文章中提出来的，MOSSE的全称是Minimum Output Sum of Squared Error，令平方误差和最小来计算得到滤波器。

算法流程

  相关滤波很容易理解，一帧图像经过相关运算（滤波器）之后得到的响应图中，响应最大的位置就是目标所在的位置。这个相关计算的模板也就是滤波器，它滤除了和它不相关的内容。

相关运算和卷积运算

  相关Correlation和卷积Convolution有着紧密的联系。以一维的情况考虑。$f[n]$是原始序列，$h[n]$是滤波器，在它们都是实数的情况下，相关运算结果$g[n]$可以表示为：
$$g[n]=\sum _{\tau =-\infty }^{\infty }f[\tau ]h[n+\tau ]$$
  两者卷积的结果为：
$$f[n]\ast h[n]=\sum _{\tau =-\infty }^{\infty }f[\tau ]h[\tau -n]$$
  可以观察到，相关和卷积的计算非常相似，我们如果让$f[n]$与$h[-n]$卷积，那就能得到相关计算的结果了。有人可能会问了$h[n]$可以理解，但是$h[-n]$的话索引就小于0了，是什么呀？我们先不管这个，先定性地再理解一下卷积和相关运算的区别。在一维的情况下，相关运算就像是把一条线段在另一条线段上拖动，每次两条线段重合区域的长度就是运算结果；卷积运算则是仅仅多了把一条线段反转的步骤，同样也是拖动然后看重合的长度。这样我们就好理解了，这个$h[-n]$中的负号只是起到了序列前后反转的作用。
$$g[n]=f[n]\ast h[-n]$$
  那么我们就可以把相关运算表示成上面的卷积运算。很多情况下，如果$h[n]$是一个对称的序列，那么卷积和相关运算得到的结果就是一样的。
  为了简化计算，时域的卷积转化为频域的乘积，我们用DFT可以由$f[n]$计算得到$F[k]$，下面是$h[n]$的DFT：
$$H[k]=\sum _{n=0}^{N-1}h[n]e^{-j2\pi \frac{kn}{N}}$$
  而$h[-n]$经过DFT之后得到的是什么呢？因为一个序列就只有0到N-1的索引，这负的索引是什么呢？为此我又回顾了一遍DFT，我看的主要是奥本海姆的《离散时间信号处理》。书里讲的DFT和DFS非常像，确实非常像！我自己的理解是：DFS和传统意义的傅立叶变换更接近，它实现的是离散周期序列与离散周期序列之间的转换（因为存在“周期对离散”，“非周期对连续”这样的对应关系）。而DFT则是截取了DFS的一个周期的序列来表示，可以说只是一种表示方法，在处理的时候要注意它固有的周期性。

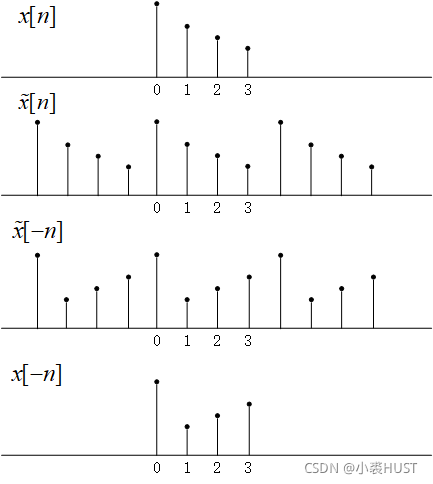
  举个例子，$x[n]$是长度为4的序列，$\tilde{x}[n]$是周期延拓后的序列，$\tilde{x}[-n]$是翻转后的序列，$x[-n]$是从翻转后的序列中提取一个周期的序列。
$$\sum _{n=0}^{N-1}h[-n]e^{-j2\pi \frac{kn}{N}}=h[0]+\sum _{n=1}^{N-1}h[N-n]e^{-j2\pi \frac{kn}{N}}$$
  令$l=N-n$，则$n=N-l$，代入上式得：
$$h[0]+\sum _{l=1}^{N-1}h[l]e^{-j2\pi \frac{k(N-l)}{N}}=h[0]+\sum _{l=1}^{N-1}h[l]e^{j2\pi \frac{kl}{N}}=\sum _{l=0}^{N-1}h[l]e^{j2\pi \frac{kl}{N}}=H^{\ast }[k]$$
  到这里我们就有了$f[n]$和$h[-n]$的DFT，它们俩的卷积可以用乘积表示，我们把$g[n]$的DFT结果记为$G[k]$，则：
$$G[k]=F[k]\odot H^{\ast }[k]$$

MOSSE算法

  上面的式子再推广到二维的情况也一样是成立的，$\odot$表示二维矩阵$F$和$H^{\ast }$的对应元素相乘。
$$G=F\odot H^{\ast }$$
  我们的目标是求$H^{\ast }$，$F$是输入的图像，$G$是输出的响应。这个响应需要我们自己设计。目标经过滤波器后，目标所在位置的响应最大，当目标在图像中央时，我们可以把这个响应设定为峰值位置在图像中央的二维高斯函数。
  如果只有一幅训练图片的话，这就已经能算出来了，$H^{\ast }=\frac{G}{F}$（这里的除法指的是对应元素相除），但是一般不只一幅图，所以要求一个最优的$H^{\ast }$。为此论文中提出的准则是使每幅图计算的结果和高斯模板之间的平方误差之和最小，用公式表示就是：
$$\underset{H^{\ast }}{\min }\sum _i{\left|F_i\odot H^{\ast }-G_i\right|}^2$$
  接下来就是想办法求这个最优化问题了，可以看到它类似一个一元二次函数，但这里又都是复数运算，所以还是有点不同。求解$H^{\ast }$可以分解为求解它的每一个元素。对于$w$行，$v$列的元素，有：
$$\underset{H^{\ast }}{\min }\sum _i{\left|F_{iwv}\odot H_{wv}^{\ast }-G_{iwv}\right|}^2$$
  这就是标量运算了，我们先看$i=1$的情况。
$$\begin{array}{l}\underset{H^{\ast }}{\min }\left|F_{wv}{H^{\ast }}_{wv}-G_{wv}\right|\\ =\underset{H^{\ast }}{\min }\left(F_{wv}{H^{\ast }}_{wv}-G_{wv}\right){\left(F_{wv}{H^{\ast }}_{wv}-G_{wv}\right)}^{\ast }\\ =\underset{H^{\ast }}{\min }{F}_{wv}{F_{wv}}^{\ast }{H}_{wv}{H^{\ast }}_{wv}-G_{wv}{F_{wv}}^{\ast }{H}_{wv}-{G_{wv}}^{\ast }{F}_{wv}{H^{\ast }}_{wv}-G_{wv}{G^{\ast }}_{wv}\end{array}$$
  求极值要涉及对复数的变量求导，有人提出了Wirtinger导数，其中$z=x+jy$，
$$\begin{gathered} \frac{\partial }{\partial z}=\frac{1}{2}\left[\frac{\partial }{\partial x}-j\frac{\partial }{\partial y}\right] \\ \frac{\partial }{\partial z^{\ast }}=\frac{1}{2}\left[\frac{\partial }{\partial x}+j\frac{\partial }{\partial y}\right] \end{gathered}$$
  根据上面的式子可以计算得到：
$$\frac{\partial }{\partial z}{z}^{\ast }=\frac{\partial }{\partial z^{\ast }}z=0$$
  据此可以知道$H_{wv}$在对$H_{wv}^{\ast }$求导的时候可以看作常数。因此对目标函数求导，并令导数为0可得：
$$\begin{array}{l}\frac{\partial }{\partial H_{wv}^{\ast }}\left(F_{wv}{F_{wv}}^{\ast }{H}_{wv}{H^{\ast }}_{wv}-G_{wv}{F_{wv}}^{\ast }{H}_{wv}-{G_{wv}}^{\ast }{F}_{wv}{H^{\ast }}_{wv}-G_{wv}{G^{\ast }}_{wv}\right)\\ =F_{wv}{F_{wv}}^{\ast }{H}_{wv}-{G_{wv}}^{\ast }{F}_{wv}=0\end{array}$$
$$H_{wv}=\frac{{G_{wv}}^{\ast }{F}_{wv}}{F_{wv}{F_{wv}}^{\ast }},{H_{wv}}^{\ast }=\frac{G_{wv}{F_{wv}}^{\ast }}{F_{wv}{F_{wv}}^{\ast }}$$
  再推广到$i>1$的情况：
$$H^{\ast }=\frac{{\sum }_i{G}_i\odot {F_i}^{\ast }}{{\sum }_i{F}_i\odot {F_i}^{\ast }}$$
  最后引入了学习率$\eta$来更新$H^{\ast }$：
$$\begin{array}{l}{H_n}^{\ast }=\frac{A_n}{B_n}\\ A_n=\eta G_n\odot {F_n}^{\ast }+(1-\eta )A_{n-1}\\ B_n=\eta F_n\odot {F_n}^{\ast }+(1-\eta )B_{n-1}\end{array}$$
  其中$n=1,2,3...$代表测试图片的帧数。$A_0={\sum }_i{G}_i\odot {F_i}^{\ast }$,$B_0={\sum }_i{F}_i\odot {F_i}^{\ast }$，实践中发现，$\eta =0.125$效果较好。