汉诺塔递归的c语言实现(递归)

对于递归来讲, 汉诺塔实际是经典到不能再经典的例子了, 每个数据结构的教材对会提到.

但是到最后只给出一段类似下面的一段代码:

#include<stdio.h>void move(int n,char a,char b,char c)
{if(n==1)printf("\t%c->%c\n",a,c);    //当n只有1个的时候直接从a移动到c else{   move(n-1,a,c,b);            //把a的n-1个盘子通过c移动到b printf("\t%c->%c\n",a,c);   //把a的最后1个盘(最大的盘)移动到c move(n-1,b,a,c);            //吧b上面的n-1个盘通过a移动到c }   
}main()
{int n;printf("请输入要移动的块数："); scanf("%d",&n);move(n,'a','b','c');
}

这段代码用来学习递归思想是足够的, 也能大概上了解到移动汉诺塔的步骤.

但是我说, 这段代码没有体会出汉诺塔的本质, 也没有办法验证.

下面我会敲出能体现出汉诺塔本质的递归代码. 并能根据输出每1个步汉诺塔的状态, 并且验证正确性.

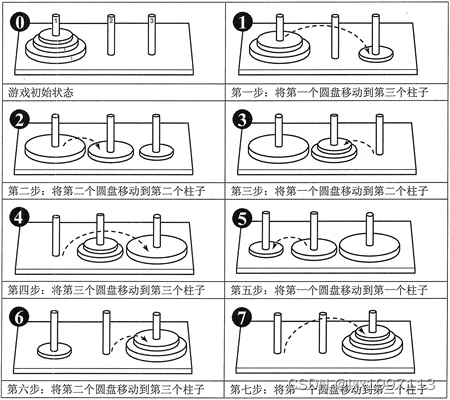
1. 什么是汉诺塔

下面的定义摘自维基百科:

有三根杆子A，B，C。A杆上有N个(N>1)穿孔圆盘，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至C杆：

每次只能移动一个圆盘；
大盘不能叠在小盘上面。

配图:

2. 汉诺塔的本质是3个栈

维基的定义只简单提到了汉诺塔的规则, 但是并没有揭示它的本质. 下面我们来分析它的本质.

1.每次只能移动1个盘:

也就说不能两个盘一齐移动, 必须按顺序1个1个套在柱子上, 而且只能从柱子的上方套入, 也能只能从柱子的上方取出.

这明显就是1个先进后出的线性结构了, 因为出入口只有1个啊, 柱子的下方是不能放入和取出盘子的.

先进后出的线性结构就是栈了, 套入柱子和取出盘子就是对应的压栈和出栈动作. 如果读者之前没有了解过栈的话, 个人建议先去了解下栈, 然后再往下看.

2. 大盘不能套在小盘上面

代表这3个栈中, 如果不是空栈, 那么压栈的元素必须比栈顶元素小, 然后才允许压栈. 这就保证栈里面的元素是从小到大排序的.

总结: 汉诺塔的本质就是3个栈, 而且压栈的元素必须比栈顶元素(如果存在)小.

3. 汉诺塔的解题思路及递归原理

好, 现在开始讲解汉诺塔的解题思路.

假如A塔有n个盘子, 大小从大(底部) 到小(顶部)排列, B塔和C塔都是空塔.

如下图:

好了那么到底如何把这个n个盘子移动到C塔呢?

3.1 假如n=1 也就是说A塔只有1个盘子的情况下, 直接将1个盘子移动到c塔

那么我们写1个函数move()

执行move(A,C) 就是把A里唯一1个盘子移动到C

当然这里先不管这个函数具体是如何实现的.

但是可看出, 这个过程是不需要借助B塔中转的.

3.2 n>1的情况分析, hanoi_m(A,B,C,n) 函数

但是n>1呢? 上面的move函数就行不同了, 所以我们需要1个新的函数 hanoi_m()

hanoi_m(A, B, C, n) 函数意思就是把n个盘子从A借助B移动到C.

这里也先不管这个函数是如何具体如何实现, 知道它的参数意义和目地就ok了.

我上篇文章讲过, 递归的条件之一就是令数据规模不断地减少, 也就是假如1个函数f(n) 是递归函数, 则必须要找出f(n) 与f(n-1)关系, 也就是说把求f(n) 转化为求f(n-1), 然后再转化为求f(n-2), 最终f(1)就是出口.

那么这里的hanoi_m(x,x,x,1) 是什么呢? 就是上面的move()函数了, 也就说出口找到了.

但是hanoi_m(x,x,x,n) 与 hanoi_m(x,x,x, n-1) 的关系还不知道, 这就是汉诺塔递归函数的精髓了!

下面步骤就是讲解这个n 与 n-1的关系.

关键的一点: 假如要将n-1个盘子放到C塔, 如果c塔是非空的话, 那么c塔的盘子都必须比n-1大, 否则按照规则是不能放入的!

所以最大的盘子必须比它小的所有盘子先放入C塔.

1.但是如果要将最大的盘子从A塔移动到C塔, 那么C塔必须是空的, 不让放不下

2.而且最大的盘子必须在A塔的最上面, 也就是说A塔只有1个最大的盘子.

3.所以其他盘子都必须在B塔上,

理解好这个那么问题就不大了

下面是详细步骤

3.3 第一步, 将A上面的n-1个盘子借助C塔移动到B塔. hanoi(A,C,B,n-1)

这个过程用函数来表示就是hanoi_m(A,C,B,n-1)啊, 理解这一步也十分关键:

如图:

至于这个过程具体如何实现, 这里也不用去管, 只有1点是明确的, 只要n-1>1 那么这个过程肯定需要C塔来中转, 而且肯定可以化为求 hanoi_m(x,x,x, n-2).

假如n-1=1? 就直接move(A,B)就ok了, 这就是出口啊.

3.4 第二步, 将A上面的最后的(最大的)盘子移动到C塔 move(A,C)

因为现在A塔了只有1个最大盘子n了啊, 所以无需借助B塔, 直接move(A,C)搞定

如下图:

注意现在还没完成哦

3.4 第三步, 将B上面的所有盘子(n-1)个盘子借助A塔移动到C塔 hanoi(B,A,C,n-1)

因为C塔的盘子比B塔的所有盘子都大, 所以是可以忽略掉C盘的那个最大的盘子的, 理解这个也很重要啊.

这个函数实现就是 hanoi(B,A,C,n-1)

如图:

搞掂完成了...

3.5 总结及伪算法:

经过上面的图解, 我们知道hanoi(n) 与hanoi(n-1)的关系了, 可以分成三步啊

伪算法就是:

hanoi_m(A,B,C,n){if (n==0){move(A,C);}hanoi_m(A,C,B,n-1);move(A,C);hanoi_m(B,A,C,n-1);
}

看看这个函数, 自己调用了自己, 而且规模不断在减少, 还有1个明确的出口, 标准的递归函数啊.

再看看本文开始那个函数, 是不是能理解了

然而真正的代码实现没那么简单, 但是起码逻辑已经清楚了.

4. 1个静态栈(数组内核)的容器的c语言代码实现

假设我们可以用类似下面的代码来定义3个栈, 和调用压栈和出栈函数, 就很方便了.

//declare a stucks
stuck A = new stuck;//push
A->push(1);  //push element int "1" into the stuck//pop
int i;
A->pop(&i) //pop the top element, and assign the value to variable i

咋一看不是c++的代码吗?, 的确c语言不能实现面向对象的类.

但是利用c语言里的结构体和函数指针, 也可以实现类似上面代码的功能.

用c语言写1个静态栈容器并不是很简单, 可以说远比汉诺塔的函数复杂, 具体的代码我就不讲解了. 有兴趣的可以参考我之前的文章, 有1个动态栈(链表内核)的c语言代码例子讲解.

但是静态栈的原理远比动态栈复杂.

下面我只会介绍下头文件的函数, 具体当面我会作为附件, 有兴趣的可以下载:

#include "bool_me.h"
#ifndef __ARRSTUCK1_H_
#define __ARRSTUCK1_H_struct arrstuck1{int * pArr;  //address of array (int type)int arrlen;  //the maxlen of th arrayint top; //index of the top + 1int buttom; //index of buttom , default is 0const char * stname; //name of stuck, haha ,used to print the log to logfileint (* len)(struct arrstuck1 *);   //get the lengthint (* TopVal)(struct arrstuck1 *);  //get the top valueint (* ButtomVal)(struct arrstuck1 *);  //get the top valueBOOL (* is_empty)(struct arrstuck1 *);BOOL (* is_full)(struct arrstuck1 *);BOOL (* push)(struct arrstuck1 *, int);   //push an element to the stuckBOOL (* pop)(struct arrstuck1 *, int *); //pop the topelemnt to the stuckvoid (* print)(struct arrstuck1 *); //print from buttom to topvoid (* print_from_top)(struct arrstuck1 *); //print from top to buttomvoid (* clean)(struct arrstuck1 *); //remove all elementsBOOL is_inited; //judge whether the arraystuck is initialed};typedef struct arrstuck1 INT_STUCK;//initailINT_STUCK * ast_int_new();//freeBOOL ast_free(INT_STUCK *);#endif /* __ARRSTUCK1_H_ */

上面就是静态栈容器 INT_STUCK(定义别名) 的头文件, 它只可以存放int类型的元素.

我们只需要关系几个关键的成员函数.

1. push() 函数就是压栈啦

2. pop() 函数出栈

3. print() 打印栈里面的所有元素, 用于验证算法的正确性啦.

4. len() 栈里面元素的个数.

5. ast_int_new5. in() 初始化函数, 不初始化没法用的.

其他的可以看注释了.

具体的函数定义请下载来看:

bool_me.h : 定义BOOL 类型

basefuncs.h

basefuncs.c :输出错误和日志的基本函数

arrstuck1.h

arrstuck1.c 静态栈容器

因为这篇文章的注意目地是分析汉诺塔的递归函数嘛..

5. 汉诺塔递归c语言实现

好了, 到此为止, 准备动作做完了, 下面开始分析和编写汉诺塔的函数

5.1 定义单个汉诺塔类型及其初始化函数

上面讲过了, 汉诺塔的本质就是栈,, 所以汉诺塔类型就是栈啦, 用typedef 函数起个别名就ok了

利用函数指针可以为函数起别名

代码如下:

typedef INT_STUCK HANOITOWER;
static HANOITOWER * (* hanoi_new)() = ast_int_new;

这样就定义了1个"新"的类型 HANOITOWER, 和初始化函数 hanoi_new()

5.2 汉诺塔放盘子函数hanoi_push

实际上就是栈的压栈函数, 当然, 这里要判断入栈的值必须比栈顶小!

代码如下:

BOOL hanoi_push(HANOITOWER * pIst, int val){if (TRUE != pIst->is_empty(pIst) && val >= pIst->TopVal(pIst)){printf("val is greater than top!\n");return FALSE;}pIst->push(pIst, val);return TRUE;
}

5.3 定义3个汉诺塔栈 A,B,C 并往A里面放4个盘子

有了上面的函数, 就可以初始化3个塔, 并往A塔放4个盘子了, 当然B,C塔必须是空塔(空栈)

当然放几个盘子自己定义, 建议不要放太多啦, 移动盘子动作增长速度很恐怖的. 反正我的渣机子算24个盘子要5分钟才出结果

代码如下:

        HANOITOWER * pTa = hanoi_new();pTa->stname = "TowerA";HANOITOWER * pTb = hanoi_new();pTb->stname = "TowerB";HANOITOWER * pTc = hanoi_new();pTc->stname = "TowerC";int i;for (i=4; i >= 1; i--){hanoi_push(pTa, i);}

5.4 从非空汉诺塔取盘子函数 hanoi_pop

没错, 本质上就是出栈函数啊, 拿出栈顶元素(用于放到别的栈)

所以要接受1个 int 类型的指针参数, 用于存放和取出这个栈顶啊.

代码如下:

BOOL hanoi_pop(HANOITOWER * pIst, int * pVal){if (TRUE == pIst->is_empty(pIst)){printf("fail to pop as the stuck is empty!\n");return FALSE;}pIst->pop(pIst, pVal);return TRUE;
}

5.5 把1个盘子从1个塔移动到另1个塔函数 hanoi_move

没错, 实际上我们操作汉诺塔, 不会单独地取盘子和放盘子, 而是把1个塔的顶部盘子拿出来放到另1个塔的顶部!

所以这个函数Hanoi_move 的参数有两个栈, T_from 和 T_to

实际上是分解上出栈和压栈函数

从T_from出栈并获得出栈的元素(盘子), 然后把这个元素压栈到T_to中.

代码如下:

BOOL hanoi_move(HANOITOWER * pIst_from, INT_STUCK * pIst_to){int val;if (TRUE == hanoi_pop(pIst_from, &val)){if (TRUE == hanoi_push(pIst_to, val)){//mark log to filesprintf(hanoi_move_str, "\nmove %d from %s to %s\n", val, pIst_from->stname, pIst_to->stname);base_log(hanoi_move_str, HANOI_OP_FILE, "a");base_log_intarr(pIst_from->stname, pIst_from->pArr, pIst_from->len(pIst_from), HANOI_OP_FILE, "a");base_log_intarr(pIst_to->stname, pIst_to->pArr, pIst_to->len(pIst_to), HANOI_OP_FILE, "a");return TRUE;}}return FALSE;
}

见到, 如果移动成功, 会把移动盘子的信息(从哪里移动到哪, 移动哪个元素) 记录在日志文件, 而且记录每1个移动步骤后, 两个塔里面的元素状态.

其中hanoi_move_str 是外部定义公共变量

5.6 输出单个塔里面的元素函数 hanoi_print

实际上就是输出栈里面的所有元素啦, 用于验证嘛..

void hanoi_print(HANOITOWER * pIst){pIst->print(pIst);
}

5.7 解题递归函数 hanoi_m

原理和伪算法上面都讲过了啦, 不是吗? 而且有了上面的代码准备, 现在写这个递归函数就十分简单了.

代码如下:

int hanoi_m(HANOITOWER * pfrom, HANOITOWER * pmid, HANOITOWER *pto, int count){if (count == 1){hanoi_move(pfrom, pto);return 0;}hanoi_m(pfrom,pto,pmid,count-1);hanoi_move(pfrom, pto);hanoi_m(pmid,pfrom,pto,count-1);return 0;
}

6. 测试这个汉诺塔代码

好了, 所有函数都写好了, 就写1个测试程序验证啊, n先设为4嘛, 不让日志太长了..

代码如下:

int hanoi1(){HANOITOWER * pTa = hanoi_new();pTa->stname = "TowerA";HANOITOWER * pTb = hanoi_new();pTb->stname = "TowerB";HANOITOWER * pTc = hanoi_new();pTc->stname = "TowerC";hanoi_move_str = (char *)malloc(sizeof(char) * 50);int i;for (i=4; i >= 1; i--){hanoi_push(pTa, i);}printf("before move\n");printf("tower A is below\n");hanoi_print(pTa);printf("tower B is below\n");hanoi_print(pTb);printf("\ntower C is below\n");hanoi_print(pTc);base_log("start to move\n", HANOI_OP_FILE, "w");hanoi_m(pTa, pTb, pTc, pTa->len(pTa));printf("\nafter move\n");printf("tower A is below\n");hanoi_print(pTa);printf("\ntower B is below\n");hanoi_print(pTb);printf("\ntower C is below\n");hanoi_print(pTc);ast_free(pTa);ast_free(pTb);ast_free(pTc);free(hanoi_move_str);printf("hanoi_new done\n");return 0;
}

注意我先移动前先输出3个塔的元素, 移动后再输出1次, 就可以验证了嘛..

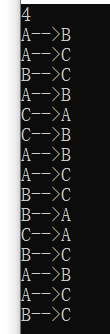
输出: 注意看栈的输出元素.

我上面是不是说了每1次移动我都会记录在日志文件中:

打开来看看就可以知道每一次移动的作用和意义了, 能加深理解哦:

gateman@TFPC c_start $ cat ~/tmp/HANIO_OP_FILE.log 
start to movemove 1 from TowerA to TowerB
TowerA: 4, 3, 2
TowerB: 1move 2 from TowerA to TowerC
TowerA: 4, 3
TowerC: 2move 1 from TowerB to TowerC
TowerB: blank array!
TowerC: 2, 1move 3 from TowerA to TowerB
TowerA: 4
TowerB: 3move 1 from TowerC to TowerA
TowerC: 2
TowerA: 4, 1move 2 from TowerC to TowerB
TowerC: blank array!
TowerB: 3, 2move 1 from TowerA to TowerB
TowerA: 4
TowerB: 3, 2, 1move 4 from TowerA to TowerC
TowerA: blank array!
TowerC: 4move 1 from TowerB to TowerC
TowerB: 3, 2
TowerC: 4, 1move 2 from TowerB to TowerA
TowerB: 3
TowerA: 2move 1 from TowerC to TowerA
TowerC: 4
TowerA: 2, 1move 3 from TowerB to TowerC
TowerB: blank array!
TowerC: 4, 3move 1 from TowerA to TowerB
TowerA: 2
TowerB: 1move 2 from TowerA to TowerC
TowerA: blank array!
TowerC: 4, 3, 2move 1 from TowerB to TowerC
TowerB: blank array!
TowerC: 4, 3, 2, 1

看到n=4 的话执行了 15次move动作

注意n不要设成太大啊, 不然这个日志会有成千上万行的啊!

分析一下, 从n =1 到n =5 的5个样本

move分别执行了

1 3 7 15 31 .... (2-1,4-1,8-1,16-1

也就是随着n增长, move执行次数= 2^n-1

可以看出, 随着n的增长, move的执行次数增长是几何级数的节奏啊!! 所以从时间复杂度O(2^n)来看, 这个递归函数是非常糟糕的. 但是毕竟容易理解和易于实现啊.

到底有多糟糕, 我将n设为24, 执行了8分钟才出结果,

move执行了, 1677多万次

日志文件6700多万行, 大小高达1.6 GB, 真是瞎了我的狗眼.

最后附上这个汉诺塔程序的代码:

和上面的静态栈文件1齐编译就能执行了