哈希树的理论基础

质数分辨定律

这个定理可以简单的表述为：n个不同的质数可以“分辨”的连续整数的个数和他们的乘积相等。“分辨”就是指这些连续的整数不可能有完全相同的余数序列。这个为哈希树的分辨方式奠定了理论基础。

显然，这个定理的一个特殊情况就是为从2起的连续质数。我们可以记为前个连续质数的乘积。连续10个质数就可以分辨大约个数，已经超过计算机中常用整数（32bit）的表达范围。

而按照目前的CPU水平，100次取余的整数除法操作几乎不算什么难事。在实际应用中，整体的操作速度往往取决于节点将关键字装载内存的次数和时间。一般来说，装载的时间是由关键字的大小和硬件来决定的；在相同类型关键字和相同硬件条件下，实际的整体操作时间就主要取决于装载的次数。他们之间是一个成正比的关系。

余数分辨定理

这个定理可以简单的表述为：n个不同的数可以“分辨”的连续整数的个数不超过他们的最小公倍数。超过这个范围就意味着冲突的概率会增加。定理1是定理2的一个特例。

哈希树简介

从2起的连续质数，连续10个质数就可以分辨大约M(10) =2*3*5*7*11*13*17*19*23*29= 6464693230 个数（64亿），已经超过计算机中常用整数（32bit）的表达范围（int的范围为正负20个亿）。连续100个质数就可以分辨大约M(100) = 4.711930 乘以10的219次方。

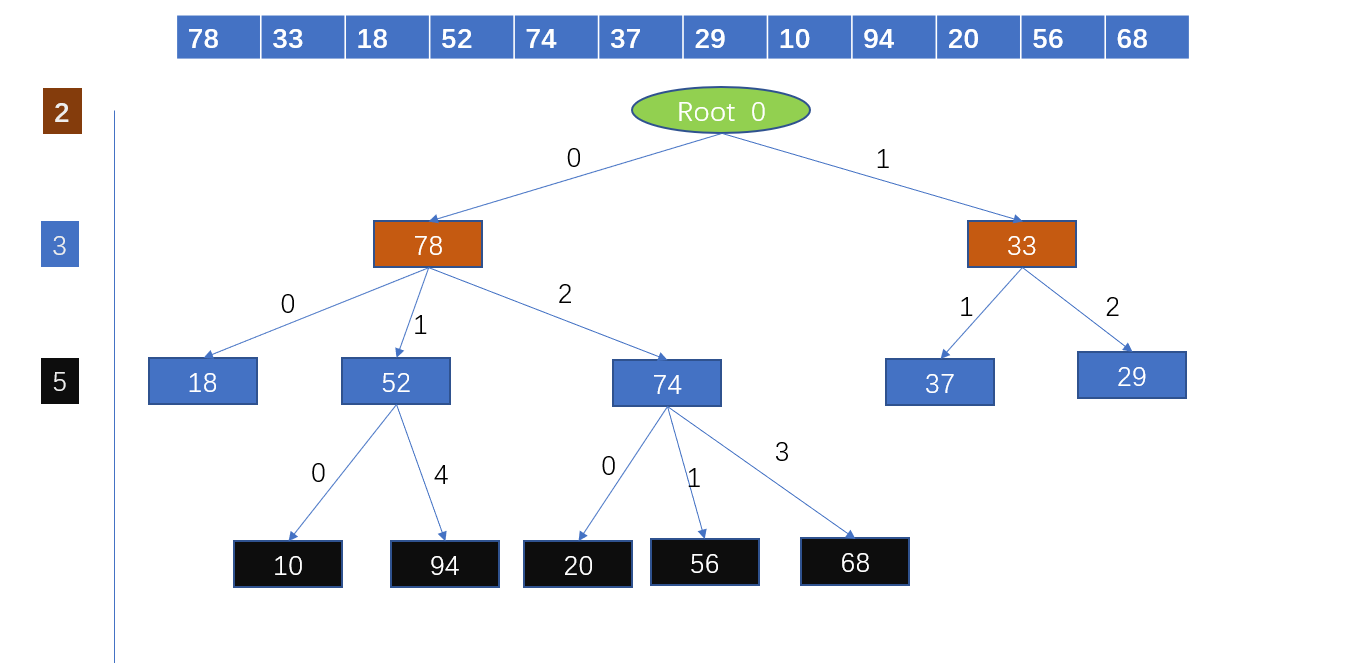
我们选择质数分辨算法来建立一颗哈希树。选择从2开始的连续质数来建立一个十层的哈希树（因为已经超过了计算机中常用整数的表达范围）。第一层节点为根节点，根节点下有2个节点；第二层的每个节点下有3个节点；依此类推，即每层节点的子节点数目为连续的质数。到了第十层，每个节点下有29个节点。

同一结点中的子结点，从左到右代表不同的余数结果。
例如：第二层结点下有三个子节点。那么从左到右分别代表：除3余0，除3余1，除3余2.
对质数进行取余操作得到的余数决定了处理的路径。

也就是说如果有21亿个数字的话，我们查找的哪怕是最底层的也仅仅需要计算10次就能找到对应的数字。

所以hash树是一棵为查找而生的树。

查找

哈希树的节点查找过程和节点插入过程类似，就是对关键字用质数序列取余，根据余数确定下一节点的分叉路径，直到找到目标节点。
如上图，最小”哈希树(HashTree)在从4G个对象中找出所匹配的对象，比较次数不超过10次。也就是说：最多属于O(10)。在实际应用中，调整了质数的范围，使得比较次数一般不超过5次。也就是说：最多属于O(5)。因此可以根据自身需要在时间和空间上寻求一个平衡点。

删除

哈希树的节点删除过程也很简单，哈希树在删除的时候，并不做任何结构调整。
只是先查到到要删除的节点，然后把此节点的“占位标记”置为false即可（即表示此节点为空节点，但并不进行物理删除）。

优点

结构简单

从哈希树的结构来说，非常的简单。每层节点的子节点个数为连续的质数。子节点可以随时创建。因此哈希树的结构是动态的，也不像某些哈希算法那样需要长时间的初始化过程。哈希树也没有必要为不存在的关键字提前分配空间。
需要注意的是哈希树是一个单向增加的结构，即随着所需要存储的数据量增加而增大。即使数据量减少到原来的数量，但是哈希树的总节点数不会减少。这样做的目的是为了避免结构的调整带来的额外消耗。

查找迅速

从算法过程我们可以看出，对于整数，哈希树层级最多能增加到10。因此最多只需要十次取余和比较操作，就可以知道这个对象是否存在。这个在算法逻辑上决定了哈希树的优越性。
一般的树状结构，往往随着层次和层次中节点数的增加而导致更多的比较操作。操作次数可以说无法准确确定上限。而哈希树的查找次数和元素个数没有关系。如果元素的连续关键字总个数在计算机的整数（32bit）所能表达的最大范围内，那么比较次数就最多不会超过10次，通常低于这个数值。

结构不变

从删除算法中可以看出，哈希树在删除的时候，并不做任何结构调整。这个也是它的一个非常好的优点。常规树结构在增加元素和删除元素的时候都要做一定的结构调整，否则他们将可能退化为链表结构，而导致查找效率的降低。哈希树采取的是一种“见缝插针”的算法，从来不用担心退化的问题，也不必为优化结构而采取额外的操作，因此大大节约了操作时间。

缺点

非排序性

哈希树不支持排序，没有顺序特性。如果在此基础上不做任何改进的话并试图通过遍历来实现排序，那么操作效率将远远低于其他类型的数据结构。

哈希树的java实现

节点

package datastructure.tree.hashtree;import java.util.Arrays;public class Node {//node的下一层的节点public Node[] next;//节点的值public int value;//节点是否已被删除public boolean isDel;public Node(int value,int nextNum){this.value=value;this.next=new Node[nextNum];this.isDel=false;}@Overridepublic String toString() {return "Node [next=" + Arrays.toString(next) + ", value=" + value + ", isDel=" + isDel + "]";}}

哈希树

如何操作都在注释中

基本思路就是先处理root，然后处理下一层的节点，然后再跳到下一层去

package datastructure.tree.hashtree;public class HashTree {public static final int[] primeNumber=new int[]{2,3,5,7,11,13,17,19,23,29};//连续11个质数能表示6464693230个数字Node root;/**HashTree初始化* 对根节点的值设置成0，但是被删除的节点*/public HashTree(){root=new Node(0, primeNumber[0]);root.isDel=true;}/** 在HashTree中插入一个节点* @param value 节点的值*/public void insertNode(int value){//如果HashTree中已经有这个节点，就不插入if(searchNode(value)){return;}		//排除root节点被删除或者初始化的情况if(root.isDel==true){root.value=value;root.isDel=false;return;}//层级，在每一层，primeNumber[level]为下一层的节点数int level=0;				Node nowNode=root;while(true){//得到下个节点的位置（因为已经考虑了root，可以直接考虑下一层的情况）int index=value%(primeNumber[level]);			if(nowNode.next[index]==null){//在第n层，primeNumber[level]为n+1层的节点数，primeNumber[level+1]为n+2层的节点数//在第n层nowNode.next[index]为第n+1层的节点，它的next的数量为n+2层的节点数nowNode.next[index]=new Node(value, primeNumber[level+1]);break;}//将被删除的节点更新为当前值if(nowNode.next[index].isDel==true){nowNode.next[index].value=value;nowNode.next[index].isDel=false;break;}//到下一个对应节点nowNode=nowNode.next[index];level++;			}	}/**在HashTree中查询节点是否存在* @param value 节点的值* @return 存在，返回true  不存在，返回false*/public boolean searchNode(int value){//考虑root是查找节点if(root.value==value&&root.isDel==false){return true;}//层级，在每一层，primeNumber[level]为下一层的节点数int level=0;				Node nowNode=root;while(true){//得到下个节点的位置（因为已经考虑了root，可以直接考虑下一层的情况）int index=value%(primeNumber[level]);//如果对应节点为空，直接返回falseif(nowNode.next[index]==null){return false;}//如果对应节点没有被删除而且值相同，直接返回falseif(nowNode.next[index].isDel==false&&nowNode.next[index].value==value){return true;}//到下一个对应节点nowNode=nowNode.next[index];level++;			}	}/**在HashTree中删除值为value的节点* @param value 节点的值* @return 如果删除成功，返回true   如果HashTree中没有这个节点或者已经被删除，返回false*/public boolean deleteNode(int value){//考虑root是被删除节点if(root.value==value&&root.isDel==false){root.isDel=true;return true;}//层级，在每一层，primeNumber[level]为下一层的节点数int level=0;				Node nowNode=root;while(true){//得到下个节点的位置（因为已经考虑了root，可以直接考虑下一层的情况）int index=value%(primeNumber[level]);//如果对应节点为空，直接返回falseif(nowNode.next[index]==null){return false;}//如果对应节点没有被删除而且值相同，进行删除，返回trueif(nowNode.next[index].isDel==false&&nowNode.next[index].value==value){nowNode.next[index].isDel=true;return true;}//到下一个对应节点nowNode=nowNode.next[index];level++;			}	}}

测试

package datastructure.tree.hashtree;public class Main {public static void main(String[] args) {HashTree tree=new HashTree();System.out.println(tree.root);tree.insertNode(2);tree.insertNode(3);tree.insertNode(4);tree.insertNode(4);System.out.println(tree.root);System.out.println(tree.searchNode(3));tree.deleteNode(3);System.out.println(tree.root);System.out.println(tree.searchNode(3));System.out.println(tree.searchNode(2));System.out.println(tree.searchNode(4));}}