一、循序链表简介

1、循环链表的定义

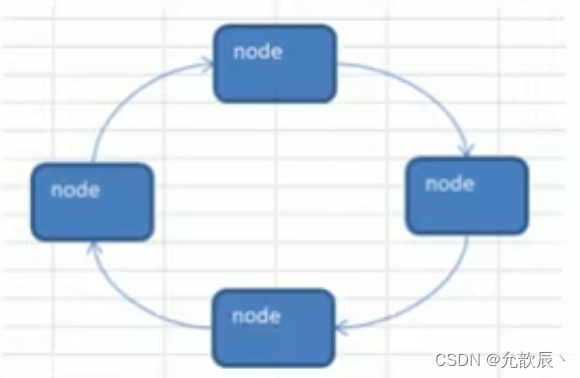
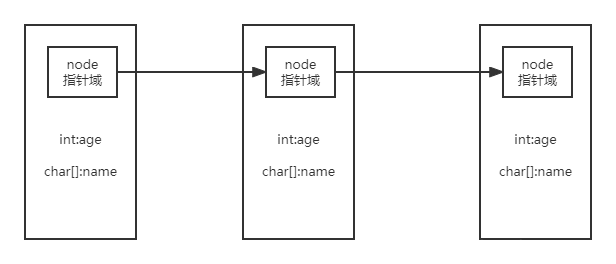
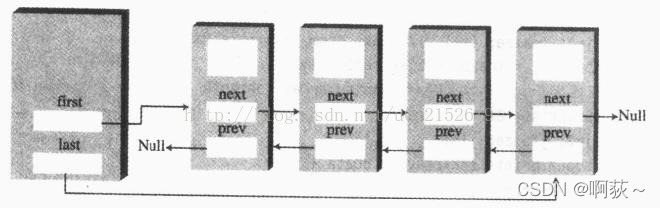
循环链表的任意元素都有一个前驱和一个后继，所有数据元素在关系上构成逻辑上的环。

循环链表是一种特殊的单链表，尾结点的指针指向首结点的地址。

循环链表的逻辑关系图如下：

 2、循环链表的设计实现

循环链表的设计实现要点：

A、通过模板定义CircleList，继承自LinkedList

B、定义连接链表首尾的内部函数

C、实现首元素的插入和删除操作

D、重写清空操作和遍历操作

3、循环链表的实现关键

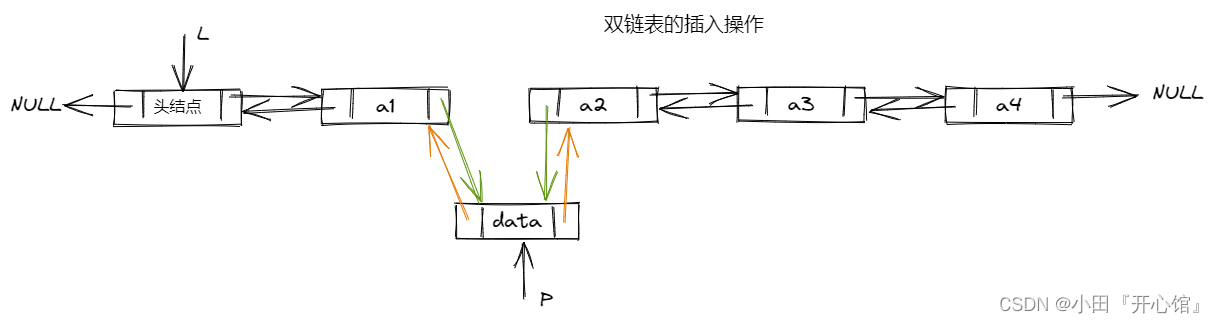
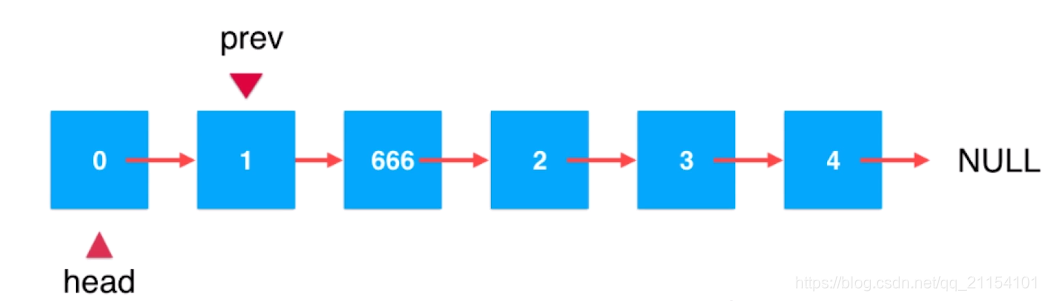
A、插入位置为0时，头结点和尾结点均指向新结点，新结点作为首结点插入链表。

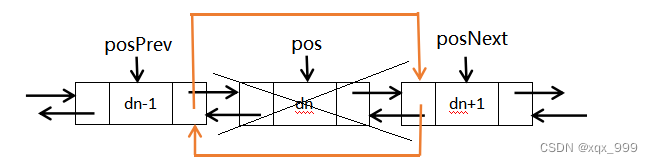
B、删除位置为0时，头结点和尾结点指向位置为1的结点，删除销毁首结点

二、循环链表的操作

1、尾结点获取

Node* last()
{return this->position(this->m_length - 1)->next;
}

2、首尾结点连接

void lastToFirst()
{last()->next = this->m_header.next;
}

3、循环链表的实现

  template <typename T>class CircleList:public LinkedList<T>{protected:typedef typename LinkedList<T>::Node Node;//尾结点Node* last(){return this->position(this->m_length - 1)->next;}//链接最后一个结点和首结点void lastToFirst(){last()->next = this->m_header.next;}int mod(int index)const{return (this->m_length == 0)?0:(index % this->m_length);}public:bool insert(int index, const T& value){bool ret = true;//计算插入结点的位置index = index % (this->m_length + 1);ret = LinkedList<T>::insert(index, value);//如果插入位置为0if(ret && (index == 0)){lastToFirst();//连接首尾结点}return ret;}bool insert(const T& value){return insert(this->m_length, value);}bool remove(int index){bool ret = true;index = mod(index);//删除结点为首结点if(index == 0){//首结点Node* toDel = this->m_header.next;if(toDel){//将头结点的下一个结点指向首结点的下一个结点this->m_header.next = toDel->next;this->m_length--;//链表长度减1//链表不为空if(this->m_length > 0){lastToFirst();//连接新的首结点与尾结点if(this->m_current == toDel){this->m_current = toDel->next;}}else{//链表为空，置空this->m_header.next = NULL;this->m_current = NULL;}//销毁要删除的结点this->destroy(toDel);}else{ret = false;}}else{//删除的结点不是首结点，按单链表处理ret = LinkedList<T>::remove(index);}return ret;}bool set(int index, const T& value){index = mod(index);return LinkedList<T>::set(index, value);}T get(int index)const{index = mod(index);return LinkedList<T>::get(index);}bool get(int index, T& value){index = mod(index);return LinkedList<T>::get(index, value);}int find(const T& value){int ret = -1;//首结点Node* current = this->m_header.next;//遍历链表查找数据元素for(int i = 0; i < this->length(); i++){if(current->value == value){ret = i;break;}//移动游标current = current->next;}return ret;}void clear(){//删除链表中结点至头结点while(this->m_length > 1){remove(1);}//删除首结点if(this->m_length == 1){Node* toDel = this->m_header.next;this->m_header.next = NULL;this->m_current = NULL;this->m_length = 0;this->destroy(toDel);}}bool move(int pos, int step){pos = mod(pos);return LinkedList<T>::move(pos, step);}bool end(){return (this->m_length == 0) || (this->m_current == NULL);}~CircleList(){clear();}};

四、约瑟夫环（Josephus）

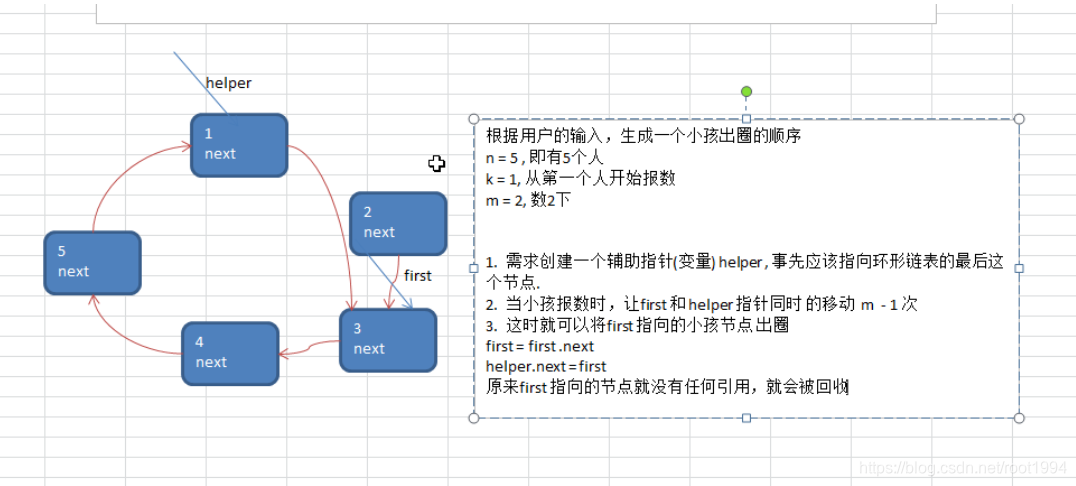
1、约瑟夫环简介

Josephu约瑟夫环问题为：设编号为1，2，… n的n个人围坐一圈，约定编号为k（1<=k<=n）的人从1开始报数，数到m 的那个人出列，它的下一位又从1开始报数，数到m的那个人又出列，依次类推，直到所有人出列为止，由此产生一个出队编号的序列。

2、循环链表解决约瑟夫环问题

//约瑟夫环
void jusephus(int n, int k, int m)
{//构建循环链表CircleList<int> cl;for(int i = 1; i <= n; i++){cl.insert(i);}//移动当前结点到位置k-1，设置步长为m-1cl.move(k-1, m-1);while(cl.length() > 0){cl.next();//移动到目标位置cout << cl.current() << endl;//删除目标位置结点cl.remove(cl.find(cl.current()));}
}

3、递归方法解决约瑟夫环问题

当编号为1开始时可以使用递归

假设n=10,m=3

1 2 3 4 5 6 7 8 9 10 m=3

第一次有人出列后：1 2 4 5 6 7 8 9 10

出环的序列：4 5 6 7 8 9 10 1 2

转换为：1 2 3 4 5 6 7 8 9

              +3: 4 5 6 7 8 9 10 11 12

             %10: 4 5 6 7 8 9 10 1 2

设f(n,m,i)为n个人的环，报数为m，第i个人出环的编号，则f(10,3,10)是我们要的结果

当i=1时，  f(n,m,i) = (n-1+m)%n

当i>1时，  f(n,m,i)= ( f(n-1,m,i-1)+m )%n

当编号为0开始时可以使用递归

假设n=10,m=3

0 1 2 3 4 5 6 7 8 9 m=3

第一次有人出列后：0 1 3 4 5 6 7 8 9

3 4 5 6 7 8 9 0 1

1 2 3 4 5 6 7 8 9

              +3: 4 5 6 7 8 9 10 11 12

             %10: 3 4 5 6 7 8 9 1 2

设f(n,m,i)为n个人的环，报数为m，第i个人出环的编号，则f(10,3,10)是我们要的结果

当i=1时，  f(n,m,i) = (n-1+m)%n

当i>1时，  f(n,m,i)= ( f(n-1,m,i-1)+m )%n

#include <stdio.h>
#include <stdlib.h>int Josephu_recursion(int n, int m, int i)
{if(1 == i)return (n-1 + m) % n;elsereturn (Josephu_recursion(n-1, m, i-1) + m) % n;
}int main(void)
{int i;for(i = 1; i <= 10; i ++)printf("第%2d次出环：%2d\n", i, Josephu_recursion(10, 3, i));
}

4、数组方法解决约瑟夫环问题

/************************************************ 约瑟夫环问题的数组解决* n:约瑟夫环的长度* k:起点* m:步长* *********************************************/
int JosephuArray(int n, int k, int m)
{//分配n+1个int空间int *a = (int *)malloc((n+1) * sizeof(int));int i, j;//下标从1开始赋值for(i = 1; i <= n; i++)a[i] = i;//从a[1]开始//依次出环for(i = n; i >= 1; i--){//计算每次出环的k值k = (k + m -1) % i;if(k == 0)k = i;printf("%2d\n", a[k]);//打印出出环的序号//将出环的位置后的元素前移for(j = k; j < i; j++)a[j] = a[j+1];}free(a);
}