ISCC客服冲冲冲

这里肯定是写一个脚本去自动化点击左边那个按钮，我本来想不会，百度一下发现还是很简单的一串js，果然还是要去学习脚本语言
console里添加

setInterval(function(){document.getElementById("按钮id").click();},1);
setInterval(function(){document.getElementById("left_button").click();},1);

https://www.jb51.net/article/132665.htm

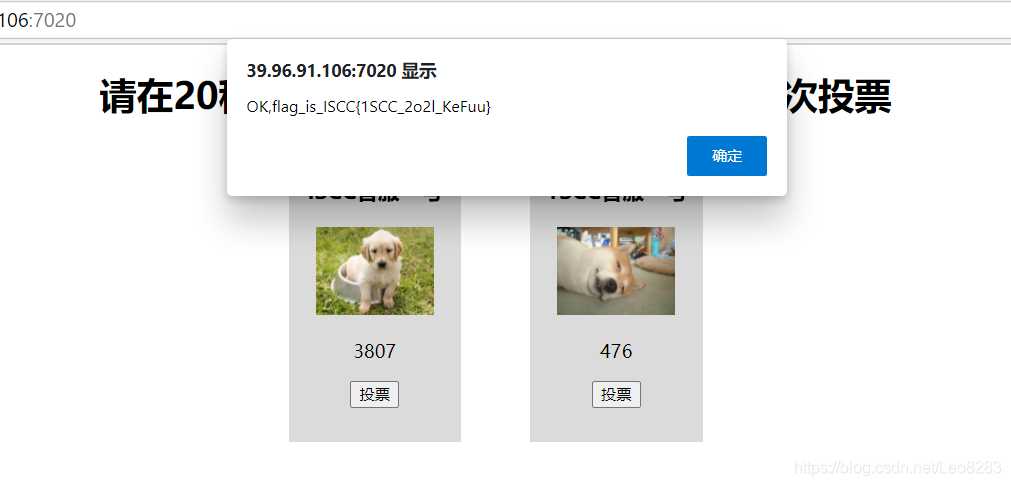
这是啥

源码里发现jsFuck编码
直接复制到console里运行
可以把jsFuck末尾的()去掉，可以看到源码

Web01

在这里插入代码片<?php
<p>code.txt</p>if (isset ($_GET['password'])) {if (preg_match ("/^[a-zA-Z0-9]+$/", $_GET['password']) === FALSE){echo '<p>You password must be alphanumeric</p>';}else if (strlen($_GET['password']) < 8 && $_GET['password'] > 9999999){    if (strpos ($_GET['password'], '*-*') !== FALSE){die('Flag: ' . $flag);}	else{echo('<p>*-* have not been found</p>');}}else{echo '<p>Invalid password</p>';}
}
?>

利用科学计数法，也利用了php弱类型比较
payload：password=9e9*-*
9成10的9次方

登录

不得不说，这题我昨天刚做过，看这个界面
这题原题[0CTF 2016]piapiapia
用的是反序列化变量逃逸