偶尔会用到关于矩阵元素的求和，总结一下常用的

目录

1、向量求和

2、矩阵求和

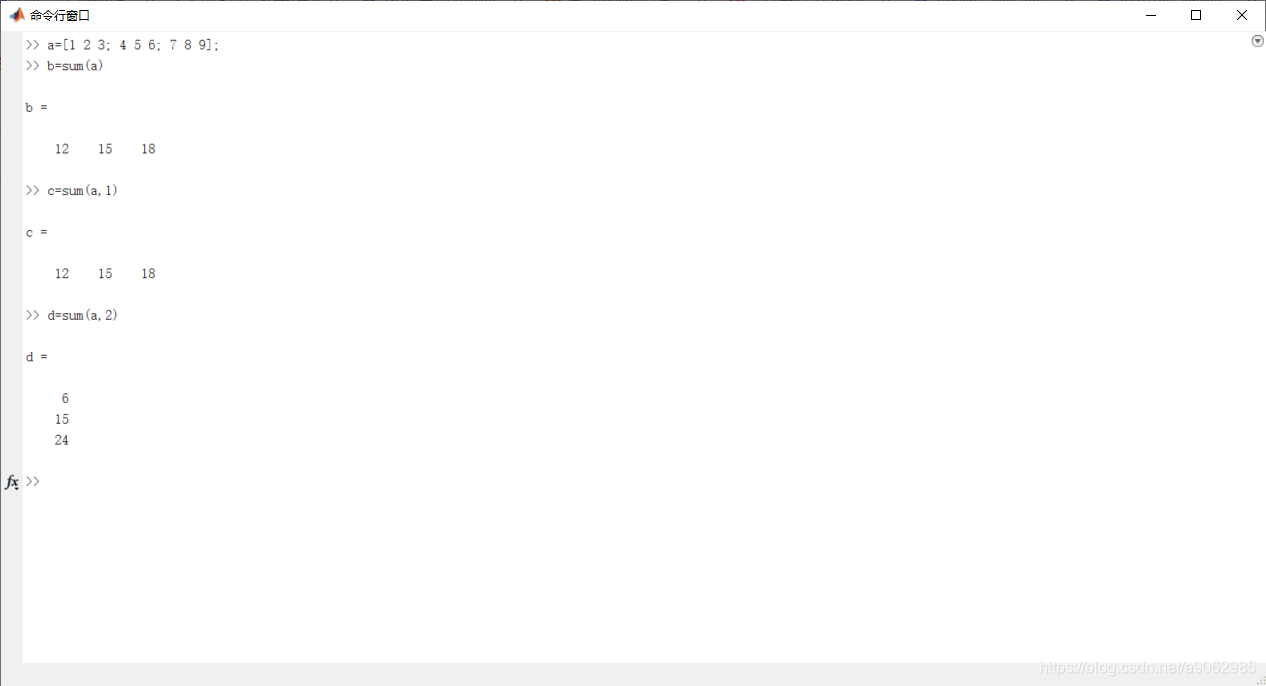
（1）默认按列求和，得到一个行向量 

（2）求每一行的和

3、sum和repmat一起使用

（1）矩阵A中每一行的平方和

（2）repmat的基本用法

（3）高斯核的计算

---

1、向量求和

直接调用sum即可，得到所有元素的和

a = [1 3 5 7];
s = sum(a); 

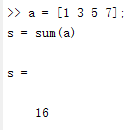
2、矩阵求和

调用格式：

s = sum(A,dim); % dim = 1，按列求和；dim = 2，按行求和

（1）默认按列求和，得到一个行向量 

（2）求每一行的和

b = [1 3 5 7;2 4 6 8]
s = sum(b,2)； % 得到一个列向量

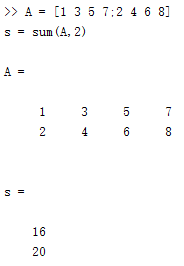
3、sum和repmat一起使用

结合repmat使用，可以节省一些for循环的运算，比如支持向量机中的核函数的表示（高斯核）

（1）矩阵A中每一行的平方和

A = [1 3 5 7;2 4 6 8];
s = sum(A.*A,2); % 对应元素点乘，再按行相加

（2）repmat的基本用法

% A可以是向量或矩阵

B = repmat(A,m,n); % 产生m行n列的A，并组成矩阵

（3）高斯核的计算

% A是m1行n列的矩阵；C是m行n列的矩阵KA = exp(-(repmat(sum(A.*A,2),1,m)+repmat(sum(C.*C,2)',m1,1)-2*A*C')/(p^2)); % K(A,C)

订正：图片最后的结果少了一个负号