前言
最近项目开发涉及商品SKU,商品SKU计算原理就是笛卡尔积,下面对相关内容做一下总结。
一、什么是SKU
SKU=Stock Keeping Unit(库存量单位),即库存进出计量的单位,可以是以件,盒,托盘等为单位。针对电商而言,一款商品SKU主要由商品规格组合,后面会举例子说明。
二、什么是笛卡尔积
笛卡尔乘积是指在数学中,两个集合X和Y的笛卡尓积(Cartesian product),又称直积,表示为X×Y,第一个对象是X的成员而第二个对象是Y的所有可能有序对的其中一个成员 。
假设集合A={a, b},集合B={0, 1, 2},则两个集合的笛卡尔积为{(a, 0), (a, 1), (a, 2), (b, 0), (b, 1), (b, 2)}。
这里针对商品举例说明,假设衣服由2个规格组成:颜色(黑色、白色)、尺寸(S、M、L),则根据SKU定义和笛卡尔积原理,生成SKU如下:
{('黑色', 'S'), ('黑色', 'M'), ('黑色', 'M'), ('白色', 'S'), ('白色', 'M'), ('白色', 'L')}三、代码实现
通过上面介绍,我们简单SKU和笛卡尔积,我们知道2个集合怎么生成SKU,但如果3个集合,怎么使用笛卡尔积实现SKU呢。这里我们可以采用分治的方案。就是先把两个集合生成SKU,作为一个集合,再和下一个集合进行笛卡尔积,这样就可以实现三个集合及以上问题。
1.第一方案
type GoodsSpec struct {Id int64 `json:"id"`Name string `json:"name"`
}func main() {// 颜色colorSpec := []GoodsSpec{{Id: 1,Name: "白色",},{Id: 2,Name: "黑色",},}// 尺寸sizeSpec := []GoodsSpec{{Id: 3,Name: "S",},{Id: 4,Name: "M",},{Id: 5,Name: "L",},}// 产地fieldSpec := []GoodsSpec{{Id: 9,Name: "杭州",},{Id: 10,Name: "北京",},}skus := GenerateSku(colorSpec, sizeSpec, fieldSpec)for _, sku := range skus {log.Printf("%+v", sku)}
}func GenerateSku(specs ...[]GoodsSpec) [][]GoodsSpec {skus := make([][]GoodsSpec, 0)for _, spec := range specs[0] {skus = append(skus, []GoodsSpec{spec})}for i := 0; i < len(specs)-1; i++ {skuTemp := make([][]GoodsSpec, 0)for _, sku := range skus {for _, spec := range specs[i+1] {temp := make([]GoodsSpec, 0)temp = append(temp, sku...)temp = append(temp, spec)skuTemp = append(skuTemp, temp)}}skus = skuTemp}return skus
}运行结果:
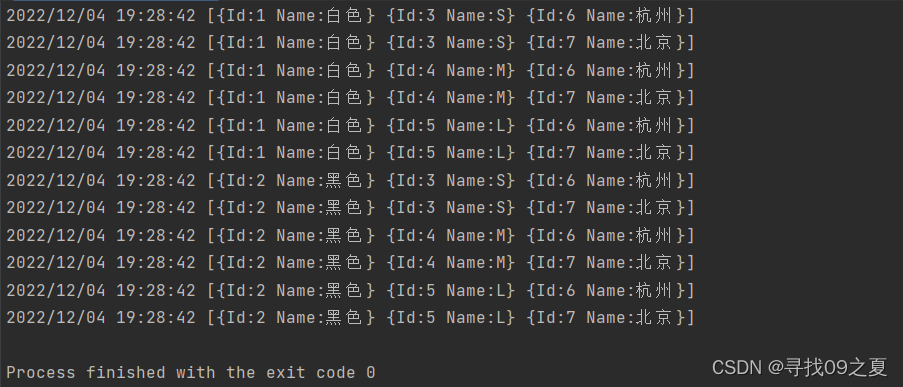
2.第二方案
type GoodsSpec struct {Id int64 `json:"id"`Name string `json:"name"`
}func main() {// 颜色colorSpec := []GoodsSpec{{Id: 1,Name: "白色",},{Id: 2,Name: "黑色",},}// 尺寸sizeSpec := []GoodsSpec{{Id: 3,Name: "S",},{Id: 4,Name: "M",},{Id: 5,Name: "L",},}// 产地fieldSpec := []GoodsSpec{{Id: 6,Name: "杭州",},{Id: 7,Name: "北京",},}sets := GenerateSku(colorSpec, sizeSpec, fieldSpec)for _, set := range sets {fmt.Printf("%+v\n", set)}
}func GenerateSku(specs ...[]GoodsSpec) [][]GoodsSpec {lens := func(i int) int {log.Printf("%+v", i)return len(specs[i])}var skus [][]GoodsSpecfor ix := make([]int, len(specs)); ix[0] < lens(0); nextIndex(ix, lens) {var r []GoodsSpecfor j, k := range ix {r = append(r, specs[j][k])}skus = append(skus, r)}return skus
}func nextIndex(ix []int, lens func(i int) int) {for j := len(ix) - 1; j >= 0; j-- {ix[j]++if j == 0 || ix[j] < lens(j) {return}ix[j] = 0}
}
运行结果:
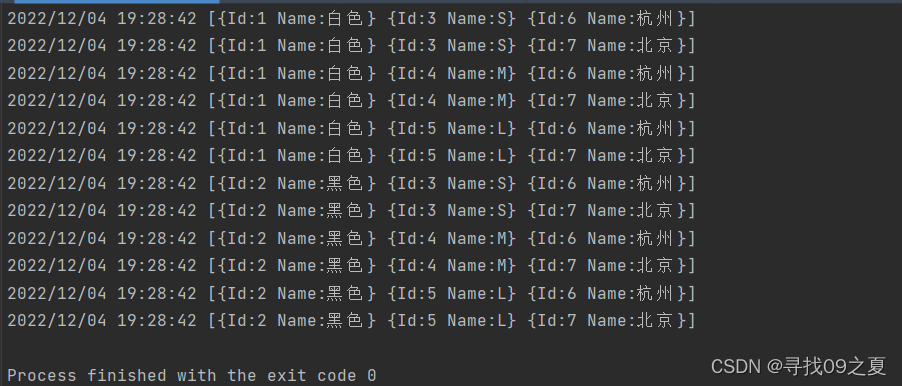
总结
1.先计算第一个集合和第二个集合的笛卡尔积,把结果保存为一个新集合。
2.然后再用新集合与下一个集合计算笛卡尔积,依此循环直到与最后一个集合计算笛卡尔积。