1. 什么是凸集、凸函数、凸学习问题?
凸集:若对集合C中任意两点u和v,连接他们的线段仍在集合C中,那么集合C是凸集。
公式表示为:αu+(1-α)v∈C α∈[0, 1]
凸函数:凸集上的函数是凸函数。凸函数的每一个局部极小值也是全局极小值( f(x) = 0.5x^2 )。
公式表示为:f(αu + (1-α)v) ≤ αf(u)+ (1-α)f(v)
2. L0、L1、L2正则化?
L0范数:计算向量中非0元素的个数。
L1范数:计算向量中各元素绝对值之和。
L2范数:计算向量中各元素平方和的开方。
L0范数和L1范数目的是使参数稀疏化。L1范数比L0范数容易优化求解。
L2范数是防止过拟合,提高模型的泛化性能。
3. 无监督学习方法有哪些?
强化学习、K-means 聚类、自编码、受限波尔兹曼机
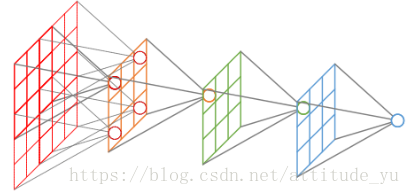
4. 空洞卷积(dilated convolution)的理解?
基于FCN的语义分割问题中,需保持输入图像与输出特征图的size相同。
若使用池化层,则降低了特征图size,需在高层阶段使用上采样,由于池化会损失信息,所以此方法会影响导致精度降低;
若使用较小的卷积核尺寸,虽可以实现输入输出特征图的size相同,但输出特征图的各个节点感受野小;
若使用较大的卷积核尺寸,由于需增加特征图通道数,此方法会导致计算量较大;
所以,引入空洞卷积(dilatedconvolution),在卷积后的特征图上进行0填充扩大特征图size,这样既因为有卷积核增大感受野,也因为0填充保持计算点不变。
5. 增大感受野的方法?
空洞卷积、池化操作、较大卷积核尺寸的卷积操作
6. 卷积层中感受野大小的计算?
卷积层的感受野大小与其之前层的卷积核尺寸和步长有关,与padding无关。基于从深层向浅层递归计算的方式。
计算公式为:Fj-1 = Kj + (Fj - 1)*Sj(最后一层特征图的感受野大小是其计算卷积核大小)
7. 梯度下降法和牛顿法的优缺点?
优点:梯度下降法:可用于数据量较大的情况;
牛顿法:收敛速度更快;
缺点:梯度下降法:每一步可能不是向着最优解的方向;
牛顿法:每次迭代的时间长;需要计算一阶和二阶导数;
8. 解决训练样本类别不平衡问题?
现象:训练样本中,正负样本数量的比例较大。
1. 过采样。增加正例样本数量,使得正负样本数量接近,然后再进行学习。
2. 欠采样。去除反例样本数量,使得正负样本数量接近,然后再进行学习。
3. 设置阈值。基于原始数据集学习,当使用已训练好的分类器进行预测时,将正负样本数量的比例作为阈值嵌入到决策过程中。
9. 各个激活函数的优缺点?
Sigmoid激活函数 缺点:
1. 不是关于原点对称;
2. 需要计算exp
Tanh 激活函数 优点:
1. 关于原点对称
2. 比sigmoid梯度更新更快
ReLU激活函数 优点:
1. 神经元输出为正时,没有饱和区
2. 计算复杂度低,效率高
3. 在实际应用中,比sigmoid、tanh更新更快
4. 相比于sigmoid更加符合生物特性
ReLU激活函数 缺点:
1. 神经元输出为负时,进入了饱和区
2. 神经元的输出在非0中心
3. 使得数据存在Activ