作者 | Tomer Amit

译者 | 弯月，编辑 | 屠敏

出品 | CSDN（ID：CSDNnews）

在本文中，我将分享有关深度学习的25个问题，希望能够帮助你为面试做好准备。

1.为什么必须在神经网络中引入非线性？

答：否则，我们将获得一个由多个线性函数组成的线性函数，那么就成了线性模型。线性模型的参数数量非常少，因此建模的复杂性也会非常有限。

2.说明解决神经网络中梯度消失问题的两种方法。

答：

• 使用ReLU激活函数代替S激活函数。

• 使用Xavier初始化。

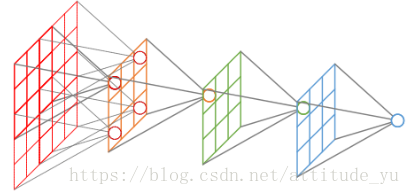
3.在图像分类任务中，相较于使用密集神经网络（Dense Neural Network，DNN），使用卷积神经网络（Convolutional Neural Network，CNN）有哪些优势？

答：虽然两种模型都可以捕获彼此靠近的像素之间的关系，但CNN具有以下属性：

• 它是平移不变的：对于过滤器而言，像素的确切位置是无关的。

• 更不容易发生过度拟合：一般而言CNN中的参数比DNN要少很多。

• 方便我们更好地理解模型：我们可以查看过滤器的权重，并可视化神经网络的学习成果。

• 分层性质：通过使用较简单的模式描述复杂的模式来学习模式。

4. 说明在图像分类任务中可视化CNN特征的两种方法。

答：

• 输入遮挡：遮挡输入图像的一部分，看看哪部分对分类的影响最大。 例如，针对某个训练好的图像分类模型，将下列图像作为输入。如果我们看到第三幅图像被分类为狗狗的概率为98%，而第二幅图像的准确率仅为65%，则说明眼睛对于对分类的影响更大。

• 激活最大化：创建一个人造的输入图像，以最大化目标响应（梯度上升）。

5. 在优化学习速率时，分别尝试学习速率：0.1、0.2，…，0.5是好办法吗？

答：这种方法并不好，建议使用对数比例来优化学习速率。

6. 假设一个神经网络拥有3层的结构和ReLU激活函数。如果我们用同一个值初始化所有权重，结果会怎样？如果我们只有1层（即线性/逻辑回归）会怎样？

答：如果所有权重的初始值都相同，则无法破坏对称性。也就是说，所有梯度都会更新成同一个值，而且神经网络将无法学习。但是，如果神经网络只有1层的话，成本函数是凸形的（线性/ S型），因此权重始终会收敛到最佳点，无论初始值是什么（收敛可能会较慢）。

7.解释Adam优化器的概念。

答：Adam结合了两个想法来改善收敛性：每个参数更新可加快收敛速度；动量可避免卡在鞍点上。

8.比较批处理，小批处理和随机梯度下降。

答：批处理是指在估计数据时获取整个数据；小批处理是通过对几个数据点进行采样来进行小批量处理；而随机梯度下降是指在每个时期更新一个数据点的梯度。我们需要权衡梯度计算的准确度与保存在内存中的批量大小。此外，通过在每个epoch添加随机噪声，我们可以通过小批处理（而非整个批处理）实现正规化效果。

9.什么是数据扩充？举个例子。

答：数据扩充是一种技术，通过操作原始数据来增加输入数据。例如，对于图像，我们可以执行以下操作：旋转图像、翻转图像、添加高斯模糊等。

10. 解释GAN的概念。

答：GAN（Generative Adversarial Network）即生成对抗网络，通常由两个神经网络D和G组成，其中D指的是判别器（Discriminator），而G指生成网络（Generative Network）。这种模型的目标是创建数据，例如创建与真实图像并无二样的图像。假设我们想要创建一只猫的对抗示例。神经网络G负责生成图像，而神经网络D则负责判断图像是否是猫。G的目标是“愚弄”D——将G的输出始终分类为猫。

11.使用Batchnorm有什么优势？

答：Batchnorm能够加快训练过程，而且（一些噪音的副产品）还具有调节作用。

12.什么是多任务学习？应该在什么时候使用？

答：当我们使用少量数据处理多个任务时，多任务处理将很有用，而且我们还可以使用在其他任务的大型数据集上训练好的模型。通过“硬”方式（即相同的参数）或“软”方式（即对成本函数进行正则化/惩罚）共享模型的参数。

13.什么是端到端学习？列举一些优点。

答：端到端学习通常是一个模型，该模型能够获取原始数据并直接输出所需的结果，而无需任何中间任务或功能工程。其优点包括：无需手工构建功能，而且通常可以降低偏差。

14.如果在最后一层中，我们先使用ReLU激活函数，然后再使用Sigmoid函数，会怎样？

答：由于ReLU始终会输出非负结果，因此该神经网络会将所有输入预测成同一个类别。

15.如何解决梯度爆炸的问题？

答：解决梯度爆炸问题的一个最简单的方法就是梯度修剪，即当梯度的绝对值大于M（M是一个很大的数字）时，设梯度为±M。

16.使用批量梯度下降法时，是否有必要打乱训练数据？

答：没有必要。因为每个epoch的梯度计算都会使用整个训练数据，所以打乱顺序也没有任何影响。

17.当使用小批量梯度下降时，为什么打乱数据很重要？ 

答：如果不打乱数据的顺序，那么假设我们训练一个神经网络分类器，且有两个类别：A和B，那么各个epoch中的所有小批量都会完全相同，这会导致收敛速度变慢，甚至导致神经网络对数据的顺序产生倾向性。

18.列举迁移学习的超参数。

答：保留多少层、添加多少层、冻结多少层。

19. 测试集上是否需要使用dropout？

答：不可以使用！dropout只能用于训练集。dropout是训练过程中应用的一种正则化技术。

20.说明为什么神经网络中的dropout可以作为正则化。

答：关于dropout的工作原理有几种解释。我们可以将其视为模型平均的一种形式：我们可以在每一步中“去掉”模型的一部分并取平均值。另外，它还会增加噪音，自然会产生调节的效果。最后，它还可以稀释权重，从根本上阻止神经网络中神经元的共适应。

21. 举个适合多对一RNN架构的例子。

答：例如：情绪分析，语音中的性别识别等。

22.我们什么时候不能使用BiLSTM？说明在使用BiLSTM我们必须做的假设。

答：在所有双向模型中，我们都可以假设在给定的“时间”内访问序列的下一个元素。文本数据（例如情感分析、翻译等）就是这种情况，而时间序列数据则不属于这种情况。

23. 判断对错：将L2正则化添加到RNN有助于解决梯度消失的问题。

答：错误！添加L2正则化会将权重缩小为零，在某些情况下这实际上会让梯度消失的问题更严重。

24. 假设训练错误/成本很高，而且验证成本/错误几乎与之相等。这是什么意思？我们应该做些什么？

答：这表明欠拟合。我们可以添加更多参数，增加模型的复杂性或减少正则化。

25. 说明为何L2正则化可以解释为一种权重衰减。

答：假设我们的成本函数为C(w)，我们再加上一个c|w|2。使用梯度下降时，迭代如下：

w = w -grad(C)(w) — 2cw = (1–2c)w — grad(C)(w)

在该等式中，权重乘以因子<1

原文链接：

https://towardsdatascience.com/50-deep-learning-interview-questions-part-1-2-8bbc8a00ec61

【End】

推荐阅读半小时训练亿级规模知识图谱，亚马逊AI开源知识图谱嵌入表示框架DGL-KE
首次揭秘！大麦如何应对超大规模高性能选座抢票？
AI 四巨头 Google、DeepMind、Microsoft、Uber 深度学习框架大比拼马化腾、马云并列成为中国首富；百度回应“将上线电商直播”；.NET 5 Preview 2 发布 | 极客头条程序员职场背锅甩锅指南警惕！新骗术出现：这些虚假二维码生成器已成功盗取 4.6 万美元！“出道” 5 年采用率达 78%，Kubernetes 的成功秘诀是什么？

• 

  你点的每个“在看”，我都认真当成了AI