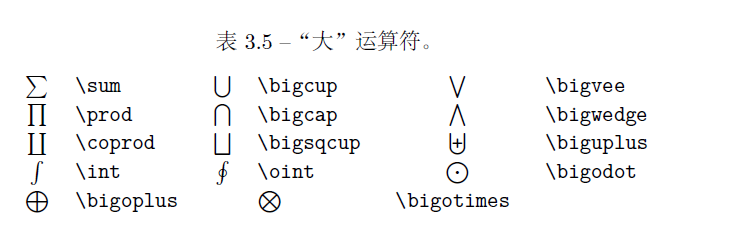
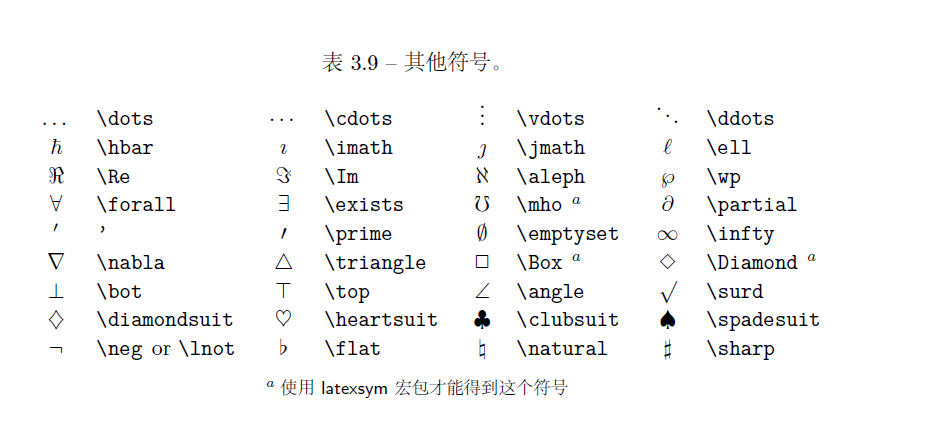
果然是自己搞一个查起来会方便一些,最近天天写数学题解,全是公式 ~
希腊字母:
| 字母名称 | 国际音标 | 大写字母 | 小写字母 | 字母名称 | 国际音标 | 大写字母 | 小写字母 |
|---|---|---|---|---|---|---|---|
| alpha | /'ælfə/ | Α | α | nu | /nju:/ | Ν | ν |
| beta | /'bi:tə/或 /'beɪtə/ | Β | β | xi | 希腊 /ksi/;英美 /ˈzaɪ/ 或 /ˈksaɪ/ | Ξ | ξ |
| gamma | /'gæmə/ | Γ | γ | omicron | /əuˈmaikrən/或 /ˈɑmɪˌkrɑn/ | Ο | ο |
| delta | /'deltə/ | Δ | δ | pi | /paɪ/ | Π | π |
| epsilon | /'epsɪlɒn/ | Ε | ε | rho | /rəʊ/ | Ρ | ρ |
| zeta | /'zi:tə/ | Ζ | ζ | sigma | /'sɪɡmə/ | Σ | σ, ς |
| eta | /'i:tə/ | Η | η | tau | /tɔ:/ 或 /taʊ/ | Τ | τ |
| theta | /'θi:tə/ | Θ | θ | upsilon | /ˈipsilon/或 /ˈʌpsɨlɒn/ | Υ | υ |
| iota | /aɪ’əʊtə/ | Ι | ι | phi | /faɪ/ | Φ | φ |
| kappa | /'kæpə/ | Κ | κ | chi | /kaɪ/ | Χ | χ |
| lambda | /'læmdə/ | Λ | λ | psi | /psaɪ/ | Ψ | ψ |
| mu | /mju:/ | Μ | μ | omega | /'əʊmɪɡə/或 /oʊ’meɡə/ | Ω | ω |
摘自:《一份不太简短的LATEX2介绍》或112分钟学会LATEX2 原版作者:Tobias Oetiker
等式对齐
t e x t = 12345 = 67890 = 13579 \begin{aligned} text & = 12345 & \\ &= 67890 & \\ &= 13579\end{aligned} text=12345=67890=13579
源码:
$$\begin{aligned} text & = 12345 & \\ &= 67890 & \\ &= 13579\end{aligned}$$
例:
φ ( n ) = n × ∏ i = 1 s p i − 1 p i = p 1 × n ′ × ∏ i = 1 s p i − 1 p i = p 1 × φ ( n ′ ) \begin{aligned} \varphi(n) & = n \times \prod_{i = 1}^s{\frac{p_i - 1}{p_i}} & \\ &= p_1 \times n' \times \prod_{i = 1}^s{\frac{p_i - 1}{p_i}} & \\ &= p_1 \times \varphi(n') \end{aligned} φ(n)=n×i=1∏spipi−1=p1×n′×i=1∏spipi−1=p1×φ(n′)
源码:
$$\begin{aligned} \varphi(n) & = n \times \prod_{i = 1}^s{\frac{p_i - 1}{p_i}} & \\ &= p_1 \times n' \times \prod_{i = 1}^s{\frac{p_i - 1}{p_i}} & \\ &= p_1 \times \varphi(n') \end{aligned}$$
大括号
方法一:$$ f(x)=\left\{
\begin{aligned}
x & = & \cos(t) \\
y & = & \sin(t) \\
z & = & \frac xy
\end{aligned}
\right.
$$方法二:
$$ F^{HLLC}=\left\{
\begin{array}{rcl}
F_L & & {0 < S_L}\\
F^*_L & & {S_L \leq 0 < S_M}\\
F^*_R & & {S_M \leq 0 < S_R}\\
F_R & & {S_R \leq 0}
\end{array} \right. $$方法三:
$$f(x)=
\begin{cases}
0& \text{x=0}\\
1& \text{x!=0}
\end{cases}$$
方法一:
f ( x ) = { x = cos ( t ) y = sin ( t ) z = x y f(x)=\left\{ \begin{aligned} x & = & \cos(t) \\ y & = & \sin(t) \\ z & = & \frac xy \end{aligned} \right. f(x)=⎩⎪⎪⎨⎪⎪⎧xyz===cos(t)sin(t)yx
方法二:
F H L L C = { F L 0 < S L F L ∗ S L ≤ 0 < S M F R ∗ S M ≤ 0 < S R F R S R ≤ 0 F^{HLLC}=\left\{ \begin{array}{rcl} F_L & & {0 < S_L}\\ F^*_L & & {S_L \leq 0 < S_M}\\ F^*_R & & {S_M \leq 0 < S_R}\\ F_R & & {S_R \leq 0} \end{array} \right. FHLLC=⎩⎪⎪⎨⎪⎪⎧FLFL∗FR∗FR0<SLSL≤0<SMSM≤0<SRSR≤0
方法三:
f ( x ) = { 0 x=0 1 x!=0 f(x)= \begin{cases} 0& \text{x=0}\\ 1& \text{x!=0} \end{cases} f(x)={01x=0x!=0
矩阵
$$
\begin{gathered}
\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}
\quad
\begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix}
\quad
\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}
\quad
\begin{Bmatrix} 1 & 0 \\ 0 & -1 \end{Bmatrix}
\quad
\begin{vmatrix} a & b \\ c & d \end{vmatrix}
\quad
\begin{Vmatrix} i & 0 \\ 0 & -i \end{Vmatrix}
\end{gathered}
$$
0 1 1 0 ( 0 − i i 0 ) [ 0 − 1 1 0 ] { 1 0 0 − 1 } ∣ a b c d ∣ ∥ i 0 0 − i ∥ \begin{gathered} \begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix} \quad \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix} \quad \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \quad \begin{Bmatrix} 1 & 0 \\ 0 & -1 \end{Bmatrix} \quad \begin{vmatrix} a & b \\ c & d \end{vmatrix} \quad \begin{Vmatrix} i & 0 \\ 0 & -i \end{Vmatrix} \end{gathered} 0110(0i−i0)[01−10]{100−1}∣∣∣∣acbd∣∣∣∣∥∥∥∥i00−i∥∥∥∥
A= \overbrace{\left[\begin{array}{ccc}1 & 2 & 3 \\1 & 2 & 3 \\1 & 2 & 3 \\\end{array}\right]}^{2^{3}}
A = [ 1 2 3 1 2 3 1 2 3 ] ⏞ 2 3 A= \overbrace{\left[ \begin{array}{ccc} 1 & 2 & 3 \\ 1 & 2 & 3 \\ 1 & 2 & 3 \\ \end{array} \right]}^{2^{3}} A=⎣⎡111222333⎦⎤ 23
A = \left.\left[\begin{array}{ccc}1 & 2 & 3 \\1 & 2 & 3 \\1 & 2 & 3 \\\end{array}\right]\right\}2^{3}
A = [ 1 2 3 1 2 3 1 2 3 ] } 2 3 A = \left.\left[ \begin{array}{ccc} 1 & 2 & 3 \\ 1 & 2 & 3 \\ 1 & 2 & 3 \\ \end{array} \right]\right\}2^{3} A=⎣⎡111222333⎦⎤⎭⎬⎫23
部分内容摘自:《一份不太简短的LATEX2介绍》或112分钟学会LATEX2 原版作者:Tobias Oetiker