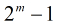给出2个大整数A,B,计算A+B的结果。
Input
第1行:大数A 第2行:大数B (A,B的长度 <= 10000 需注意:A B有可能为负数)
Output
输出A + B
Input示例
68932147586 468711654886
Output示例
537643802472
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <string>
#include <string.h>
#include <cmath>
#include <vector>
using namespace std ;
struct BigInteger
{
static const int BASE = 10 ;
static const int WIDTH = 1 ;
vector < int > s ;
bool flag ;
BigInteger ( long long num = 0 ) { * this = num ; } // 构造函数
BigInteger operator = ( long long num )
{ // 赋值运算符
s . clear ( ) ;
if ( num < 0 )
{
flag = 0 ;
num = - num ;
}
else
flag = 1 ;
do
{
s . push_back ( num % BASE ) ;
num / = BASE ;
} while ( num > 0 ) ;
return * this ;
}
BigInteger operator = ( const string & str )
{ // 赋值运算符
s . clear ( ) ;
if ( str [ 0 ] == '-' )
flag = 0 ;
else
flag = 1 ;
string strr = str ;
if ( flag == 0 )
strr . erase ( 0 , 1 ) ;
int x , len = ( strr . length ( ) - 1 ) / WIDTH + 1 ;
int i = 0 ;
for ( ; i < len ; i ++ )
{
int end = strr . length ( ) - i * WIDTH ;
int start = max ( 0 , end - WIDTH ) ;
sscanf ( strr . substr ( start , end - start ) . c_str ( ) , "%d" , & x ) ;
s . push_back ( x ) ;
}
return * this ;
}
BigInteger operator + ( const BigInteger & b ) const
{
BigInteger c , d ;
if ( b . flag == 0 )
{
BigInteger B = b ;
B . flag = 1 ;
if ( flag == 0 )
{
d = * this ;
d . flag = 1 ;
c = d + B ;
c . flag = 0 ;
return c ;
}
return * this - B ;
}
if ( flag == 0 )
{
c = * this ;
c . flag = 1 ;
return b - c ;
}
c . s . clear ( ) ;
for ( int i = 0 , g = 0 ;; i ++ )
{
if ( g == 0 && i >= s . size ( ) && i >= b . s . size ( ))
break ;
int x = g ;
if ( i < s . size ( ))
x += s [ i ] ;
if ( i < b . s . size ( ))
x += b . s [ i ] ;
c . s . push_back ( x % BASE ) ;
g = x / BASE ;
}
return c ;
}
BigInteger operator * ( const BigInteger & b ) const
{
BigInteger c , t ;
if ( b . flag == flag )
c . flag = 1 ;
else
c . flag = 0 ;
c = 0 ;
for ( int i = 0 ; i < s . size ( ) ; i ++ )
{
t . s . clear ( ) ;
long long x , g ;
int j ;
j = i ;
while ( j -- )
t . s . push_back ( 0 ) ;
for ( j = g = 0 ;; j ++ )
{
if ( j >= b . s . size ( ) && g == 0 )
break ;
x = g ;
if ( j < b . s . size ( ))
x += s [ i ] * b . s [ j ] ;
t . s . push_back ( x % BASE ) ;
g = x / BASE ;
}
c += t ;
}
return c ;
}
BigInteger operator * ( const int & b ) const
{
BigInteger c = b ;
return c * ( * this ) ;
}
BigInteger operator * ( const long long int & b ) const
{
BigInteger c = b ;
return c * ( * this ) ;
}
BigInteger operator^ ( int b ) const
{
BigInteger ans = 1 , base = * this ;
while ( b )
{
if ( b & 1 )
{
ans = base * ans ;
}
base = base * base ;
b >>= 1 ;
}
return ans ;
}
BigInteger operator += ( const BigInteger & b ) const
{
return * this + b ;
}
bool operator < ( const BigInteger & b ) const
{
if ( b . flag == 0 && b . flag != flag )
return false ;
if ( s . size ( ) != b . s . size ( ))
return s . size ( ) < b . s . size ( ) ;
for ( int i = s . size ( ) - 1 ; i >= 0 ; i -- )
if ( s [ i ] != b . s [ i ])
return s [ i ] < b . s [ i ] ;
return false ;
}
bool operator > ( const BigInteger & b ) const { return b < * this ; }
bool operator <= ( const BigInteger & b ) const { return ! ( b < * this ) ; }
bool operator >= ( const BigInteger & b ) const { return ! ( * this < b ) ; }
bool operator != ( const BigInteger & b ) const { return b < * this || * this < b ; }
bool operator == ( const BigInteger & b ) const { return ! ( b < * this ) && ! ( * this < b ) ; }
BigInteger operator - ( const BigInteger & b ) const
{
if ( b . flag == 0 )
{
BigInteger B = b ;
B . flag = 1 ;
return * this + B ;
}
BigInteger A , B ;
A = * this ;
B = b ;
A . flag = 1 ;
B . flag = 1 ;
BigInteger c ;
if ( A < B )
{
swap ( A , B ) ; c . flag = 0 ;
}
c . s . clear ( ) ;
int i , g , x ;
i = g = 0 ;
while ( 1 ) //for (int i = 0, g = 0;; i++)
{
if ( i >= A . s . size ( ) && i >= B . s . size ( ))
break ;
x = A . s [ i ] ;
x -= g ;
g = 0 ;
if ( i < B . s . size ( ))
x -= B . s [ i ] ;
if ( x < 0 )
{
x += 10 ;
g = 1 ;
}
c . s . push_back ( x ) ;
i ++ ;
}
if ( c . s . back ( ) == 0 )
{
vector < int > :: iterator it = c . s . end ( ) ;
for ( it -- ; it != c . s . begin ( ) ; it -- )
{
if ( * it != 0 )
break ;
}
it ++ ;
c . s . erase ( it , c . s . end ( )) ;
}
if ( c . s . empty ( ))
c . s . push_back ( 0 ) ;
return c ;
}
BigInteger operator - ( const int & b ) const
{
BigInteger c = b ;
return * this - c ;
}
BigInteger operator - ( const long long int & b ) const
{
BigInteger c = b ;
return * this - c ;
}
BigInteger operator -= ( const BigInteger & b ) const { return * this - b ; }
BigInteger operator ! ( void ) const //阶乘
{
BigInteger ans = 1 ;
for ( BigInteger i = 1 ; i <= * this ; i += 1 )
{
ans = i * ans ;
}
return ans ;
}
BigInteger operator/ ( const BigInteger & b ) const
{
//A/B
BigInteger A , B , c , ans ;
if ( b . flag == flag )
ans . flag = 1 ;
else
ans . flag = 0 ;
if ( b > * this )
return 0 ;
if ( b == * this )
return 1 ;
c . s . clear ( ) ;
ans . s . clear ( ) ;
A = * this ;
B = b ;
A . flag = B . flag = c . flag = 1 ;
int zero = ( A . s . size ( ) - b . s . size ( )) ;
B . s . insert ( B . s . begin ( ) , zero , 0 ) ;
while ( ! B . s . empty ( ) && B >= b )
{
int x = 0 ;
while ( A >= B )
{
A = A - B ;
x ++ ;
}
c . s . push_back ( x ) ;
B . s . erase ( B . s . begin ( )) ;
}
if ( ! c . s . empty ( ))
for ( vector < int > :: reverse_iterator it = c . s . rbegin ( ) ; it != c . s . rend ( ) ; it ++ )
{
ans . s . push_back ( * it ) ;
}
else
ans . s . push_back ( 0 ) ;
if ( ans . s . empty ( ))
ans . s . push_back ( 0 ) ;
if ( ans . s . back ( ) == 0 )
{
vector < int > :: iterator it = ans . s . end ( ) ;
for ( it -- ; it != ans . s . begin ( ) ; it -- )
{
if ( * it != 0 )
break ;
}
it ++ ;
ans . s . erase ( it , ans . s . end ( )) ;
}
return ans ;
}
} ;
ostream & operator << ( ostream & out , const BigInteger & x )
{
if ( x . flag == 0 )
out << '-' ;
out << x . s . back ( ) ;
for ( int i = x . s . size ( ) - 2 ; i >= 0 ; i -- )
{
char buf [ 20 ] ;
sprintf ( buf , "%d" , x . s [ i ]) ;
for ( int j = 0 ; j < strlen ( buf ) ; j ++ )
out << buf [ j ] ;
}
return out ;
}
istream & operator >> ( istream & in , BigInteger & x )
{
string s ;
if ( ! ( in >> s ))
return in ;
x = s ;
return in ;
}
int main ( )
{
BigInteger a , b ;
cin >> a >> b ;
cout << a + b << endl ;
}