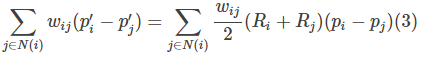论文As-Rigid-As-Possible Surface Modeling 发表于SGP 2007,是变形领域的经典论文,目前引用已经超过1000次。网格变形要求产生视觉合理并且大致满足物理规律的变形效果,而模型细节的保持很大程度地满足了这种需求。刚性作为一个重要的属性在保细节方面具有明显的优势,从某种意义上讲,保持模型的刚性很大程度地促进了模型表面细节的保持。
先来看看文中的变形效果:

本文主要讲一下论文中的旋转矩阵 R i R_i Ri的求解方法。
一、算法简介
如下图所示,ARAP变形算法首先定义网格顶点与1-邻域的边构成刚性变形单元,所有点的变形单元重叠地覆盖网格表面。

变形过程中假设变形单元仅仅发生旋转变换,形式化的表示如公式(1)所示,变形单元的刚性变换使得网格顶点相对于1-邻域顶点的位置保持不变,从而有效地保持了模型局部的细节。
p i ′ − p j ′ = R i ( p i − p j ) , ∀ j ∈ N ( i ) (1) p'_i-p'_j= R_i(p_i-p_j), \forall j \in N(i)\tag1 pi′−pj′=Ri(pi−pj),∀j∈N(i)(1)
其中, R i R_i Ri 是该变形单元对应的旋转矩阵, p i , p j p_i,p_j pi,pj 和 p i ′ , p j ′ p'_i,p'_j pi′,pj′ 是变形前后的网格顶点,这里点的表示是列向量。
每个变形单元的能量函数定义如下所示,通过最小化该能量函数实现模型的尽可能刚性变形:
E ( C i , C i ′ ) = ∑ j ∈ N ( i ) w i j ∣ ∣ ( p i ′ − p j ′ ) − R i ( p i − p j ) ∣ ∣ 2 (2) E(C_i,C_i' )= \sum_{j\in N(i)} w_{ij} \left| \left|(p'_i-p'_j) - R_i(p_i-p_j)\right|\right|^2 \tag2 E(Ci,Ci′)=j∈N(i)∑wij∣ ∣∣ ∣(pi′−pj′)−Ri(pi−pj)∣ ∣∣ ∣2(2)
ARAP变形算法总的能量函数定义为:
E = ∑ i = 1 n ∑ j ∈ N ( i ) w i j ∣ ∣ ( p i ′ − p j ′ ) − R i ( p i − p j ) ∣ ∣ 2 (3) E= \sum^n_{i=1}\sum_{j\in N(i)} w_{ij} \left| \left|(p'_i-p'_j) - R_i(p_i-p_j)\right|\right|^2 \tag3 E=i=1∑nj∈N(i)∑wij∣ ∣∣ ∣(pi′−pj′)−Ri(pi−pj)∣ ∣∣ ∣2(3)
其中, C i C_i Ci和 C i ′ C_i' Ci′分别表示变形前后模型顶点 p i p_i pi 和 p i ′ p'_i pi′ 对应的变形单元, N ( i ) N(i) N(i) 表示 p i p_i pi 的1-邻域点的索引,而 p j p_j pj 和 p j ′ p'_j pj′ 分别表示 p i p_i pi 和 p i ′ p'_i pi′ 的1-邻域顶点, R i R_i Ri表示 C i C_i Ci到 C i ′ C_i' Ci′的最优旋转矩阵, w i j w_{ij} wij是边 e i j = ( p i , p j ) e_{ij}=(p_i, p_j) eij=(pi,pj)的权重, 定义如下所示。其中, α i j \alpha_{ij} αij 和 β i j \beta_{ij} βij 如上图所示。
w i , j = 1 2 ( c o t α i j + c o t β i j ) (4) w_{i,j} = \frac{1}{2}(cot\alpha_{ij} + cot \beta_{ij})\tag4 wi,j=21(cotαij+cotβij)(4)
对于公式(3)所示的二次能量函数最小化中的每个变形单元,共有两个未知数:旋转矩阵 R R R 和变形后的点坐标 P ′ P' P′(公式(2)中的 p i ′ p'_i pi′ 和 p j ′ p'_j pj′). 论文采用迭代的方式进行优化求解:
- 1)固定 P ′ P' P′ 求解使得(3)最小的每个变形单元的最优旋转矩阵 R i R_i Ri。
- 2)在旋转矩阵 R i R_i Ri已知的情况下,求解使得(3)最小的变形后的顶点坐标 P ′ P' P′。
- 3)返回1),直到能量误差小于用户指定的阈值为止。
接下来,重点讲一下如何求解 R R R 和 P ′ P' P′.
二、已知 P ′ P' P′求解旋转矩阵 R R R
针对每个变形单元单独求解,令 e i j ′ = p i ′ − p j ′ , e i j = p i − p j e'_{ij} = p'_i-p'_j, e_{ij} = p_i-p_j eij′=pi′−pj′,eij=pi−pj, 公式(2)可以改写为:
E ( C i , C i ′ ) = ∑ j ∈ N ( i ) w i j ( e i j ′ − R i e i j ) 2 = ∑ j ∈ N ( i ) w i j ( e i j ′ T e i j ′ − e i j ′ T R i e i j + e i j T R i T R i e i j ) (5) E(C_i,C_i' )=\sum_{j\in N(i)}w_{ij}(e'_{ij}-R_ie_{ij})^2 =\sum_{j\in N(i)}w_{ij}(e'^T_{ij}e'_{ij}-e'^T_{ij}R_ie_{ij}+e^T_{ij}R^T_iR_ie_{ij})\tag5 E(Ci,Ci′)=j∈N(i)∑wij(eij′−Rieij)2=j∈N(i)∑wij(eij′Teij′−eij′TRieij+eijTRiTRieij)(5)
因为 R R R是旋转矩阵(正交矩阵), R i T R i = I R^T_iR_i = I RiTRi=I, 所以上式等于:
E ( C i , C i ′ ) = ∑ j ∈ N ( i ) w i j ( e i j ′ T e i j ′ − e i j ′ T R i e i j + e i j T e i j ) (6) E(C_i,C_i' )=\sum_{j\in N(i)}w_{ij}(e'^T_{ij}e'_{ij}-e'^T_{ij}R_ie_{ij}+e^T_{ij}e_{ij})\tag6 E(Ci,Ci′)=j∈N(i)∑wij(eij′Teij′−eij′TRieij+eijTeij)(6)
上式的最小值跟不含 R i R_i Ri的项无关,因此:
R i = arg min R i ∑ j ∈ N ( i ) w i j ( − e i j ′ T R i e i j ) = arg max R i ∑ j ∈ N ( i ) w i j e i j ′ T R i e i j (7) R_i = \argmin \limits_{R_i}\sum_{j\in N(i)}w_{ij}(-e'^T_{ij}R_ie_{ij}) = \argmax \limits_{R_i}\sum_{j\in N(i)}w_{ij}e'^T_{ij}R_ie_{ij}\tag7 Ri=Riargminj∈N(i)∑wij(−eij′TRieij)=Riargmaxj∈N(i)∑wijeij′TRieij(7)
上式可以写成矩阵的迹的形式(参见末尾示意图)进行改写:
R i = arg max R i T r ( ∑ j ∈ N ( i ) w i j R i e i j e i j ′ T ) (8) R_i =\argmax \limits_{R_i}Tr(\sum_{j\in N(i)}w_{ij}R_ie_{ij}e'^T_{ij}) \tag8 Ri=RiargmaxTr(j∈N(i)∑wijRieijeij′T)(8)
并将 R i R_i Ri提到外面:
R i = arg max R i T r ( R i ∑ j ∈ N ( i ) w i j e i j e i j ′ T ) (9) R_i =\argmax \limits_{R_i}Tr(R_i\sum_{j\in N(i)}w_{ij}e_{ij}e'^T_{ij})\tag9 Ri=RiargmaxTr(Rij∈N(i)∑wijeijeij′T)(9)
接下来就是如何求解这个旋转矩阵,假设 S i = ∑ j ∈ N ( i ) w i j e i j e i j ′ T S_i = \sum_{j\in N(i)}w_{ij}e_{ij}e'^T_{ij} Si=∑j∈N(i)wijeijeij′T, 一般而言, S i S_i Si 可以通过奇异值分解得到:
S i = U i Σ i V i T (10) S_i = U_i\Sigma_iV^T_i\tag{10} Si=UiΣiViT(10)
那么(9)可以进一步写为:
R i = arg max R i T r ( R i U i Σ i V i T ) (11) R_i =\argmax \limits_{R_i}Tr(R_iU_i\Sigma_iV^T_i) \tag{11} Ri=RiargmaxTr(RiUiΣiViT)(11)
根据 T r ( A B ) = T r ( B A ) Tr(AB) = Tr(BA) Tr(AB)=Tr(BA),上式进一步改写:
R i = arg max R i T r ( V i T R i U i Σ i ) (12) R_i =\argmax \limits_{R_i}Tr(V^T_iR_iU_i\Sigma_i) \tag{12} Ri=RiargmaxTr(ViTRiUiΣi)(12)
令: X = V i T R i U i X = V^T_iR_iU_i X=ViTRiUi, 因为此三个矩阵都是正交矩阵,所以 X X X也是正交矩阵,上式可以写成:
R i = arg max R i T r ( X Σ i ) (13) R_i =\argmax \limits_{R_i}Tr(X\Sigma_i) \tag{13} Ri=RiargmaxTr(XΣi)(13)
而:
T r ( X Σ i ) = X ( 1 , 1 ) Σ i ( 1 , 1 ) + X ( 2 , 2 ) Σ i ( 2 , 2 ) + X ( 3 , 3 ) Σ i ( 3 , 3 ) (14) Tr(X\Sigma_i) = X_{(1,1)}\Sigma_i(1,1) + X_{(2,2)}\Sigma_i(2,2) + X_{(3,3)}\Sigma_i(3,3)\tag {14} Tr(XΣi)=X(1,1)Σi(1,1)+X(2,2)Σi(2,2)+X(3,3)Σi(3,3)(14)
对于上式有两点需要注意:
1) Σ i \Sigma_i Σi保存了矩阵 S i S_i Si的所有奇异值,所以 Σ i \Sigma_i Σi的对角线上的元素均大于等于0(奇异值分解的性质决定)。
2)另外,正交矩阵中的各元素的取值 X ( i , j ) ∈ [ 0 , 1 ] X_{(i,j)} \in [0,1] X(i,j)∈[0,1]。
因此,当X是单位阵时上式取得最大值,即 Σ i \Sigma_i Σi对角线元素之和。因此只需要 X = V i T R i U i = I X= V^T_iR_iU_i=I X=ViTRiUi=I 即可,所以:
R i = V i U i T (15) R_i = V_iU^T_i\tag{15} Ri=ViUiT(15)
这就是论文给出的最终的旋转矩阵的求解方法。
三、已知 R R R求解变形后的顶点 P ′ P' P′
这一步相对比较简单,直接对能量函数求导即可,具体推导就把论文中搬出来即可:
∂ E ( S ′ ) ∂ p i ′ = ∂ ∂ p i ′ ( ∑ j ∈ N ( i ) w i j ∥ ( p i ′ − p j ′ ) − R i ( p i − p j ) ∥ 2 + ∑ j ∈ N ( i ) w j i ∥ ( p j ′ − p i ′ ) − R j ( p j − p i ) ∥ 2 ) = = ∑ j ∈ N ( i ) 2 w i j ( ( p i ′ − p j ′ ) − R i ( p i − p j ) ) + + ∑ j ∈ N ( i ) − 2 w j i ( ( p j ′ − p i ′ ) − R j ( p j − p i ) ) . (16) \begin{aligned} \frac{\partial E\left(\mathcal{S}^{\prime}\right)}{\partial \mathbf{p}_{i}^{\prime}} &=\frac{\partial}{\partial \mathbf{p}_{i}^{\prime}}\left(\sum_{j \in \mathcal{N}(i)} w_{i j}\left\|\left(\mathbf{p}_{i}^{\prime}-\mathbf{p}_{j}^{\prime}\right)-\mathbf{R}_{i}\left(\mathbf{p}_{i}-\mathbf{p}_{j}\right)\right\|^{2}\right.\\ &\left.+\sum_{j \in \mathcal{N}(i)} w_{j i}\left\|\left(\mathbf{p}_{j}^{\prime}-\mathbf{p}_{i}^{\prime}\right)-\mathbf{R}_{j}\left(\mathbf{p}_{j}-\mathbf{p}_{i}\right)\right\|^{2}\right)=\\ &=\sum_{j \in \mathcal{N}(i)} 2 w_{i j}\left(\left(\mathbf{p}_{i}^{\prime}-\mathbf{p}_{j}^{\prime}\right)-\mathbf{R}_{i}\left(\mathbf{p}_{i}-\mathbf{p}_{j}\right)\right)+\\ &+\sum_{j \in \mathcal{N}(i)}-2 w_{j i}\left(\left(\mathbf{p}_{j}^{\prime}-\mathbf{p}_{i}^{\prime}\right)-\mathbf{R}_{j}\left(\mathbf{p}_{j}-\mathbf{p}_{i}\right)\right) . \end{aligned}\tag{16} ∂pi′∂E(S′)=∂pi′∂⎝ ⎛j∈N(i)∑wij∥ ∥(pi′−pj′)−Ri(pi−pj)∥ ∥2+j∈N(i)∑wji∥ ∥(pj′−pi′)−Rj(pj−pi)∥ ∥2⎠ ⎞==j∈N(i)∑2wij((pi′−pj′)−Ri(pi−pj))++j∈N(i)∑−2wji((pj′−pi′)−Rj(pj−pi)).(16)
因为 w i j = w j i w_{ij} = w_{ji} wij=wji, 上式进一步改写为:
∂ E ( S ′ ) ∂ p i ′ = ∑ j ∈ N ( i ) 4 w i j ( ( p i ′ − p j ′ ) − 1 2 ( R i + R j ) ( p i − p j ) ) \frac{\partial E\left(\mathcal{S}^{\prime}\right)}{\partial \mathbf{p}_{i}^{\prime}}=\sum_{j \in \mathcal{N}(i)} 4 w_{i j}\left(\left(\mathbf{p}_{i}^{\prime}-\mathbf{p}_{j}^{\prime}\right)-\frac{1}{2}\left(\mathbf{R}_{i}+\mathbf{R}_{j}\right)\left(\mathbf{p}_{i}-\mathbf{p}_{j}\right)\right) ∂pi′∂E(S′)=j∈N(i)∑4wij((pi′−pj′)−21(Ri+Rj)(pi−pj))
令导数为0,则可以得到:
∑ j ∈ N ( i ) w i j ( p i ′ − p j ′ ) = ∑ j ∈ N ( i ) w i j 2 ( R i + R j ) ( p i − p j ) (17) \sum_{j \in \mathcal{N}(i)} w_{i j}\left(\mathbf{p}_{i}^{\prime}-\mathbf{p}_{j}^{\prime}\right)=\sum_{j \in \mathcal{N}(i)} \frac{w_{i j}}{2}\left(\mathbf{R}_{i}+\mathbf{R}_{j}\right)\left(\mathbf{p}_{i}-\mathbf{p}_{j}\right) \tag{17} j∈N(i)∑wij(pi′−pj′)=j∈N(i)∑2wij(Ri+Rj)(pi−pj)(17)
最终转换为一个线性方程组求解即可。
四、补充:(7)式到(8)式,矩阵到迹的表示
可令(7)式中的 A = w i j e i j ′ T , B = R i e i j A = w_{ij}e'^T_{ij}, B = R_ie_{ij} A=wijeij′T,B=Rieij, 其中A是一行3列,B是3行一列,对于这种行矩阵跟列矩阵的乘法可以表示为矩阵的迹,下面展示了更一般的情况: A 1 × n B n × 1 = T r ( B n × 1 A 1 × n ) A_{1\times n}B_{n\times 1} = Tr(B_{n\times 1}A_{1\times n}) A1×nBn×1=Tr(Bn×1A1×n)。

参考资料:
[1] 知乎:用数学编辑3D模型(二)- As-Rigid-As-Possible
[2] 知乎:奇异值分解(SVD)
[3] 矩阵迹的性质和运算
[4] http://blog.csdn.net/seamanj/article/details/50597420 (Tr(M) >= Tr(RM))