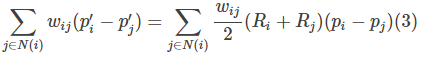欢迎关注更多精彩
关注我,学习常用算法与数据结构,一题多解,降维打击。

rarp变形全称是 As-Rigid-As-Possible Suface Deformation.
意思是变形时尽量使每条边保持一个钢性变换。基本思路是基于能量优化来做。
能量定义
E = ∑ i = 1 N v w i ∑ j ∈ Ω ( i ) w i j ∣ ∣ ( p i ′ − p j ′ ) − R i ( p i − p j ) ∣ ∣ 2 E=\displaystyle \sum ^{N_v}_{i=1}w_i \displaystyle \sum_{j\in \Omega(i)}w_{ij}||(p'_i-p'_j)-R_i(p_i-p_j)||^2 E=i=1∑Nvwij∈Ω(i)∑wij∣∣(pi′−pj′)−Ri(pi−pj)∣∣2
w i 可 取 邻 域 面 积 , w i j 可 以 取 c o t 权 , 实 际 实 现 是 取 1 w_i可取邻域面积,w_{ij}可以取cot权,实际实现是取1 wi可取邻域面积,wij可以取cot权,实际实现是取1
其 中 变 量 是 p i ′ 和 R i 其中变量是p'_i和R_i 其中变量是pi′和Ri
上述式子意思是尽量让每边的变化尽量是一个旋转变化。
求解过程
基本思路是通过local/global 交替迭代法来做。
Local部分
给 定 p i ′ , 计 算 R i 给定p'_i, 计算R_i 给定pi′,计算Ri
每一个点的能量可以单独计算,对于第i个点计算如下。
E i = ∑ j ∈ Ω ( i ) w i j ∣ ∣ ( p i ′ − p j ′ ) − R i ( p i − p j ) ∣ ∣ 2 E_i=\displaystyle \sum_{j\in \Omega(i)}w_{ij}||(p'_i-p'_j)-R_i(p_i-p_j)||^2 Ei=j∈Ω(i)∑wij∣∣(pi′−pj′)−Ri(pi−pj)∣∣2
令 e i j ′ = p i ′ − p j ′ , e i j = p i − p j 令e'_{ij}=p'_i-p'_j, e_{ij}=p_i-p_j 令eij′=pi′−pj′,eij=pi−pj
∴ E i = ∑ j ∈ Ω ( i ) w i j ∣ ∣ e i j ′ − R i e i j ∣ ∣ 2 \therefore E_i=\displaystyle \sum_{j\in \Omega(i)}w_{ij}||e'_{ij}-R_ie_{ij}||^2 ∴Ei=j∈Ω(i)∑wij∣∣eij′−Rieij∣∣2
= ∑ j ∈ Ω ( i ) w i j ( e i j ′ − R i e i j ) T ( e i j ′ − R i e i j ) =\displaystyle \sum_{j\in \Omega(i)}w_{ij}(e'_{ij}-R_ie_{ij})^T(e'_{ij}-R_ie_{ij}) =j∈Ω(i)∑wij(eij′−Rieij)T(eij′−Rieij)
= ∑ j ∈ Ω ( i ) w i j ( e i j ′ T e i j ′ − 2 e i j ′ T R i e i j + e i j T R i T R i e i j ) =\displaystyle \sum_{j\in \Omega(i)}w_{ij}(e'^T_{ij}e'_{ij}-2e'^T_{ij}R_ie_{ij}+e^T_{ij}R^T_iR_ie_{ij}) =j∈Ω(i)∑wij(eij′Teij′−2eij′TRieij+eijTRiTRieij)
∵ R i T R i 是 单 位 矩 阵 \because R^T_iR_i 是单位矩阵 ∵RiTRi是单位矩阵
∴ = ∑ j ∈ Ω ( i ) w i j ( e i j ′ T e i j ′ − 2 e i j ′ T R i e i j + e i j T e i j ) \therefore =\displaystyle \sum_{j\in \Omega(i)}w_{ij}(e'^T_{ij}e'_{ij}-2e'^T_{ij}R_ie_{ij}+e^T_{ij}e_{ij}) ∴=j∈Ω(i)∑wij(eij′Teij′−2eij′TRieij+eijTeij)
由于Ri是变量,前后两项是常量。只要优化中间项即可
a r g m i n R i ∑ j ∈ Ω ( i ) − w i j 2 e i j ′ T R i e i j arg\;\underset{R_i}{min} \displaystyle \sum_{j \in \Omega(i)}-w_{ij}2e'^T_{ij}R_ie_{ij} argRiminj∈Ω(i)∑−wij2eij′TRieij
负的最小,就是正的最大。去负号
= a r g m a x R i ∑ j ∈ Ω ( i ) w i j 2 e i j ′ T R i e i j =arg\;\underset{R_i}{max} \displaystyle \sum_{j \in \Omega(i)}w_{ij}2e'^T_{ij}R_ie_{ij} =argRimaxj∈Ω(i)∑wij2eij′TRieij
= a r g m a x R i T r ( ∑ j ∈ Ω ( i ) w i j R i e i j e i j ′ T ) =arg\;\underset{R_i}{max} \;Tr \left ( \displaystyle \sum_{j \in \Omega(i)}w_{ij}R_ie_{ij}e'^T_{ij} \right ) =argRimaxTr⎝⎛j∈Ω(i)∑wijRieijeij′T⎠⎞
= a r g m a x R i T r ( R i ∑ j ∈ Ω ( i ) w i j e i j e i j ′ T ) ( ∗ ) =arg\;\underset{R_i}{max} \;Tr \left ( R_i \displaystyle \sum_{j \in \Omega(i)}w_{ij}e_{ij}e'^T_{ij} \right )(*) =argRimaxTr⎝⎛Rij∈Ω(i)∑wijeijeij′T⎠⎞(∗)
令 S i = ∑ j ∈ Ω ( i ) w i j e i j e i j ′ T ( 都 是 常 量 ) , S i = U i ∑ i V i T ( S V D 分 解 ) 令S_i = \displaystyle \sum_{j \in \Omega(i)}w_{ij}e_{ij}e'^T_{ij}(都是常量), S_i = U_i \sum_iV^T_i (SVD分解) 令Si=j∈Ω(i)∑wijeijeij′T(都是常量),Si=Uii∑ViT(SVD分解)
根据定理:如果 M是一个对称正定矩阵,那么对于任意正交矩阵R
Tr(M)>Tr(RM)。
只 有 当 R i 是 对 称 正 定 矩 阵 时 ( ∗ ) 取 最 优 值 , 故 R i = V i U i T 只有当R_i是对称正定矩阵时(*)取最优值,故R_i = V_iU^T_i 只有当Ri是对称正定矩阵时(∗)取最优值,故Ri=ViUiT
当Ri的行列式值小于0时,需要对第三列取相反数。
Global部分
给 定 R i , 计 算 p i ′ 给定R_i, 计算p'_i 给定Ri,计算pi′
文 章 中 说 对 E 进 行 p i ′ 求 偏 导 可 以 得 到 文章中说对E进行p'_i求偏导可以得到 文章中说对E进行pi′求偏导可以得到
∂ E ∂ p i ′ = ∑ j ∈ Ω ( i ) ( ( p i ′ − p j ′ ) − 1 2 ( R i + R j ) ( p i − p j ) ) \frac {\partial E}{\partial p'_i}=\displaystyle \sum_{j\in \Omega(i)} \left((p'_i-p'_j) -\frac{1}{2}(R_i+R_j)(p_i - p_j) \right) ∂pi′∂E=j∈Ω(i)∑((pi′−pj′)−21(Ri+Rj)(pi−pj))
文章中没有解释为什么。我这边自己推导一下。
当 我 们 对 p i ′ 求 导 时 , 跟 p i ′ 无 关 的 式 子 结 果 就 是 0 , 那 有 关 的 是 哪 些 呢 。 当我们对p'_i求导时,跟p'_i无关的式子结果就是0,那有关的是哪些呢。 当我们对pi′求导时,跟pi′无关的式子结果就是0,那有关的是哪些呢。
有 关 的 是 E i = ∑ j ∈ Ω ( i ) w i j ∣ ∣ ( p i ′ − p j ′ ) − R i ( p i − p j ) ∣ ∣ 2 , 以 及 E j 中 和 i 相 关 的 。 有关的是 E_i=\displaystyle \sum_{j\in \Omega(i)}w_{ij}||(p'_i-p'_j)-R_i(p_i-p_j)||^2,以及E_j中和i相关的。 有关的是Ei=j∈Ω(i)∑wij∣∣(pi′−pj′)−Ri(pi−pj)∣∣2,以及Ej中和i相关的。
不 难 发 现 每 一 个 w i j ∣ ∣ ( p i ′ − p j ′ ) − R i ( p i − p j ) ∣ ∣ 2 肯 定 有 一 个 对 应 的 反 向 式 子 。 不难发现每一个w_{ij}||(p'_i-p'_j)-R_i(p_i-p_j)||^2肯定有一个对应的反向式子。 不难发现每一个wij∣∣(pi′−pj′)−Ri(pi−pj)∣∣2肯定有一个对应的反向式子。
w j i ∣ ∣ ( p j ′ − p i ′ ) − R j ( p j − p i ) ∣ ∣ 2 w_{ji}||(p'_j-p'_i)-R_j(p_j-p_i)||^2 wji∣∣(pj′−pi′)−Rj(pj−pi)∣∣2
记 ∂ i = ∑ j ∈ Ω ( i ) ( w i j ∣ ∣ ( p i ′ − p j ′ ) − R i ( p i − p j ) ∣ ∣ 2 + w j i ∣ ∣ ( p j ′ − p i ′ ) − R j ( p j − p i ) ∣ ∣ 2 ) 记\partial i = \displaystyle \sum_{j\in \Omega(i)}(w_{ij}||(p'_i-p'_j)-R_i(p_i-p_j)||^2+w_{ji}||(p'_j-p'_i)-R_j(p_j-p_i)||^2) 记∂i=j∈Ω(i)∑(wij∣∣(pi′−pj′)−Ri(pi−pj)∣∣2+wji∣∣(pj′−pi′)−Rj(pj−pi)∣∣2)
∴ ∂ E ∂ p i ′ = ∂ i ∂ p i ′ = ∑ j ∈ Ω ( i ) ( 2 w i j [ ( p i ′ − p j ′ ) − R i ( p i − p j ) ] + 2 w j i [ ( p j ′ − p i ′ ) − R j ( p j − p i ) ] ) \therefore \frac {\partial E}{\partial p'_i}=\frac {\partial i}{\partial p'_i}=\displaystyle \sum_{j\in \Omega(i)}(2w_{ij}\left[(p'_i-p'_j)-R_i(p_i-p_j)\right]+2w_{ji}[(p'_j-p'_i)-R_j(p_j-p_i)]) ∴∂pi′∂E=∂pi′∂i=j∈Ω(i)∑(2wij[(pi′−pj′)−Ri(pi−pj)]+2wji[(pj′−pi′)−Rj(pj−pi)])
∵ w i j = w j i , i , j 也 可 以 互 换 \because w_{ij}=w_{ji}, i,j也可以互换 ∵wij=wji,i,j也可以互换
∴ ∂ E ∂ p i ′ = ∑ j ∈ Ω ( i ) ( 2 w i j [ ( p i ′ − p j ′ ) − R i ( p i − p j ) ] + 2 w i j [ ( p i ′ − p j ′ ) − R j ( p i − p j ) ] ) \therefore \frac {\partial E}{\partial p'_i}=\displaystyle \sum_{j\in \Omega(i)}(2w_{ij}\left[(p'_i-p'_j)-R_i(p_i-p_j)\right]+2w_{ij}[(p'_i-p'_j)-R_j(p_i-p_j)]) ∴∂pi′∂E=j∈Ω(i)∑(2wij[(pi′−pj′)−Ri(pi−pj)]+2wij[(pi′−pj′)−Rj(pi−pj)])
= ∑ j ∈ Ω ( i ) w i j [ 4 ( p i ′ − p j ′ ) − 2 ( R i + R i ) ( p i − p j ) ] =\displaystyle \sum_{j\in \Omega(i)}w_{ij}[4(p'_i-p'_j)-2(R_i+R_i)(p_i-p_j)] =j∈Ω(i)∑wij[4(pi′−pj′)−2(Ri+Ri)(pi−pj)]
= ∑ j ∈ Ω ( i ) 4 w i j [ ( p i ′ − p j ′ ) − 1 2 ( R i + R i ) ( p i − p j ) ] =\displaystyle \sum_{j\in \Omega(i)}4w_{ij}\left[(p'_i-p'_j)-\frac 1 2(R_i+R_i)(p_i-p_j)\right] =j∈Ω(i)∑4wij[(pi′−pj′)−21(Ri+Ri)(pi−pj)]
令上式等于0,整理一下将常数项移到右边,得到第i行等式如下
∑ j ∈ Ω ( i ) w i j ( p i ′ − p j ′ ) = ∑ j ∈ Ω ( i ) w i j 2 ( R i + R i ) ( p i − p j ) \displaystyle \sum_{j\in \Omega(i)}w_{ij}(p'_i-p'_j) =\displaystyle \sum_{j\in \Omega(i)} \frac {w_{ij}} 2(R_i+R_i)(p_i-p_j) j∈Ω(i)∑wij(pi′−pj′)=j∈Ω(i)∑2wij(Ri+Ri)(pi−pj)
= > ( ∑ j ∈ Ω ( i ) w i j ) p i ′ − ∑ j ∈ Ω ( i ) w i j p j ′ = ∑ j ∈ Ω ( i ) w i j 2 ( R i + R i ) ( p i − p j ) =>\left(\displaystyle \sum_{j\in \Omega(i)}w_{ij}\right)p'_i-\displaystyle \sum_{j\in \Omega(i)}w_{ij}p'_j =\displaystyle \sum_{j\in \Omega(i)} \frac {w_{ij}} 2(R_i+R_i)(p_i-p_j) =>⎝⎛j∈Ω(i)∑wij⎠⎞pi′−j∈Ω(i)∑wijpj′=j∈Ω(i)∑2wij(Ri+Ri)(pi−pj)
代码实现
代码库:https://github.com/LightningBilly/ACMAlgorithms/tree/master/图形学算法/三角网格算法/ARAP Deformation/
#include "glew/2.2.0_1/include/GL/glew.h"
#include "glfw/3.3.4/include/GLFW/glfw3.h"
#include <iostream>
#include <cmath>
#include "IOManager.h"
#include <cmath>
#include <limits.h>
#include <set>
#include <numeric>
#include<Eigen/SVD>
#include<Eigen/Dense>
#include<Eigen/Sparse>using namespace std;#define ColoredVertex(c,v) do{ glColor3fv(c); glVertex3fv(v); }while(0)char *path = "/Users/bytedance/CLionProjects/glTriangle/cow.obj";
// char *path = "/Users/bytedance/CLionProjects/glTriangle/input_1.obj";
void arap_deformation();
PolyMesh * mesh;int motion_mode = 0;//set fix handle
//set<int> handles_f = {12,505,381,712,296};
set<int> handles_f;//set move handle
//vector<int> handles_m = {652};
//vector<MVector3> handles_m_pos = { MVector3(0.05,0.2,0.05) };
vector<int> handles_m;
vector<MVector3> handles_m_pos;void key_callback(GLFWwindow* window, int key, int scancode, int action, int mode)
{//如果按下ESC,把windowShouldClose设置为True,外面的循环会关闭应用if(key==GLFW_KEY_ESCAPE && action == GLFW_PRESS) {glfwSetWindowShouldClose(window, GL_TRUE);std::cout << "ESC" << mode;}if (action != GLFW_PRESS)return;switch (key){case GLFW_KEY_ESCAPE:glfwSetWindowShouldClose(window, GL_TRUE);break;case GLFW_KEY_1:{cout<<GLFW_KEY_1<<endl;}break;default:break;}cout<<"isd: "<<isdigit(key)<<endl;if(isdigit(key)) motion_mode=key;}int moving = 0;
double sx=0, sy=0, angy=0, angx=0;
MPoint3 st;void mouse_click(GLFWwindow* window, int button, int action, int mods) {cout<<"m : "<<motion_mode<<endl;cout<<button<<","<<action<<","<<mods<<endl;double xpos, ypos;glfwGetCursorPos(window, &xpos, &ypos);// cout<<xpos/300-1<<","<<1-ypos/300<<endl;switch (motion_mode) {case GLFW_KEY_1:sx = xpos;sy = ypos;moving = action;break;case GLFW_KEY_2: // 选择固定点if(action==0){auto si=mesh->getNearPoint(MPoint3(xpos/300-1, 1-ypos/300, 0));if(si>=0) {handles_f.insert(si);}}break;case GLFW_KEY_3: // 选择移动点if(action==0){auto si=mesh->getNearPoint(MPoint3(xpos/300-1, 1-ypos/300, 0));if(si>=0) {handles_m.push_back(si);}}break;case GLFW_KEY_4: // 选择移动点if(action==1){st = MPoint3(xpos/300-1, 1-ypos/300, 0);} else {MVector3 v = MPoint3(xpos/300-1, 1-ypos/300, 0) - st;handles_m_pos.assign(handles_m.size(), MPoint3());for(int i=0;i<handles_m.size();i++) {handles_m_pos[i] = mesh->vert(handles_m[i])->position()+v;}arap_deformation();}break;}}MVector3 cal_circum_enter(const MVector3& a, const MVector3& b, const MVector3& c)
{MVector3 ac = c - a, ab = b - a;MVector3 abXac = cross(ab, ac), abXacXab = cross(abXac, ab), acXabXac = cross(ac, abXac);return a + (abXacXab * ac.normSq() + acXabXac * ab.normSq()) / (2.0 * abXac.normSq());
}void cal_local_ave_region(std::vector<double> &vertexLAR)
{vertexLAR.assign(mesh->numVertices(), 0);for(auto v:mesh->vertices()) {auto ps = mesh->vertAdjacentPolygon(v);if(ps.size()==0)continue;auto n = ps[0]->normal();for(int i=1;i<ps.size();i++) n+=ps[i]->normal();n/=ps.size();//v->setNormal(n);}for (MPolyFace* fh : mesh->polyfaces()){// judge if it's obtusebool isObtuseAngle = false;MVert *obtuseVertexHandle;MHalfedge *he = fh->halfEdge();MHalfedge *he_next = he->next(), *he_prev = he->prev();MVert *v_from_he = he->fromVertex(), *v_from_he_next = he_next->fromVertex(), *v_from_he_prev = he_prev->fromVertex();MVector3 vec_he_nor = he->tangent(), vec_he_next_nor = he_next->tangent(), vec_he_prev_nor = he_prev->tangent();if (vectorAngle(vec_he_nor, -vec_he_prev_nor) > M_PI / 2.0){isObtuseAngle = true;obtuseVertexHandle = v_from_he;}else if (vectorAngle(vec_he_next_nor, -vec_he_nor) > M_PI / 2.0){isObtuseAngle = true;obtuseVertexHandle = v_from_he_next;}else if (vectorAngle(vec_he_prev_nor, -vec_he_next_nor) > M_PI / 2.0){isObtuseAngle = true;obtuseVertexHandle = v_from_he_prev;}// calculate areaif (isObtuseAngle){double faceArea = 0.5*norm(cross(v_from_he_next->position() - v_from_he->position(), v_from_he_prev->position() - v_from_he->position()));for (MVert* fv : mesh->polygonVertices(fh)){if (fv == obtuseVertexHandle)vertexLAR[fv->index()] += faceArea / 2.0;elsevertexLAR[fv->index()] += faceArea / 4.0;}}else{MVector3 cc = cal_circum_enter(v_from_he->position(), v_from_he_next->position(), v_from_he_prev->position());for (MHalfedge* fhh : mesh->polygonHalfedges(fh)){MVector3 edgeMidpoint = 0.5*(fhh->fromVertex()->position() + fhh->toVertex()->position());double edgeLength = fhh->edge()->length();double partArea = 0.5 * edgeLength * (edgeMidpoint - cc).norm();vertexLAR[fhh->fromVertex()->index()] += 0.5*partArea;vertexLAR[fhh->toVertex()->index()] += 0.5*partArea;}}}
}void cal_gaussian_curvature(const std::vector<double> &vertexLAR,std::vector<double> &gaussianCur)
{gaussianCur.assign(mesh->numVertices(), 0);for (MVert* vh : mesh->vertices()){double angle_temp = 2 * M_PI;MVector3 p_vh = vh->position();for (auto voh_it = mesh->voh_iter(vh); voh_it.isValid(); ++voh_it){if (!(*voh_it)->isBoundary()){MHalfedge* next_voh = (*voh_it)->next();MVert* to_voh = (*voh_it)->toVertex(), *to_next_voh = next_voh->toVertex();MVector3 p_to_voh = to_voh->position(), p_to_next_voh = to_next_voh->position();double angle = vectorAngle(p_to_voh - p_vh, p_to_next_voh - p_vh);angle_temp -= angle;}}angle_temp /= vertexLAR[vh->index()];gaussianCur[vh->index()] = angle_temp;}std::cout << "Calculate Gaussian Curvature Done" << std::endl;
}void calc_cot_weight(vector<double>& cots)
{cots.clear();cots.resize(mesh->numHalfEdges(), 0.);for (auto ithe = mesh->halfedge_begin(); ithe != mesh->halfedge_end(); ithe++){if (mesh->isBoundary(*ithe))continue;auto v0=(*ithe)->fromVertex()->position();auto v1 = (*ithe)->toVertex()->position();auto v2 = (*ithe)->next()->toVertex()->position();auto e0 = v0 - v2;auto e1 = v1 - v2;double cotangle = dot(e0,e1) / cross(e0,e1).norm();
// cots[ithe->idx()] = cotangle;cots[(*ithe)->index()] = 1.;}
}void arap_deformation()
{int nf = mesh->numPolygons();int nv = mesh->numVertices();//position backupvector<MVector3> pos_mesh_ref;pos_mesh_ref.resize(nv);for (auto itv : mesh->vertices()){pos_mesh_ref[itv->index()] = itv->position();}vector<double> cots;calc_cot_weight(cots);set<int> handles = handles_f;handles.insert(handles_m.begin(), handles_m.end());//calc cot-weight laplacian matrixvector<Eigen::Triplet<double>> trivec;// 根据求导公式将左边填充for (int i = 0; i < nv; i++){// 固定点直接将该点参数填1if (handles.count(i) > 0){trivec.emplace_back(i, i, 1.);continue;}auto v_h = mesh->vert(i);double weight_sum = 0.;for (auto itvoh = mesh->voh_iter(v_h); itvoh.isValid(); ++itvoh){auto v_to_h = (*itvoh)->toVertex();double weight_ = cots[(*itvoh)->index()] + cots[(*itvoh)->pair()->index()];weight_sum += weight_;trivec.emplace_back(i, v_to_h->index(), -weight_);}trivec.emplace_back(i, i, weight_sum);}Eigen::SparseMatrix<double> smat;smat.resize(nv, nv);smat.setFromTriplets(trivec.begin(),trivec.end());Eigen::SparseLU<Eigen::SparseMatrix<double>> solver;solver.compute(smat);Eigen::MatrixX3d uv;uv.resize(nv, 3);vector<Eigen::Matrix3d> Lts;Lts.resize(nv);Eigen::MatrixX3d b;b.resize(nv, 3);//local-global iterationfor (int iter = 0; iter < 10; iter++){//local calc Lt
#pragma omp parallel forfor (int i = 0; i < nv; i++){auto v_h = mesh->vert(i);Eigen::Matrix3d J = Eigen::Matrix3d::Zero();for (auto itvoh = mesh->voh_iter(v_h); itvoh.isValid(); ++itvoh){auto v_to_h = (*itvoh)->toVertex();auto e_ = pos_mesh_ref[i] - pos_mesh_ref[v_to_h->index()];auto ep_ = v_h->position() - v_to_h->position();double weight_ = cots[(*itvoh)->index()] + cots[(*itvoh)->pair()->index()];Eigen::Vector3d ep(ep_[0], ep_[1], ep_[2]);Eigen::Vector3d e(e_[0], e_[1], e_[2]);J += weight_ * (e*ep.transpose());}Eigen::JacobiSVD<Eigen::Matrix3d> svd(J, Eigen::ComputeFullU| Eigen::ComputeFullV);Eigen::Matrix3d U = svd.matrixU();Eigen::Matrix3d V = svd.matrixV();Eigen::Matrix3d R = V * U.transpose();if (R.determinant() < 0){U(0, 2) *= -1;U(1, 2) *= -1;U(2, 2) *= -1;R = V * U.transpose();}Lts[i] = R;}//global calc b
#pragma omp parallel forfor (int i = 0; i < nv; i++){auto v_h = mesh->vert(i);Eigen::Vector3d b_tmp(0., 0., 0.);for (auto itvoh = mesh->voh_iter(v_h); itvoh.isValid(); ++itvoh){auto v_to_h = (*itvoh)->toVertex();auto ep_ = pos_mesh_ref[i] - pos_mesh_ref[v_to_h->index()];Eigen::Vector3d ep(ep_[0], ep_[1], ep_[2]);Eigen::Matrix3d JR = Lts[i] + Lts[v_to_h->index()];double weight_ = (cots[(*itvoh)->index()] + cots[(*itvoh)->pair()->index()]) / 2.0;b_tmp += weight_ * (JR*ep);}b(i, 0) = b_tmp[0];b(i, 1) = b_tmp[1];b(i, 2) = b_tmp[2];}//set handlesfor (int i:handles_f){auto b_tmp = pos_mesh_ref[i];b(i, 0) = b_tmp[0];b(i, 1) = b_tmp[1];b(i, 2) = b_tmp[2];}for (int i = 0; i < handles_m.size(); i++){auto b_tmp = handles_m_pos[i];b(handles_m[i], 0) = b_tmp[0];b(handles_m[i], 1) = b_tmp[1];b(handles_m[i], 2) = b_tmp[2];}//global solveuv.col(0) = solver.solve(b.col(0));uv.col(1) = solver.solve(b.col(1));uv.col(2) = solver.solve(b.col(2));#pragma omp parallel forfor (int i = 0; i < nv; i++){auto v_h = mesh->vert(i);v_h->setPosition(uv(i, 0), uv(i, 1), uv(i, 2));}}}int lastse = -1;int main(void) {auto r = new OBJReader();string writePath = "/Users/bytedance/CLionProjects/glTriangle/d1.txt";mesh = new PolyMesh();r->read(path, mesh);std::vector<double> gaussianCur;std::vector<double> vertexLAR;cal_local_ave_region(vertexLAR);cal_gaussian_curvature(vertexLAR, gaussianCur);// mesh->scale(0.5);mesh->scale(1);double m = *max_element(gaussianCur.begin(), gaussianCur.end());/*for(int i=0;i<gaussianCur.size();i++) {gaussianCur[i]=gaussianCur[i]*1000/m;cout<<gaussianCur[i]<<endl;}*//*auto w = new OBJWriter();w->write(writePath, mesh);*///初始化GLFW库if (!glfwInit())return -1;//创建窗口以及上下文GLFWwindow *window = glfwCreateWindow(600, 600, "hello world", NULL, NULL);if (!window) {//创建失败会返回NULLglfwTerminate();}//建立当前窗口的上下文glfwMakeContextCurrent(window);glfwSetKeyCallback(window, key_callback); //注册回调函数glfwSetMouseButtonCallback(window, mouse_click);//glViewport(0, 0, 400, 400);//gluOrtho2D(-200, 200.0, -200, 200.0);//循环,直到用户关闭窗口while (!glfwWindowShouldClose(window)) {/*******轮询事件*******/glfwPollEvents();// cout<<456<<endl;//选择清空的颜色RGBAdouble xpos, ypos;glfwGetCursorPos(window, &xpos, &ypos);if ( ypos>0 && xpos>0&&(fabs(ypos -sy)>1 || (fabs(xpos -sx)>1))) {if(moving) {cout << "cur p" << xpos << "," << ypos << endl;angy += (sy - ypos) / 300 * 360 + 360;while (angy >= 360) angy -= 360;cout << "angley:" << angy << endl;angx += (sx - xpos) / 300 * 360 + 360;while (angx >= 360) angx -= 360;cout << "anglex:" << angx << endl;}sx = xpos;sy = ypos;// cout<<"select"<<endl;auto si=mesh->getNearPoint(MPoint3(xpos/300-1, 1-ypos/300, 0));if(si!=lastse && lastse>=0) mesh->vert(lastse)->setSelected(false);if(si>=0) {lastse=si;// cout<<"666 "<<si<<endl;mesh->vert(si)->setSelected(true);}}for(auto i: handles_f) {mesh->vert(i)->setSelected(true);}for(auto i: handles_m) {mesh->vert(i)->setSelected(true);}/*sx = xpos/300-1;sy = -(ypos/300-1);*/glClearColor(0, 0, 0, 1);// glColor3f(0,0, 0);glMatrixMode(GL_PROJECTION);glEnable(GL_DEPTH_TEST);glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);mesh->Draw(angy, angx, gaussianCur);angy = 0, angx=0;for (int i=0, n=1000; i<n;i++) {auto rgb=getRGB(i);glColor3f(rgb[0], rgb[1],rgb[2]);glRectf(0.7, 1.0*i/n-0.2,0.8, 1.0*(i+1)/n-0.2);}glFlush();// RevolveTriangle();
// glColor3f(1,0,0);
// glPointSize(10);
// glBegin(GL_POINTS);
// glVertex3d(xpos/300-1, -ypos/300+1, -1 );
// glEnd();// glGetFloatv()/******交换缓冲区,更新window上的内容******/glfwSwapBuffers(window);}glfwTerminate();return 0;
}效果展示