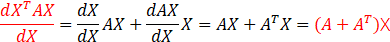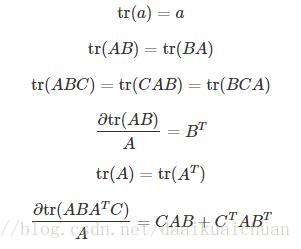参考教材可在谷歌中搜索matrix cookbook，如下图所示：

  数据按照不同的维度，可以划分为标量、向量、矩阵。所以矩阵求导可以划分为三个组，其中每组三个，共九种情况：

1. $\frac{\partial 标量}{\partial 标量}$、$\frac{\partial 标量}{\partial 向量}$、$\frac{\partial 标量}{\partial 矩阵}$

2. $\frac{\partial 向量}{\partial 标量}$、 $\frac{\partial 向量}{\partial 向量}$、 $\frac{\partial 向量}{\partial 矩阵}$

3. $\frac{\partial 矩阵}{\partial 标量}$、 $\frac{\partial 矩阵}{\partial 向量}$、 $\frac{\partial 矩阵}{\partial 矩阵}$

  分子指的是函数空间，在某些情况下为单个函数，分母指的是基向量，尤其是向量和标量的时候最容易理解。

1.分子为标量

1.1 $\frac{\partial 标量}{\partial 标量}$

  此时分子为单个函数，而基变量只有一个，所以结果也是标量。这种情况最简单。

1.2 $\frac{\partial 标量}{\partial 向量}$

  此时分子为单个函数，而基变量有多个，结果是向量。本质上就是偏导数。如果分母为行向量，则结果就为行向量。如果分母为列向量，则结果为列向量。

1.3 $\frac{\partial 标量}{\partial 矩阵}$

  此时分子为单个函数，而基变量为矩阵，结果是矩阵。具体含义不明。

2.分子为向量

2.1 $\frac{\partial 向量}{\partial 标量}$

  此时分子为函数空间，而基变量只有一个，所以结果也是向量。

2.2 $\frac{\partial 向量}{\partial 向量}$

  此时分子为函数空间，而基变量有多个，所以结果是矩阵。可以看作是标量对向量求导的扩展。这里所指的是向量和向量的求导，根据Jacobi矩阵的定义，默认指的是列向量对行向量求导。

2.3 $\frac{\partial 向量}{\partial 矩阵}$

  这里是标量对矩阵求导的扩展。但是具体物理意义不明。

3.分子为矩阵

3.1 $\frac{\partial 矩阵}{\partial 标量}$

  此时分子为矩阵函数空间，而基变量只有一个，所以结果也是矩阵。

3.2 $\frac{\partial 矩阵}{\partial 向量}$

  此时分子为矩阵函数空间，而基变量有多个，所以结果是矩阵。可以看做是向量对向量求导的扩展。

3.3 $\frac{\partial 矩阵}{\partial 矩阵}$

  这里是向量对矩阵求导的扩展。但是具体物理意义不明。

下载文档为：https://download.csdn.net/download/herosunly/11088311

矩阵运算验证网址为：http://www.matrixcalculus.org/

4. 常用求导公式

  求导不仅要满足链式法则，也要满足矩阵的乘法准则。

$$\frac{\partial }{\partial w}(A\cdot w)=A$$

$$\frac{\partial }{\partial w}(w^T\cdot A)=A^T$$

$\frac{\partial }{\partial w}(w^T\cdot A)=A^T\ne A$，为什么不等于A，而是等于$A^T$呢？

$$\frac{\partial }{\partial w}(w^T\cdot A\cdot w)=A\cdot w+A^T\cdot w$$

根据2.2的内容对上式进行简单的推导，如下所示：