1. CAS简介

比较并交换(compare and swap, CAS)，是原子操作的一种。在多线程没有锁的状态下，可以保证多个线程对同一个值的更新。

CAS可用于在多线程编程中实现不被打断的数据交换操作，从而避免多线程同时改写某一数据时由于执行顺序不确定性以及中断的不可预知性，产生的数据不一致问题。该操作通过将内存中的值与指定数据进行比较，当数值一样时将内存中的数据替换为新的值。

2. CAS的特点

1、CAS结合volatile可以实现无锁并发，适用于线程数少，多核CPU场景下。

线程数不要超过CPU核数

2、CAS是基于乐观锁实现（本身并无锁🔒，区别于synchronized）

3、CAS体现的是无锁并发、无阻塞并发

• CAS的原子性 + volatile的可见性，不断的的【比较于交换】保证线程安全
• 没有用锁🔒来保证线程安全，所以不会阻塞
• 如果竞争激烈，会导致重试频繁发生，效率下降

3. 自旋–比较和交换

自旋： 就是不停的判断比较，看能否将值交换

我们都知道，多个线程在访问共享资源的时候，会产生同步问题，所以需要加锁来保证安全。但是，一旦加了锁，同一时刻只能有一个线程获取锁对象，效率自然变低了。

那在多线程场景下，不加锁的情况下来修改值，CAS是怎么自旋的呢？

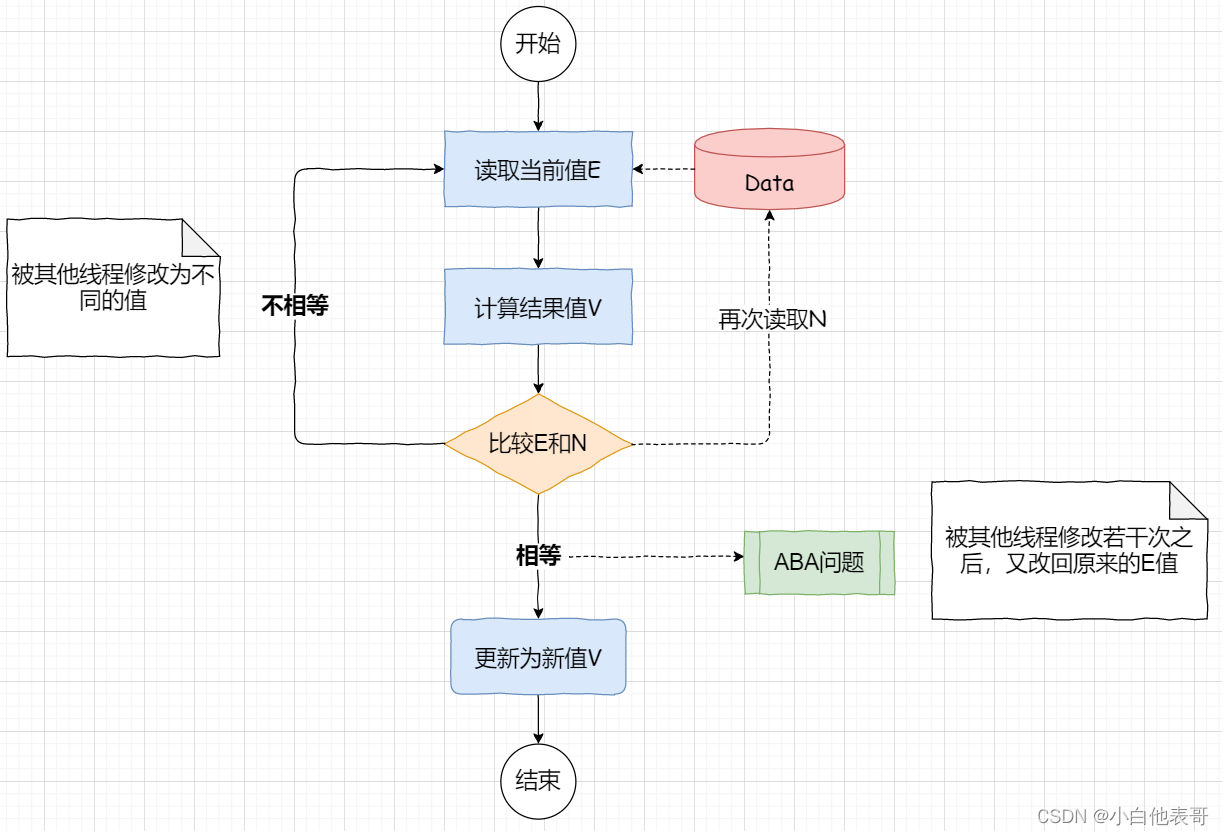
【用图举例来说明】

• 现在Data中存放的是num=0，线程A将num=0拷贝到自己的工作内存中计算（做+1操作）E=0，计算的结果为V=1
• 由于是在多线程不加锁的场景下操作，所以可能此时num会被别的线程修改为其他值。此时需要再次读取num看其是否被修改，记再次读取的值为N
• 如果被修改，即E !=N，说明被其他线程修改过。那么此时工作内存中的E已经和主存中的num不一致了，根据EMSI协议，保证安全需要重新读取num的值。直到E= N才能修改
• 如果没被修改，即E =N，说明没被其他线程修改过。那门将工作内存中的E=0改为E=1，同时写回主存。将num=0改为num=1
  为了直观的说明，再来一个经典的转账例子：

要在当前状态的余额下减10

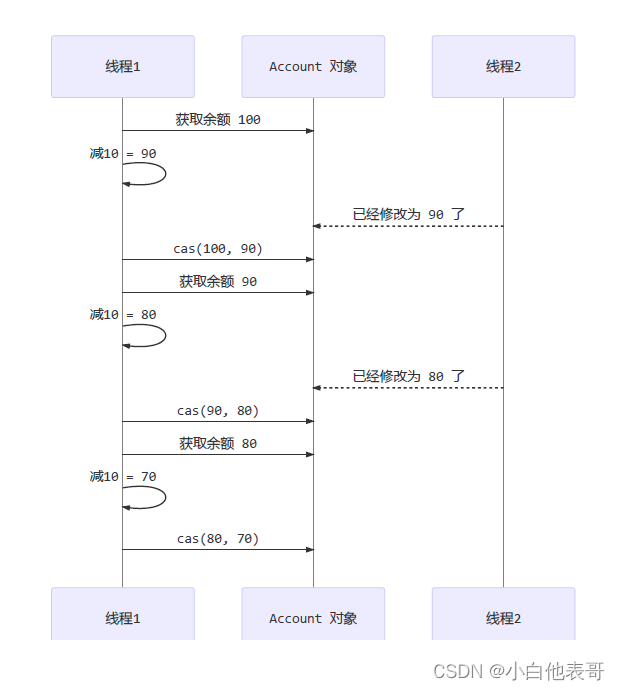
这就是自旋的比较和交换：

在多线程没有锁的状态下，可以保证多个线程访问对某一个值的更新。

4. 什么是ABA问题

举个不恰当的例子🙃。张三和他的女朋友李四分手了，经历了全球变暖以及黄金的贬值的重重考验和磨难后最终又复合。那么，在分手期间，张三是不知道李四有没有重新找过男朋友的。但是，最终的男盆友是自己就行了！这就是ABA问题。

回归到问题本身：

在线程A计算V的时候，可能线程B将num=0改为了num=2，线程C又将num=2改回了num=0(也有可能是线程B或这任意线程)。此时num的值虽然还时0，但是num已经不是一开始的num了。

用一句哲学的话来讲，就是：“世界上没有两片相同的树叶”！

5. ABA问题怎么解决

CAS是无法解决ABA问题的。解决的策略有哪些呢？

1. 添加版本号

大家在更新手机APP的时候，每次更新时软件都会有版本号。你更新完软件，还是原来的应用，但是版本号就不一样了。

同样，ABA问题也可以这样来求解。

我们把值num加一个版本号tag，当有线程修改的时候，版本号就会发生变化。在读取E的时候，同时将版本号tag也读取上，在比较E=?=N的时候，同时比较tag是否发生了改变。

2. 添加时间戳

添加世时间戳也可以解决。查询的时候把时间戳一起查出来，对的上才修改并且更新值的时候一起修改更新时间，这样也能保证，方法很多但是跟版本号都是异曲同工之妙。

6. 悲观锁

总是假设最坏的情况，每次取数据时都认为其他线程会修改，所以都会加锁（读锁、写锁、行锁等），当其他线程想要访问数据时，都需要阻塞挂起。在Java中，synchronized的思想就是悲观锁。

7. 乐观锁

总是认为不会产生并发问题，每次去取数据的时候总认为不会有其他线程对数据进行修改，因此不会上锁。

乐观锁总是认为不会产生并发问题，每次去取数据的时候总认为不会有其他线程对数据进行修改，因此不会上锁。

但是在更新时会判断其他线程在这之前有没有对数据进行修改，一般会使用版本号机制或CAS操作实现。java.util.concurrent包中借助CAS实现了区别于synchronized同步锁的一种乐观锁。

8. CAS锁升级

针对 synchronized 获取锁的方式，JVM 使用了锁升级的优化方式：

• 先使用偏向锁优先同一线程，然后再次获取锁
• 如果失败，就升级为 CAS 轻量级锁
• 如果失败就会短暂自旋，防止线程被系统挂起
• 最后如果以上都失败就升级为重量级锁
• 锁是一步步升级上去的，最初是通过很多轻量级的方式锁定的。

9. CAS的三大问题

1、ABA问题

因为CAS需要在操作值的时候，检查值有没有发生变化，比如没有发生变化则更新，但是如果一个值原来是A，变成了B，又变成了A，那么使用CAS进行检查时则会发现它的值没有发生变化，但是实际上却变化了。

解决思路:
ABA问题的解决思路就是使用版本号。在变量前面追加上版本号，每次变量更新的时候把版本号加1，那么A->B->A就会变成1A->2B->3A。

从Java 1.5开始，JDK的Atomic包里提供了一个类AtomicStampedReference来解决ABA问题。这个类的compareAndSet方法的作用是首先检查当前引用是否等于预期引用，并且检查当前标志是否等于预期标志，如果全部相等，则以原子方式将该引用和该标志的值设置为给定的更新值。

2、循环时间长开销大

自旋CAS如果长时间不成功，会给CPU带来非常大的执行开销。
如果JVM能支持处理器提供的pause指令，那么效率会有一定的提升。

pause指令有两个作用：

• 第一，它可以延迟流水线执行命令（de-pipeline），使CPU不会消耗过多的执行资源，延迟的时间取决于具体实现的版本，在一些处理器上延迟时间是零
• 第二，它可以避免在退出循环的时候因内存顺序冲突（Memory Order Violation）而引起CPU流水线被清空（CPU Pipeline Flush），从而提高CPU的执行效率。

3、只能保证一个共享变量的原子操作

当对一个共享变量执行操作时，我们可以使用循环CAS的方式来保证原子操作，但是对多个共享变量操作时，循环CAS就无法保证操作的原子性，这个时候就可以用锁。

还有一个取巧的办法，就是把多个共享变量合并成一个共享变量来操作。比如，有两个共享变量i = 2，j = a，合并一下ij = 2a，然后用CAS来操作ij。

从Java 1.5开始，JDK提供了AtomicReference类来保证引用对象之间的原子性，就可以把多个变量放在一个对象里来进行CAS操作。

原文地址:https://blog.csdn.net/weixin_43232955/article/details/107452893
https://www.jianshu.com/p/2db33f276ef8