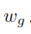1,定义
KKT是啥?
它是Karush、Kuhn和Tucker三个人。这三个人单独提出了在非线性规划中获得最优解的必要条件。
看着很复杂呀?
还好啦。。。只是将拉格朗日乘数法中的等式约束条件泛化到了不等式。
2,先来几个简单例子
为什么要搞这个看似复杂的东东?当然是为了解决一些问题。下面的问题如果你能解出来,你就可以不用学这个了。
2.1 求 f ( x 1 , x 2 ) = x 1 2 + x 2 2 的最小值,约束条件为 x 1 + x 2 = 1 和 x 2 < = α 求f(x_1,x_2)=x_1^2+x_2^2的最小值,约束条件为x_1+x_2=1和 x_2<=\alpha 求f(x1,x2)=x12+x22的最小值,约束条件为x1+x2=1和x2<=α。
易得 f ( x 1 , x 2 ) = ( 1 − x 2 ) 2 + x 2 2 = 2 ( x 2 − 0.5 ) 2 + 0.5 , f(x_1,x_2)=(1-x_2)^2+x_2^2=2(x_2-0.5)^2+0.5, f(x1,x2)=(1−x2)2+x22=2(x2−0.5)2+0.5,
则当 α > = 0.5 时, f ( x 1 , x 2 ) 在 x 2 = 0.5 处有最小值,为 0.5 \alpha>=0.5时,f(x_1,x_2)在x_2=0.5处有最小值,为0.5 α>=0.5时,f(x1,x2)在x2=0.5处有最小值,为0.5;
当 α < 0.5 , f ( x 1 , x 2 ) 在 x 2 = α 处有最小值,为 2 α 2 − 2 α + 1 \alpha<0.5,f(x_1,x_2)在x_2=\alpha处有最小值,为2\alpha^2-2\alpha+1 α<0.5,f(x1,x2)在x2=α处有最小值,为2α2−2α+1。
尴尬了。。。解出来了。。。
好吧。。用KKT的思路来玩一下吧。
先构造拉格朗日函数:
L ( x 1 , x 2 , λ , μ ) = x 1 2 + x 2 2 + λ ( x 1 + x 2 − 1 ) + μ ( x 2 − α ) \mathcal{L}(x_1,x_2,\lambda,\mu)=x_1^2+x_2^2+\lambda(x_1+x_2-1)+\mu(x_2-\alpha) L(x1,x2,λ,μ)=x12+x22+λ(x1+x2−1)+μ(x2−α)(似曾相识)
跟拉格朗日法一样对原始变量和等式约束部分求偏导数,并令其等于0:
∂ L x 1 = 2 x 1 + λ = 0 \frac{\partial\mathcal{L}}{x_1}=2x_1+\lambda=0 x1∂L=2x1+λ=0
∂ L x 2 = 2 x 2 + λ + μ = 0 \frac{\partial\mathcal{L}}{x_2}=2x_2+\lambda+\mu=0 x2∂L=2x2+λ+μ=0
∂ L λ = x 1 + x 2 − 1 = 0 \frac{\partial\mathcal{L}}{\lambda}=x_1+x_2-1=0 λ∂L=x1+x2−1=0
对于不等式部分,要用下列条件去约束:
x 2 − α < = 0 x_2-\alpha<=0 x2−α<=0
μ > = 0 \mu>=0 μ>=0
μ ( x 2 − α ) = 0 \mu(x_2-\alpha)=0 μ(x2−α)=0
容易解出:
x 1 = 1 / 2 + μ / 4 , x 2 = 1 / 2 − μ / 4 , λ = − 1 − μ / 2. x_1=1/2+\mu/4,x_2=1/2-\mu/4,\lambda=-1-\mu/2. x1=1/2+μ/4,x2=1/2−μ/4,λ=−1−μ/2.
将约束条件转化成只有 μ 和 α 的式子 \mu和\alpha的式子 μ和α的式子:
μ > = 2 − 4 α \mu>=2-4\alpha μ>=2−4α
μ > = 0 \mu>=0 μ>=0
μ ( 1 / 2 − μ / 4 − α ) = 0 \mu(1/2-\mu/4-\alpha)=0 μ(1/2−μ/4−α)=0
1),当 α > = 1 / 2 时,必须要使 μ = 0 才能满足要求,此时 x 1 = x 2 = 1 / 2 ; \alpha>=1/2时,必须要使\mu=0才能满足要求,此时x_1=x_2=1/2; α>=1/2时,必须要使μ=0才能满足要求,此时x1=x2=1/2;
2),当 α < 1 / 2 时,易得 μ > 0 ,则 μ = 2 − 4 α ,此时 x 1 = 1 − α , x 2 = α . \alpha<1/2时,易得\mu>0,则\mu=2-4\alpha,此时x_1=1-\alpha,x_2=\alpha. α<1/2时,易得μ>0,则μ=2−4α,此时x1=1−α,x2=α.
perfect,,,两种方法解出来的结果完全一样。
2.2 升级一下问题:求 f ( x 1 , x 2 , x 2 , x 4 ) = x 1 2 + x 2 2 + x 3 2 + x 4 2 的最小值,约束条件为 x 1 + x 2 + x 3 + x 4 = 1 和 x 4 < = A f(x_1,x_2,x_2,x_4)=x_1^2+x_2^2+x_3^2+x_4^2的最小值,约束条件为x_1+x_2+x_3+x_4=1和x_4<=A f(x1,x2,x2,x4)=x12+x22+x32+x42的最小值,约束条件为x1+x2+x3+x4=1和x4<=A。
思考:四个变量,这下传统的方法不好使了。。。
构造拉格朗日函数:
L ( x 1 , x 2 , λ , μ ) = x 1 2 + x 2 2 + x 3 2 + x 4 2 + λ ( x 1 + x 2 + x 3 + x 4 − 1 ) + μ ( x 4 − A ) \mathcal{L}(x_1,x_2,\lambda,\mu)=x_1^2+x_2^2+x_3^2+x_4^2+\lambda(x_1+x_2+x_3+x_4-1)+\mu(x_4-A) L(x1,x2,λ,μ)=x12+x22+x32+x42+λ(x1+x2+x3+x4−1)+μ(x4−A)
约束条件为
2 x 1 + λ = 0 2x_1+\lambda=0 2x1+λ=0
2 x 2 + λ = 0 2x_2+\lambda=0 2x2+λ=0
2 x 3 + λ = 0 2x_3+\lambda=0 2x3+λ=0
2 x 4 + λ + μ = 0 2x_4+\lambda+\mu=0 2x4+λ+μ=0
x 1 + x 2 + x 3 + x 4 = 1 x_1+x_2+x_3+x_4=1 x1+x2+x3+x4=1
x 4 < = A x_4<=A x4<=A
μ > = 0 \mu>=0 μ>=0
μ ( x 4 − A ) = 0 \mu(x_4-A)=0 μ(x4−A)=0
解得 x 1 = x 2 = x 3 = 1 / 4 + μ / 8 , x 4 = 1 / 4 − 3 / 8 μ , λ = − 1 / 2 − μ / 4 x_1=x_2=x_3=1/4+\mu/8,x_4=1/4-3/8\mu,\lambda=-1/2-\mu/4 x1=x2=x3=1/4+μ/8,x4=1/4−3/8μ,λ=−1/2−μ/4
1),当 A > = 1 / 4 时,必须要使 μ = 0 才能满足要求,此时 x 1 = x 2 = x 3 = x 4 = 1 / 4 ; A>=1/4时,必须要使\mu=0才能满足要求,此时x_1=x_2=x_3=x_4=1/4; A>=1/4时,必须要使μ=0才能满足要求,此时x1=x2=x3=x4=1/4;
2),当 α < 1 / 4 时易得 μ > 0 ,则 μ = ( 2 − 8 A ) / 3 ,此时 x 1 = x 2 = x 3 = 1 / 3 − A / 3 , x 4 = A . \alpha<1/4时易得\mu>0,则\mu=(2-8A)/3,此时x_1=x_2=x_3=1/3-A/3,x_4=A. α<1/4时易得μ>0,则μ=(2−8A)/3,此时x1=x2=x3=1/3−A/3,x4=A.
3,稍微抽象一下上述的例子
假设要求f(x)的最小值,约束条件是g(x)<=0.
用 x ∗ x^* x∗表示上述解出现时的x值。
分下面两种情况讨论上述问题:
1)假如 x ∗ x^* x∗出现在g(x)<0的范围内,则只需要满足下列条件:
d J ( x ∗ ) d x = 0 \frac{d J(x^*)}{dx}=0 dxdJ(x∗)=0
此时相当于已经解除了不等式的约束。
2)假如 x ∗ x^* x∗出现在g(x)=0处,设 x = x ∗ + δ x ,则 δ x = 0 应该是下面这种情况的解: x=x^*+\delta x,则\delta x=0应该是下面这种情况的解: x=x∗+δx,则δx=0应该是下面这种情况的解:
min δ x J ( x ∗ + δ x ) ,约束条件为 g ( x ∗ + δ x ) < = 0 \min_{\delta x} J(x^*+\delta x),约束条件为g(x^*+\delta x)<=0 minδxJ(x∗+δx),约束条件为g(x∗+δx)<=0。
用泰勒公式将上述式子改写:
min δ x [ J ( x ∗ ) + d J ( x ∗ ) δ x d x ] \min_{\delta x} [J(x^*)+\frac{d J(x^*)\delta x}{dx}] minδx[J(x∗)+dxdJ(x∗)δx],
约束条件为 g ( x ∗ ) + d g ( x ∗ ) δ x d x < = 0 g(x^*)+\frac{d g(x^*)\delta x}{dx}<=0 g(x∗)+dxdg(x∗)δx<=0
由于 J ( x ∗ ) 是个固定值且跟 δ x 无关,且 g ( x ∗ ) = 0 ,所以上述条件可以进一步简化为 J(x^*)是个固定值且跟\delta x无关,且g(x^*)=0,所以上述条件可以进一步简化为 J(x∗)是个固定值且跟δx无关,且g(x∗)=0,所以上述条件可以进一步简化为:
min δ x d J ( x ∗ ) δ x d x \min_{\delta x} \frac{d J(x^*)\delta x}{dx} minδxdxdJ(x∗)δx,
约束条件为 d g ( x ∗ ) δ x d x < = 0 \frac{d g(x^*)\delta x}{dx}<=0 dxdg(x∗)δx<=0。
上述问题可以看成是关于 δ x \delta x δx的线性规划问题。分下列几种情况:

我们需要使 δ x = 0 \delta x=0 δx=0成为上述情况的解,因此case 2和case 3满足条件,即需要一个正数 μ \mu μ使得:
d J ( x ∗ ) d x + μ d g ( x ∗ ) d x \frac{d J(x^*)}{dx}+\mu\frac{d g(x^*)}{dx} dxdJ(x∗)+μdxdg(x∗)成立。
4,正式给出KKT条件
假设要优化f(x),即求最大值或最小值,约束条件为:
1)不等式约束: g i ( x ) < = 0 , i = 1 , 2 , . . . , m g_i(x)<=0,i=1,2,...,m gi(x)<=0,i=1,2,...,m
2)等式约束: h j ( x ) = 0 , j = 1 , 2 , . . . , ℓ h_j(x)=0,j=1,2,...,\ell hj(x)=0,j=1,2,...,ℓ
假设f(x)、g(x)和h(x)在点 x ∗ x^* x∗都是可以连续微分的,则存在常量 μ i ( i = 1 , 2 , . . . , m ) 和 λ j ( j = 1 , 2 , . . . , ℓ ) \mu_i(i=1,2,...,m)和\lambda_j(j=1,2,...,\ell) μi(i=1,2,...,m)和λj(j=1,2,...,ℓ)满足下面四个条件:
1,定常方程式

2,原始可行性
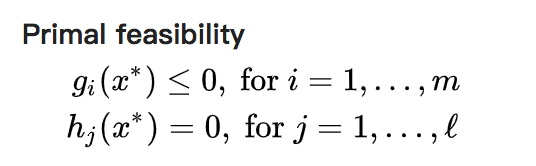
3,对偶可行性
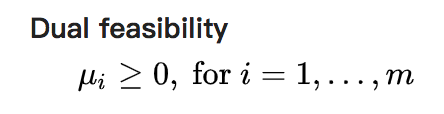
4,互补松弛性
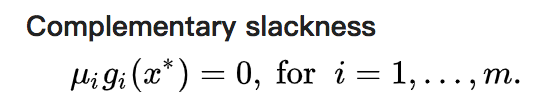
当m=0,即不存在不等方程时,KKT条件变成了拉格朗日条件,KKT乘子变成了拉格朗日乘子。
Reference
https://zhuanlan.zhihu.com/p/38163970
https://ccjou.wordpress.com/2017/02/07/karush-kuhn-tucker-kkt-%E6%A2%9D%E4%BB%B6/