基础知识

可执行文件

计算机中可以被直接执行的程序被称之为可执行文件，可执行文件中是由指定操作系统的可执行文件格式规范与当前CPU机器指令码组成。不同的操作系统、不同的CPU之间的可执行文件都可能存在或多或少的差异。本篇主要以Windows操作系统、x86架构的CPU进行参考。

Windows中的可执行文件格式被称之为PE文件格式。是向操作系统描述程序该如何被加载，CPU指令从文件何处执行，需要给程序分配多少内存空间，以及空间如何布局等。如图1.1

[图1.1 使用Petools工具分析PE文件信息]

可执行文件的生成

构造这种文件需要编译器，曾经的开发者通过直接面向CPU机器指令编程，使用的是的汇编语言，通过汇编器生成可执行文件。随着开发应用程序的功能逐渐复杂，汇编语言的效率显得十分低下。开发者们希望有这么一个程序，这个程序可以把人们常用的语句翻译成一条或多条汇编语句，至此C语言的编译器就诞生了。如此下来人们只需要写遵循指定语法的人类语言，C语言编译器可以将其转换为对应功能的汇编代码。随后通过汇编器将其转换为CPU能够直接执行的机器码。如图 1.2。

[图1.2 使用VS2019显示C语言汇编]

何为逆向

逆向是为了逆转这个过程，通过分析汇编代码还原程序逻辑从而获得程序某处的设计。我们可以很轻松的拿到程序执行的汇编代码，因为它们与CPU机器码是一一对应的。虽然ida有将其转换为C代码的能力，但这依赖于IDA自身的推测分析，轻度的针对性混淆就可以导致ida无法推测出代码的意图从而转换C代码失败。所以我们有必要学会简单的汇编和C语言与汇编转换的某些固定约定,以便对抗一些指令混淆行为。在此之前需要有一定的C语言基础知识，大概需要了解到指针左右。

C语言--数据存储格式

变量

变量——用于标识和存储计算结果的概念。不同类型的变量有着不同的存储空间大小和存储的格式。

整数

对于char到long long都是有符号整数的存储方式，其最高位为符号位，其余位表示数字。区别是其能够存放的数值大小不同，如图 2.1,2.2。

char 只能存放一个字节，主要用来存放文字编码。long long为8个字节，用来存放大数字。

[图2.1 整型对应大小]

[图2.2 整型存储格式]

无符号（unsigned ）的存储格式则是将符号位也用来存放二进制数字，如图2.3。

[图2.3 无符号整型存储格式]

在不同的CPU中存储与解析数据的模式分为两种——大端模式与小端模式

大端模式下：总是将数值中最高位的字节存在前面，最低位的字节存在后面

小端模式下：总是将数值中最低位的字节存在前面，最高位的字节存在后面

[图 2.4 大小端模式存储0x11223344]

我们常用的8086 系列芯片就是小端模式，小端模式有个好处：类型转化时无需重新组合，只需要向后延申00。因为44 33 22 11 00 00 00 00同样标识0x11223344，而大端的11 22 33 44需要按需向后移动00 00 00 00 11 22 33 44.

浮点数

浮点数的存储格式相对较为复杂，它与科学计数法类似，相当于2进制的科学计数法。格式如图 2.5

[图 2.5 浮点数的数据格式]

S: 符号位，为0是非负数，为1是负数

E: 二进制指数位

M: 二进制尾数位

10进制的科学计数法是将数值控制在1~10之间，算法如下：

1234.5678 = 1234.5678 * 10^0

= (1234.5678 / 10)*10^1

= (123.45678 / 10 )*10^2

以此类推，直到

1.2345678 * 10^3

2进制与10进制类似

1234.5678 = 1234.5678 * 2 ^ 0

= (1234.5678 / 2)*2^1

= (617.2839 / 2)*2^2

以此类推，直到小数点开头数字<2 且>1。

= 1.2056326171875 * 2^10

得出指数位 10 （十进制）

但有一点区别，2进制不能够表示像1.20563... 十进制的小数。因此需要些算法。

0.2056326171875 （舍去开头的1）

0.2056326171875 * 2 >= 1 ... 0

0.411265234375 * 2 >= 1   ... 0

0.82253046875 * 2 >= 1   ... 1

0.6450609375 * 2 >= 1 ... 1

0.290121875 * 2 >= 1 ... 0

0.58024375 * 2 >= 1 ... 1

0.1604875 * 2 >= 1 ... 0

0.320975 * 2>= 1 ... 0

0.64195 * 2 >= 1 ... 1

0.2839 * 2 >= 1 ... 0

0.5678 * 2 >= 1 ... 1

0.1356 * 2 >= 1 ... 0

0.2712 * 2 >= 1 ... 0

0.5424 * 2 >= 1 ... 1

0.0848 * 2 >= 1 ... 0

0.1696 * 2 >= 1 ... 0

0.3392 * 2 >= 1 ... 0

0.6784 * 2 >= 1 ... 1

.....

得出52位的二进制尾数0011010010100100010101101101010111001111101010101101

得出的十进制指数位 10

指数位为了兼容负指数的存在需要进行简单的运算, 参考图2.6。

[图 2.6 浮点数指数的存储格式]

10+127 = 137 ==转二进制==> 10001001

将其按照图 2.5描述进行拼接得出二进制数值：

float: 0|10001001|00110100101001000101011 ==HEX=> 449A522B

double: 0|10000001001|0011010010100100010101101101010111001111101010101101

==HEX=> 40934A456D5CFAAD

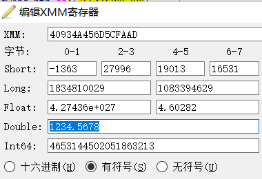
[图 2.7 double类型存储1234.5678]

结构体

结构体无非是将内部所有的成员叠加在一起存储。如图 2.8:

[图 2.8 结构体的存储格式]

他们虽然是叠在一起的，但是并没有紧贴在一起，像是以某种特殊的形式布局——内存对齐机制。

因为每一次内存请求都是对齐的，可能是4或者8或者其他偏移与大小取出内存数值，内存对齐机制为了能够仅一次访问内存就取出需要的所有数据，减少不必要的多次内存访问以牺牲存储空间来提高读取效率。

内存不对齐访问如图 2.9所示，需要不必要的多次访问内存。

[图 2.9 不对齐内存访问]

对于内存对齐的规则很简单：变量存储起始地址必须是存储大小的整倍数。

如上图 2.7 结构中的b成员，其大小为2但上个成员后偏移为1，这时需要对齐2字节，则b成员的起始地址需要从2开始大小为2。

结构中的e成员，其大小为8但上个成员后偏移为12，这时需要对齐8字节，则b成员的起始地址需要从16开始大小为8。