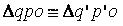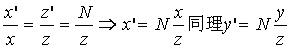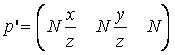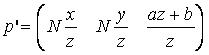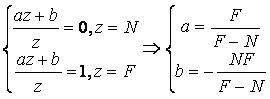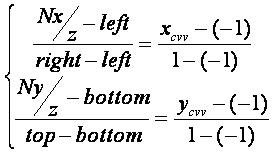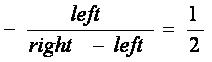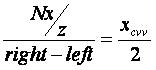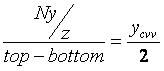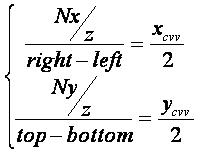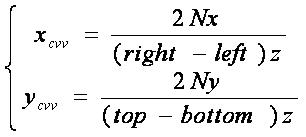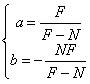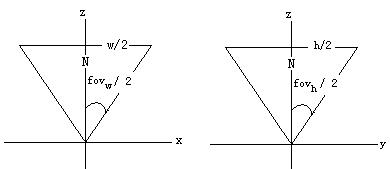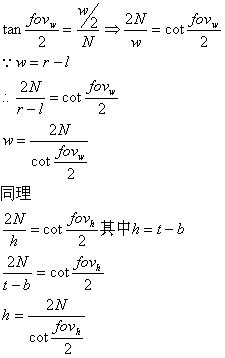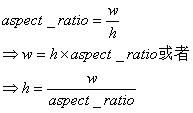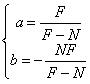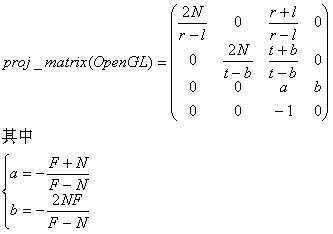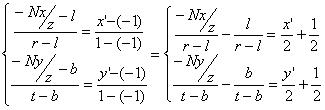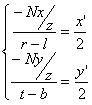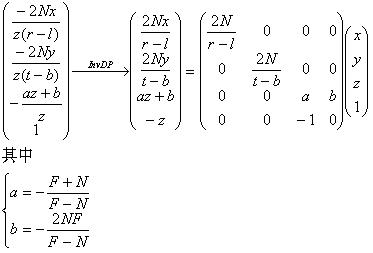-潘宏

-2009.4.14

-本人水平有限，疏忽错误在所难免，还请各位数学高手、编程高手不吝赐教

-email: popyy@netease.com

-B站专栏： https://b23.tv/oWsl6PD

 

 

在上一篇文章中我们讨论了透视投影变换的原理，分析了OpenGL所使用的透视投影矩阵的生成方法。正如我们所说，不同的图形API因为左右手坐标系、行向量列向量矩阵以及变换范围等等的不同导致了矩阵的差异，可以有几十个不同的透视投影矩阵，但它们的原理大同小异。这次我们准备讨论一下Direct3D（以下简称D3D）以及J2ME平台上的JSR184（M3G）（以下简称M3G）的透视投影矩阵，主要出于以下几个目的：

 

（1）       我们在写图形引擎的时候需要采用不同的图形API实现，当前主要是OpenGL和D3D。虽然二者的推导极为相似，但D3D的自身特点导致了一些地方仍然需要澄清。

（2）       DirectX SDK的手册中有关于透视投影矩阵的一些说明，但并不详细，甚至有一些错误，从而使初学者理解起来变得困难，而这正是本文写作的目的。

（3）       M3G是J2ME平台上的3D开发包，采用了OpenGL作为底层标准进行封装。它的透视投影矩阵使用OpenGL的环境但又进行了简化，值得一提。

 

本文努力让读者清楚地了解D3D与M3G透视投影矩阵的原理，从而能够知道它与OpenGL的一些差别，为构建跨API的图形引擎打好基础。需要指出的一点是为了完全理解本文的内容，请读者先理解上一篇文章《深入探索透视投影变换》的内容，因为OpenGL和它们的透视投影矩阵的原理非常相似，因此这里不会像上一篇文章从基础知识讲起，而是对比它们的差异来推导变换矩阵。我们开始！

 

OpenGL与D3D的基本差异

前面提到，不同API的基本差异导致了最终变换矩阵的不同，而导致OpenGL和D3D的透视投影矩阵不同的原因有以下几个：

 

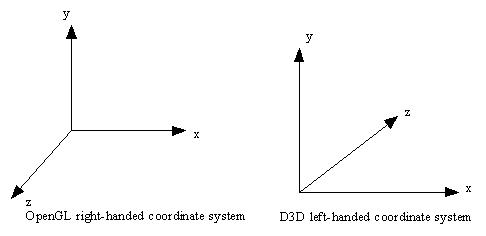
（1）       OpenGL默认使用右手坐标系，而D3D 默认使用左手坐标系。

 

 

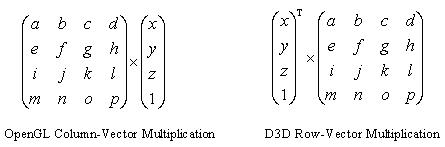
（2）       OpenGL使用列向量矩阵乘法而D3D使用行向量矩阵乘法。

 

 

 

（3）       OpenGL的CVV的Z范围是[-1, 1]，D3D的CVV的Z范围是[0, 1]。

 

 

    以上这些差异导致了最终OpenGL和D3D的透视投影矩阵的不同。

 

D3D的透视投影矩阵推导

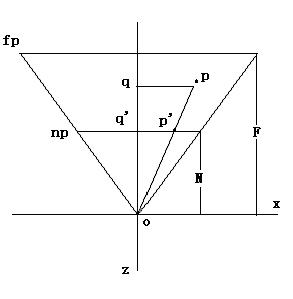
我们先来看最最基本的透视关系图（上一篇文章开始的时候使用的图）：

 

这里我们考察的是xz平面上的关系，yz平面上的关系同理。这里o是相机位置。np是近裁剪平面，也是投影平面，N是它到相机的距离。fp是远裁剪平面，F是它到相机的位置。p是需要投影的点，p’是投影之后的点。根据相似三角形定理，我们有

 

 

则有

 

 

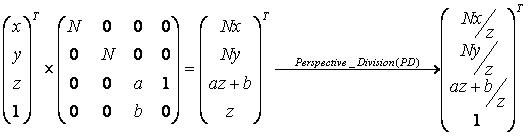
注意到OpenGL使用右手坐标系，因此应该使用-N（请参考上一篇文章的这一步），而D3D使用左手坐标系，因此使用N，这是二者的不同点之一。这样，我们得到投影之后的点

 

第三个信息点是变换之后的z在投影平面上的位置，也就是N，它已经没用了，我们把p’写成

 

从而用第三个没用信息点它来存储z（如果读者对这一点不太了解，请参考上一篇文章）。接下来我们求出a和b，从而在z方向上构建CVV。请注意这里是OpenGL和D3D的另一个不同点，OpenGL的CVV的z范围是[-1, 1]，而D3D的CVV的z范围是[0, 1]。也就是说，D3D 中在近裁剪平面上的点投影之后的点会处于CVV的z=0平面上，而在远裁剪平面上的点投影之后的点会在CVV的z=1平面上。这样我们的计算方程就是

 

 

 

从而我们得到了透视投影矩阵的第一个版本

 

 

即

 

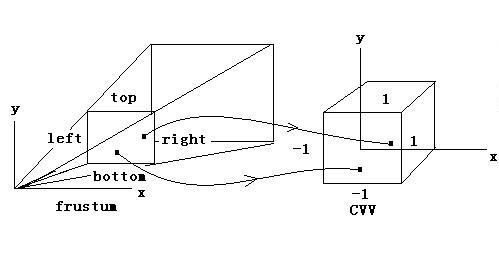
这个时候第三个分量变换到CVV情形了，CVV的z范围是[0,1]。接下来根据上一篇文章所讲到的，我们要把前两个分量变成CVV情形，CVV的x和y范围是[-1, 1]，如下图所示：

 

使用线性插值，我们有：

 

 

这里left和right是投影平面的左右范围，top和bottom是投影平面的上下范围。xcvv和ycvv是我们需要算出的在CVV情形中的x和y，也就是我们要计算出的结果。但在算出它们之前，我们先把上面的式子写成：

 

 

这里有一个需要注意的地方，如果投影平面在x方向上居中，则

 

 

 

那么第一个式子就可以销掉等号两边的1/2，写成

 

 

同理，如果投影平面在y方向上居中，则第二个式子可以写成

 

 

则我们现在分两种情况讨论：

（1）       投影平面的中心和x-y平面的中心重合（在x和y方向上都居中）

（2）       一般情况

我们分别讨论：

 

（1）特殊情况方程

 

 

这组是特殊情况，方程比较简单，但也是使用频率最高的方式（这是D3DXMatrixPerspectiveLH、D3DXMatrixPerspectiveRH、D3DXMatrixPerspectiveFovLH、D3DXMatrixPerspectiveFovRH四个方法所使用的情况）。我们导出它：

 

 

则我们反推出透视投影矩阵：

 

 

其中

 

 

而r-l和t-b可以分别看作是投影平面的宽w和高h。最后那个矩阵就是D3D的透视投影矩阵之一。另外呢，如果我们不知道right、left、top以及bottom这几个参量，也可以根据视野（FOV – Field Of View）参量来求得。下面是两个平面的视野关系图：

 

 

 

  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

其中，两个fov分别是在x-z以及y-z平面上的视野。如果只给了一个视野，也可以通过投影平面的宽高比计算出来：

 

用一个视野算出w或者h，然后用宽高比算出h或者w。

 

（2）一般情况的方程

 

 

 

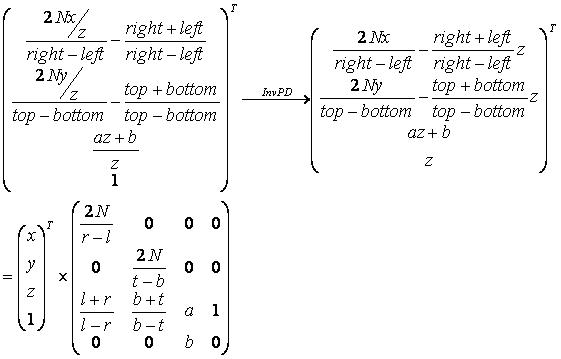
这组方程比较繁琐，但更具一般性（和OpenGL一般矩阵的推导一致，这也是D3DXMatrixPerspectiveOffCenterLH和D3DXMatrixPerspectiveOffCenterRH两个方法所使用的情况）。我们导出它：

 

 

 

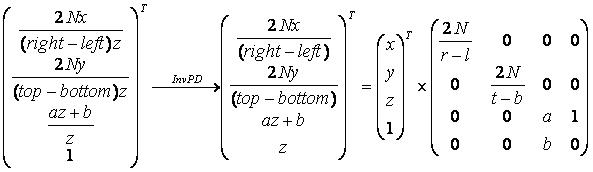
我们继续反推出透视投影矩阵：

 

其中

 

最后那个矩阵就是D3D的一般透视投影矩阵。

 

好了，目前为止，我们已经导出了D3D的两个透视投影矩阵。下面我把上一篇导出的OpenGL的透视投影矩阵写出来，大家可以拿它和刚刚导出的D3D的一般性透视投影矩阵做一个对比。

 

如果仔细观察，可以发现二者在元素的布局上是一个转置的关系，这个就是由它们使用的左右手坐标系以及使用的行列矩阵的差异造成的。而另外在一些元素的细节上也存在着差异，这是由于D3D的CVV的z范围不同造成的。可见在原理相同的情况下，细微的环境差异可以造成非常大的变化，而这就是透视投影矩阵存在诸多不同版本的原因。一般情况的透视投影矩阵也可以使用视野方式来定义，方法和特殊情况相同。

M3G的透视投影矩阵

M3G是对OpenGL进行的一个封装，它的透视投影变换矩阵被放到了类Camera里面。因为它封装了OpenGL，因此环境和OpenGL相同：右手坐标系、列向量乘法、CVV范围[-1， 1]。它唯一和OpenGL有些差异的地方就在于它只使用投影平面的中心和x-y平面的中心重合（在x和y方向上都居中）的情况（就是我们上面D3D的第一种特殊情况）。我们用OpenGL透视投影矩阵最终版本来说明（再次提醒，如果读者对此感到迷惑，请参考第一篇文章）：

 

 

上面是OpenGL透视投影矩阵的最终版本，也是一般性版本，我们要把它变成特殊性，版本，非常简单，和上面D3D的特殊情况一样，我们从对x和y进行插值的那一步来看：

 

 

和D3D的第一种情况一样，销掉两边的1/2，得到：

 

 

则我们反推出透视投影矩阵：

 

 

最右边那个矩阵就是M3G的透视投影矩阵。仍然可以通过视野参数来设置透视投影矩阵，这里请读者自行推导，方法与上面D3D的完全相同。

 

结束语

    我们已经完成了对D3D和M3G透视投影矩阵的说明。如果读者理解了上面的内容，可能会觉得有些厌恶——为什么没有一个统一的标准，在同一个原理下为什么要弄出这么多种差别？原因有很多，历史遗留问题、API厂商之间的问题等等。但对于我们来说，抓住了原理以及方法，不论如何变化都应该不会迷失。下次见！