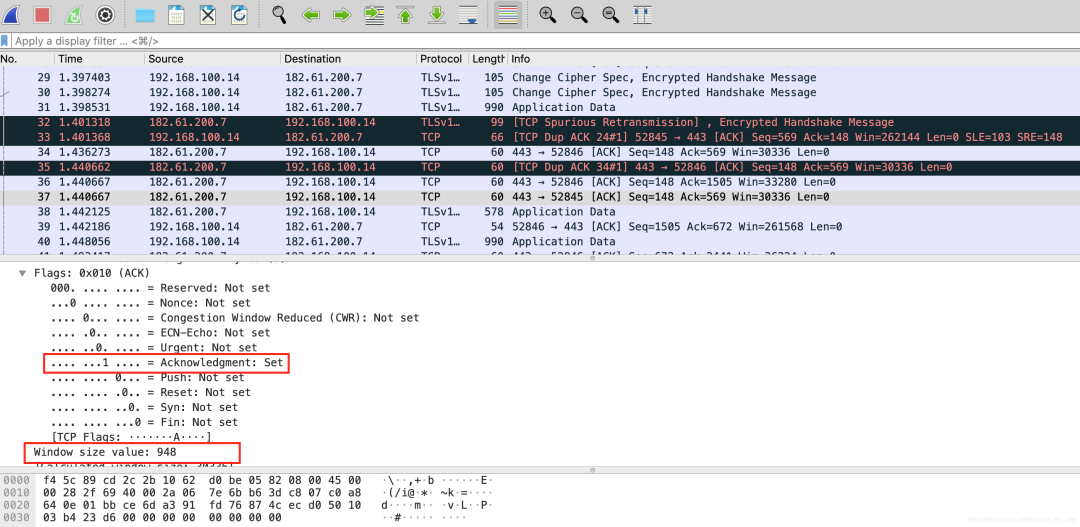
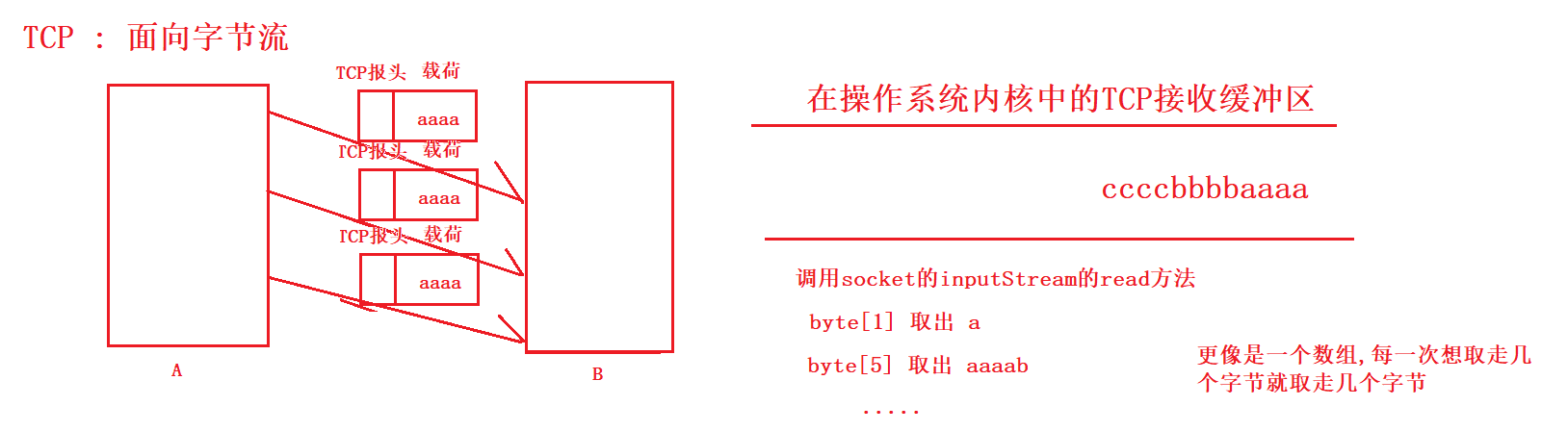
一般来说，我们总是希望数据传输得更快一些。但是如果发送方发送的更快，接收方就可能来不及接收，这就会造成数据的丢失。所谓流量控制就是让发送方的发送速率不要太快，要让接收方来得及接收。
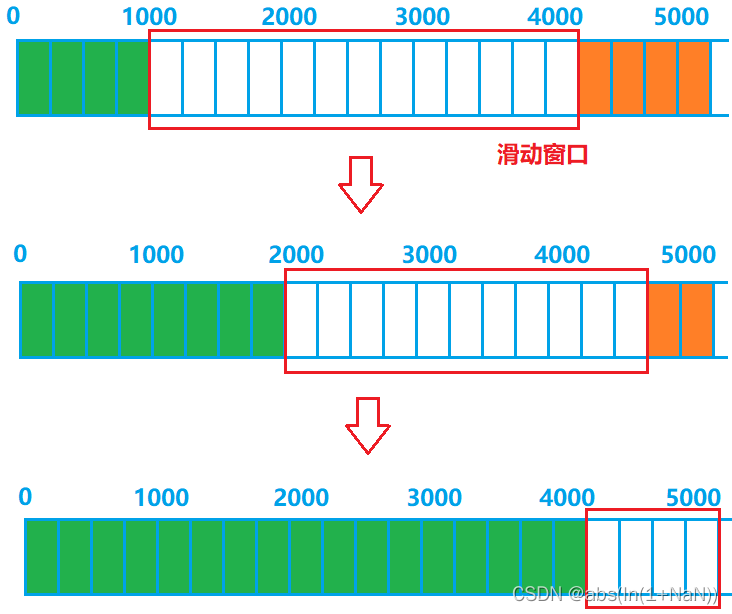
滑动窗口就是用于实现流量控制的。可以看到下面关于滑动窗口进行流量控制的例子：

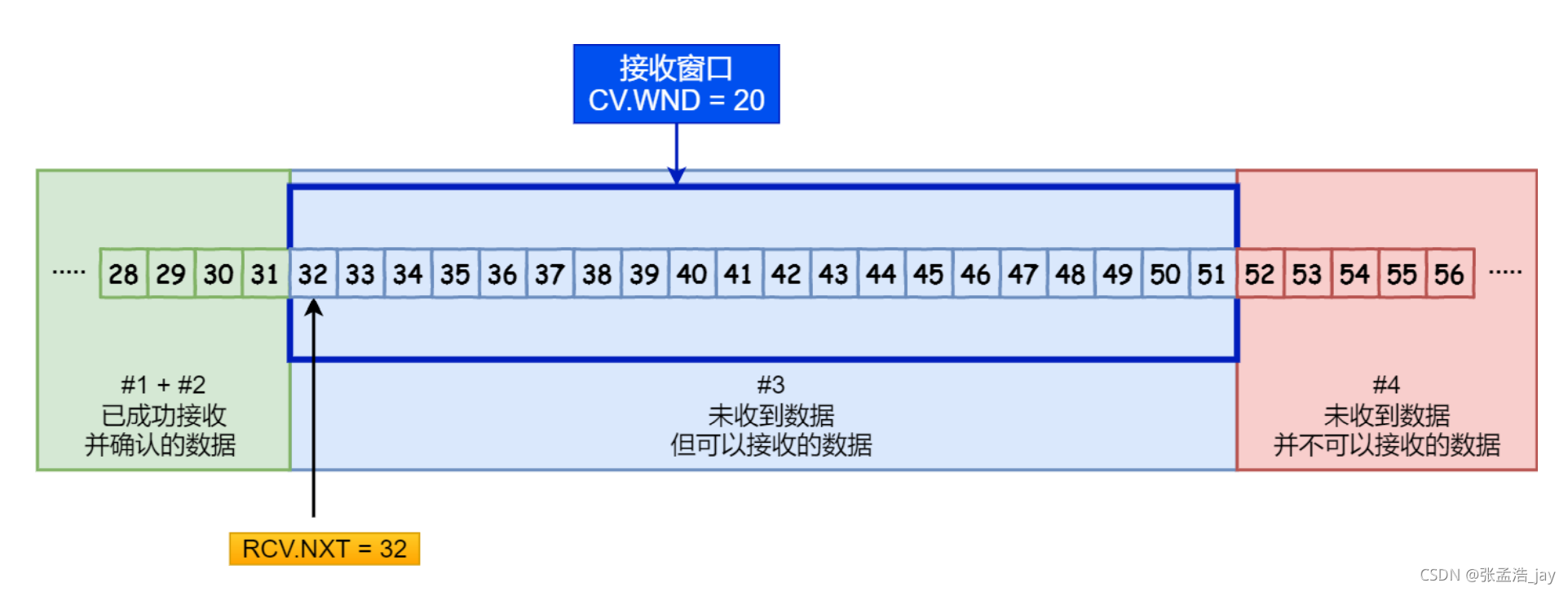
上图中，A作为发送端，B作为接收端，当A发送了三个数据报的时候（第三个数据报丢失），每个数据报100字节的长度，B做出了第一次流量控制，通过返回的rwnd（receiver window）接收窗口的大小为300字节，也就是告诉发送端还能再发送300个字节的大小，由于201-300字节的数据暂时未收到，所以ack=201，也就是期望下一次收到的起始字节序号为201，一直到500.并且ACK置为1，说明是确认收到，此时的确认号字段ack才有意义。
同理，后面还有两次流量控制，在每一次接收方发送数据报到接收方的时候，都会有这么三个关键字段的信息，一个是确认ACK，置为1的时候确认号字段才有效。第二个是确认号字段ack，说明希望收到的下一个数据报的起始字节序号。第三个rwnd，说明接收方还能发送的一个数据段字节的范围。

考虑一种特殊情况：假如接收方发送了rwnd=0的数据报给发送方（可能因为暂无缓存空间可以接收），但是之后有了多余的缓存空间，还想再接收来自发送方的数据。那么B给A发rwnd=400的数据报，但是这个数据报恰好在传输过程中丢失了，这个时候A在等B的非零窗口的通知，B在等A发送的数据，这样的话相互等待，形成了死锁的局面。
解决办法是：TCP为每个连接设有一个持续计时器，只要A收到了零窗口的通知，就启动了这个持续计时器，时间到期，A就给B发送一个零窗口探测报文段，B就可以给A发送一个窗口值，如果依旧为0，那么重新设置持续计时器，如果不是0，死锁的局面被打破，A就可以发送数据了。
我的理解：因为建立了TCP连接，大多数时候总是要发送数据的，要不然就可以关闭连接了，所以哪怕有时候接收方设置接收窗口为0，那很多时候都是由于没有缓存过于拥挤，所以发送方有理由相信不过一会就可以让它发送信息了，因为如上面的情况一样，可能准备让发送方发送数据的报文恰好丢失了。

参考书籍：《计算机网络（第七版）》谢希仁